مشتق تابع های مثلثاتی معکوس: انتگرال های مربوط
در این مقاله فرمول های متداول مشتقات توابع مثلثاتی معکوس را درجدول زیر عرضه می کنیم و نشان می دهیم که چگونه به دست می آیند،و درباره فرمول های انتگرال های نظیر بحث می کنیم. خواهیم دید که محدودیت هایی که دامنه های توابع مثلثاتی معکوس دارند، به طور طبیعی، محدودیت هایی برای دامنه مشتقات نیز هستند.

 مثال1 الف)
مثال1 الف)
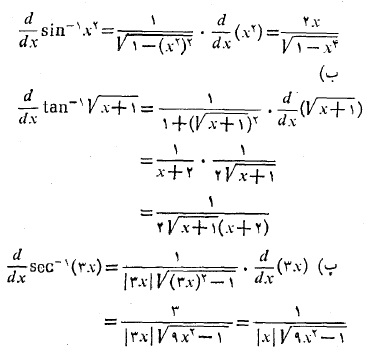
برای اینکه نشان دهیم چگونه فرمول های مشتق های فوق به دست می آیند، فرمول های 1و 5 جدول را اثبات می کنیم.

مشتقy=sin-1u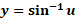
می دانیم که تابع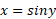 در بازه باز
در بازه باز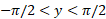 مشتق پذیر است و مشتقش، کسینوس،در این بازه مثبت است. بنابراین قاعده 11 درمقاله قبلبه ما این اظمینان را می دهد که تابع معکوس
مشتق پذیر است و مشتقش، کسینوس،در این بازه مثبت است. بنابراین قاعده 11 درمقاله قبلبه ما این اظمینان را می دهد که تابع معکوس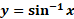 ،در سراسر بازه
،در سراسر بازه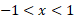 مشتق پذیر است. با وجود این نمی توانیم انتظار داشته باشیم که این تابع در
مشتق پذیر است. با وجود این نمی توانیم انتظار داشته باشیم که این تابع در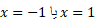 مشتق پذیر باشد،زیرا در این نقاط خط های مماس بر نمودار، قائم اند.
مشتق پذیر باشد،زیرا در این نقاط خط های مماس بر نمودار، قائم اند.
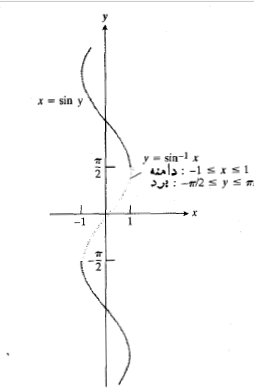
برای محاسبه مشتق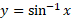 ، از دو طرف رابطه
، از دو طرف رابطه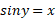 نسبت به
نسبت به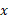 مشتق می گیریم
مشتق می گیریم
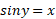

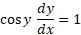
حال دو طرف را بر 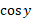 (که برای
(که برای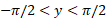 مثبت است) تقسیم می کنیم
مثبت است) تقسیم می کنیم
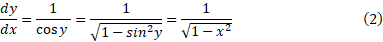
مشتق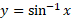 نسبت به
نسبت به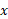 عبارت است از
عبارت است از
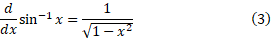
اگرu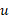 تابع مشتق پذیری ازx
تابع مشتق پذیری ازx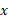 باشد، قاعده زنجیری را به صورت
باشد، قاعده زنجیری را به صورت
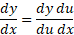
در مورد 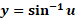 به کار می بندیم و نتیجه می گیریم که
به کار می بندیم و نتیجه می گیریم که
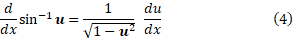
مشتق
ابتدا از دو طرف رابطه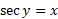 نسبت به
نسبت به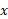 مشتق می گیریم
مشتق می گیریم
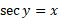

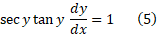
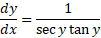
برای بیان نتیجه حاصل بر حسب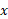 ، از روابط زیر استفاده می کنیم
، از روابط زیر استفاده می کنیم
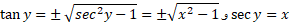
پس
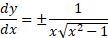
با علامت چه بکنیم؟ نگاهی به شکل زیر نشان می دهد که شیب نمودار همیشه مثبت است.
همیشه مثبت است.
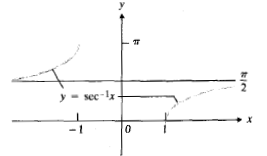
پس

با استفاده از قدر مطلق، معادله (6) به صورت تک معادله زیر در می آید
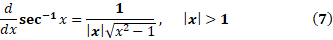
حال از قاعده زنجیری استفاده می کنیم و نتیجه می گیریم
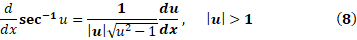
که در آن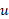 تابع مشتق پذیری از
تابع مشتق پذیری از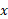 است.
است.
فرمول های انتگرال گیری
ممکن است انتظار داشته باشید که از شش فرمولمشتق در جدوا فوق شش فرمول انتگرال گیری جدید به دست آید؛ اما تنها سه تای آن ها مهم اند.
انتگرال هایی که توابع مثلثاتی معکوس منجر می شوند
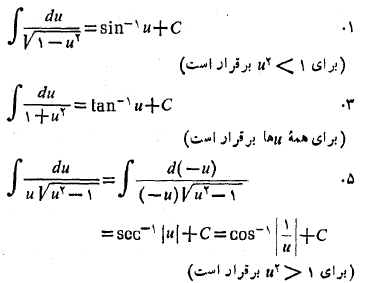
سه تای دیگر مطلب تازه ای در بر ندارند
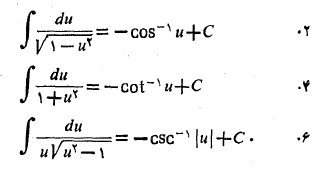
 مثال2 مطلوب است محاسبه
مثال2 مطلوب است محاسبه
الف)
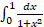 و
و
ب) 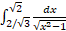
حل: الف)
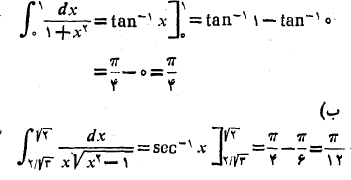
اگر فورا نمی توانید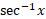 را به ازای حدودانتگرال گیری محاسبه کنید، مثلث هایی شبیه شکل زیر رسم کنید.
را به ازای حدودانتگرال گیری محاسبه کنید، مثلث هایی شبیه شکل زیر رسم کنید.
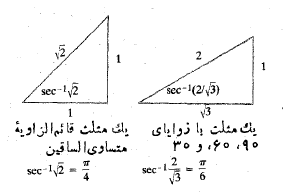
 مثال3 مطلوب است محاسبه
مثال3 مطلوب است محاسبه
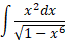
حل: شباهت بین انتگرال مفروض و صورت متداول
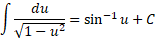
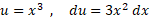
را به ذهن القا می کند. به این ترتیب
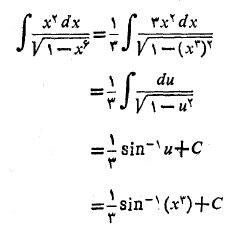
 مثال4 مطلوب است محاسبه
مثال4 مطلوب است محاسبه
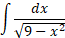
حل: این همانانتگرال آرک سینوس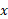 است که در آن، 9 جای 1 را گرفته است. برای اینکه به جای 9، 1 قرار گیرد، از
است که در آن، 9 جای 1 را گرفته است. برای اینکه به جای 9، 1 قرار گیرد، از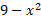 ، از 9 فاکتور می گیریم و آن را پس از جذر گرفتن به بیرون رادیکال منتقل می کنیم
، از 9 فاکتور می گیریم و آن را پس از جذر گرفتن به بیرون رادیکال منتقل می کنیم
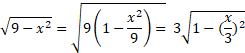
توجه کنید که به جای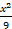 نوشته ایم
نوشته ایم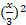 . لذا
. لذا
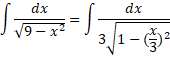
حال جانشانی های
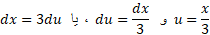
را به کار می گیریم. بنابراین
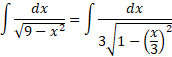
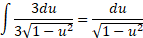

لگاریتم طبیعی و مشتق آن
لگاریتم طبیعی یک عدد مثبت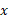 که با
که با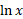 نمایش داده می شود، بنا به تعریف، مقدار انتگرال تابع
نمایش داده می شود، بنا به تعریف، مقدار انتگرال تابع 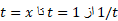 است.
است.
تعریف لگاریتم طبیعی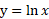
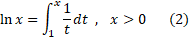
به ازای هر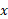 بزرگتر از 1، این انتگرال مساحت ناحیه ای را نشان می دهد که از بالا به خم
بزرگتر از 1، این انتگرال مساحت ناحیه ای را نشان می دهد که از بالا به خم 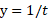 ، از پایین به محور
، از پایین به محور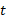 ، از طرف چپ به خط
، از طرف چپ به خط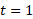 ، و از طرف راست به خط
، و از طرف راست به خط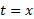 محدود است.
محدود است.
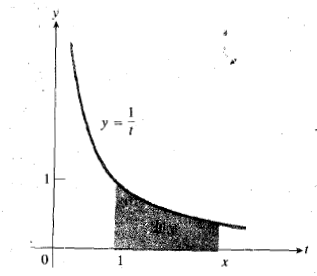
اگر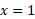 ، مرزهای چپ و راست ناحیه بر هم منطبق می شوند، و لذامساخت صفر است
، مرزهای چپ و راست ناحیه بر هم منطبق می شوند، و لذامساخت صفر است
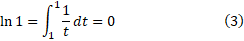
اگر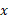 کوچکتراز یک باشد، آنگاه مرز چپ، خط
کوچکتراز یک باشد، آنگاه مرز چپ، خط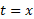 و مرز راست،
و مرز راست،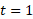 است. در این حالت
است. در این حالت
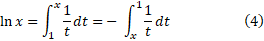
برابر است با منهایمساحت زیر خم بین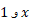 . مقدارانتگرال معین در (2) را می توانیم به کمک قاعده سیمپسون تا هر چند رقم اعشاری که بخواهیم بدست آوریم.
. مقدارانتگرال معین در (2) را می توانیم به کمک قاعده سیمپسون تا هر چند رقم اعشاری که بخواهیم بدست آوریم.
چون تابع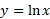 با انتگرال
با انتگرال
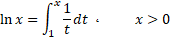
تعریف می شود، فورا از نخستینقضیه اساسی دیفرانسیل و انتگرال نتیجه می شود که

اگر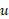 تابع مشتق پذیری از
تابع مشتق پذیری از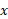 باشد، آنگاه از قاعده زنجیری
باشد، آنگاه از قاعده زنجیری
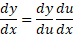
فرمول کلی تر زیر به دست می آید

 مثال1 اگر
مثال1 اگر را بیابید
را بیابید
حل:
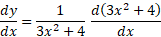
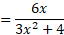
انتگرال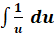
فرمول انتگرال
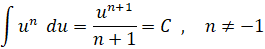
شامل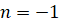 نمی شود، زیرا مشتق هیچ توانی از
نمی شود، زیرا مشتق هیچ توانی از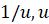 نیست. حال در موقعیتی قرار داریم که به حالت استثنا بپردازیم، زیرا معادله(6) فورا به معادله
نیست. حال در موقعیتی قرار داریم که به حالت استثنا بپردازیم، زیرا معادله(6) فورا به معادله
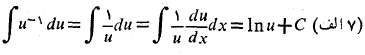
منجر می شود، با این شرط که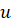 مثبت باشد. اما اگر
مثبت باشد. اما اگر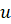 منفی باشد، آنگاه
منفی باشد، آنگاه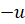 مثبت است و
مثبت است و
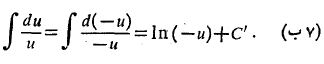
دو نتیجه (7 الف) و (7 ب) را می توان در یک نتیجه واحد به صورت زیر تلفیق کرد.
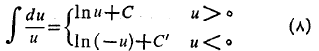
اگر علامت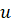 در دامنه مفروضش تغییر نکند، آنگاه یک مقدار ثابت انتگرال گیری کافی است، و ازفرمول زیر می توان استفاده کرد.
در دامنه مفروضش تغییر نکند، آنگاه یک مقدار ثابت انتگرال گیری کافی است، و ازفرمول زیر می توان استفاده کرد.
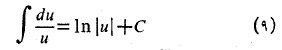
در کاربردها باید به خاطر داشت که دراینجا تابع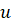 می تواند هر تابع مشتق پذیر
می تواند هر تابع مشتق پذیر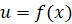 باشد. معادله(9) حاکی است که انتگرال هایی با یک صورت خاص، به لگاریتم منجر می شوند. یعنی اگر
باشد. معادله(9) حاکی است که انتگرال هایی با یک صورت خاص، به لگاریتم منجر می شوند. یعنی اگر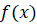 تابع مشتق پذیری باشد که بر دامنه مفروضش تغییر علامت ندهد، آنگاه
تابع مشتق پذیری باشد که بر دامنه مفروضش تغییر علامت ندهد، آنگاه
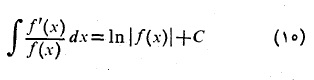
 مثال2 مطلوب است محاسبه
مثال2 مطلوب است محاسبه
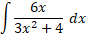
حل: اینانتگرالبه صورت
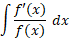
است که در آن+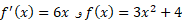 . تابع
. تابع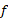 تغییر علامت نمی دهد(همیشه مثبت است). بنابراین معادله(10) را می توان به کار برد، و
تغییر علامت نمی دهد(همیشه مثبت است). بنابراین معادله(10) را می توان به کار برد، و
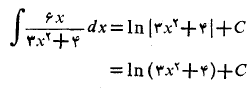
چون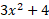 مثبت است، بدون قدرمطلق هم کار انجام می شود.
مثبت است، بدون قدرمطلق هم کار انجام می شود.
 مثال3 مطلوب است محاسبه
مثال3 مطلوب است محاسبه
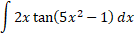
حل: از جانشانی زیر استفاده می کنیم
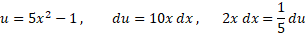
داریم
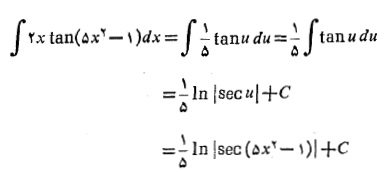
تابع نمایی 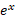
معکوس تابع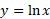 موارد استفاده زیادی درریاضیات و کاربردهایش دارد.
موارد استفاده زیادی درریاضیات و کاربردهایش دارد.
عدد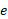
چون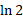 از 1 کمتر و
از 1 کمتر و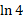 از 1 بیشتر است، طبققضیه مقدار میانگینعددی بین 2و 4 وجود دارد که لگاریتمش برابر 1 است. چون
از 1 بیشتر است، طبققضیه مقدار میانگینعددی بین 2و 4 وجود دارد که لگاریتمش برابر 1 است. چون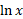 یک به یک است، این عدد یکتاست، و با حرف
یک به یک است، این عدد یکتاست، و با حرف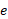 نمایش داده می شد.
نمایش داده می شد.
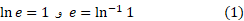
اگر در شکل زیر خط کشی در امتداد خط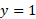 قرار دهید، می بینید که
قرار دهید، می بینید که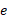 بین 2.5 و 3 واقع می شود.
بین 2.5 و 3 واقع می شود.
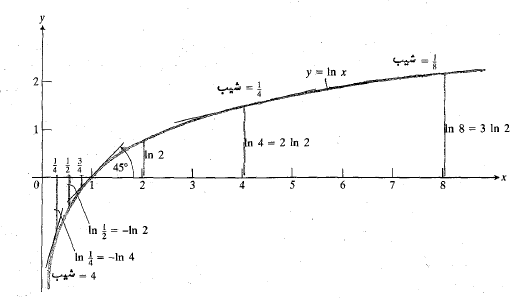
مقدار آن تا 15 عدد اعشار عبارت است از
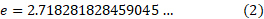
تابع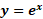
وقتی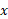 یک عدد گویا باشد، می توانیم
یک عدد گویا باشد، می توانیم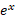 را همان گونه تعریف کنیم که توان های گویای هر عدد مثبت دیگری را تعریف می کنیم. برای این توان های
را همان گونه تعریف کنیم که توان های گویای هر عدد مثبت دیگری را تعریف می کنیم. برای این توان های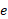 داریم
داریم
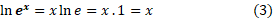
پس وقتی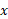 گویا باشد،
گویا باشد،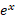 عددی است که لگاریتم طبیعی آن
عددی است که لگاریتم طبیعی آن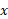 است. با استفاده ازنمادها داریم
است. با استفاده ازنمادها داریم
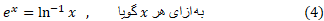
رابطه (4) حاکی است که توابع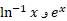 ، وقتی
، وقتی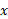 گویا باشد، یکسان اند. این مطلب کلید تعریف
گویا باشد، یکسان اند. این مطلب کلید تعریف 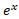 برای سایر مقادیر
برای سایر مقادیر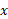 است. هرچند تا اینجا
است. هرچند تا اینجا 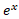 را فقط برای مقادیر گویای
را فقط برای مقادیر گویای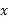 تعریف کرده ایم ولی تابع
تعریف کرده ایم ولی تابع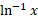 برا ی همه مقادیر
برا ی همه مقادیر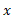 اعم از گویا و گنگ تعریف می شود. بنابراین می توانیم برای تعریف
اعم از گویا و گنگ تعریف می شود. بنابراین می توانیم برای تعریف 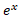 به ازای مقادیری از
به ازای مقادیری از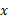 که در مورد آن ها اینجا
که در مورد آن ها اینجا 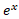 قبلا تعریف نشده است از فرمول اینجا
قبلا تعریف نشده است از فرمول اینجا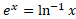 استفاده کنیم. در واقع اگر بخواهیم تابع حاصل پیوسته باشد، هیچ راه دیگری برای تعریف
استفاده کنیم. در واقع اگر بخواهیم تابع حاصل پیوسته باشد، هیچ راه دیگری برای تعریف 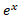 وجود ندارد. پس ناچار به ازای همه
وجود ندارد. پس ناچار به ازای همه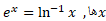 . بنابراین
. بنابراین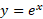 اگر و تنها اگر
اگر و تنها اگر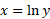 .
.
تعریف تابع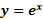 به ازای هر عدد حقیقی
به ازای هر عدد حقیقی
تابع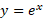 را اغلب تابع نمایی با پایه
را اغلب تابع نمایی با پایه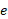 و نمای
و نمای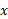 می نامند. نماد دیگری برای
می نامند. نماد دیگری برای 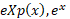 است که «اکسپوتانسیل
است که «اکسپوتانسیل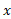 » خوانده می شود. نمودار
» خوانده می شود. نمودار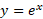 را می توان را با پیدا کردن قرینه
را می توان را با پیدا کردن قرینه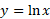 نسبت به خط
نسبت به خط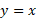 شکل زیر به دست آورد.
شکل زیر به دست آورد.
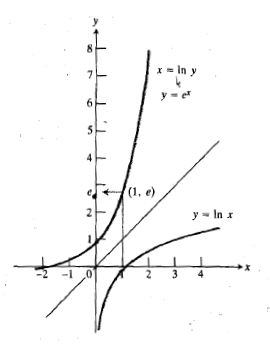
نمودار همان نمودار
همان نمودار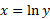 است. این نمودار محور
است. این نمودار محور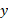 را در
را در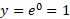 قطع می کند، یعنی
قطع می کند، یعنی

و نیز


معادلات شامل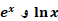
چون 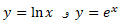 معکوس یکدیگرند،
معکوس یکدیگرند،
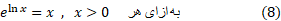
و
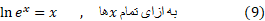
 مثال 1
مثال 1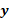 را بیابید.
را بیابید.
الف) 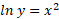
حل :
رابطه را نمایی می کنیم:
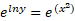
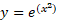
ب)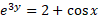
حل: ازدو طرف لگاریتم می گیریم:
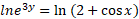
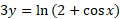
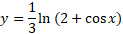
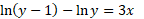
حل:
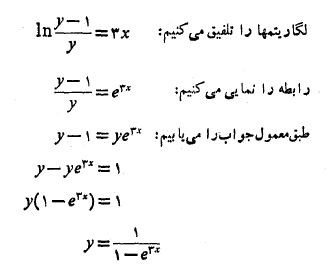
دو قاعده عملی مفید
برای حذف لگاریتم از یک رابطه، دو طرف را نمایی کنید. برای حذف پایه های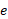 از دو طرف لگاریتم بگیرید.
از دو طرف لگاریتم بگیرید.
قانون نماها
هر چند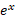 با روشی به ظاهر تصادفی معکوس لگاریتم تعریف شد، ولی از قوانین آشنای نماها در جبر تبعیت می کند
با روشی به ظاهر تصادفی معکوس لگاریتم تعریف شد، ولی از قوانین آشنای نماها در جبر تبعیت می کند


 مثال2ساده کنید
مثال2ساده کنید
الف) 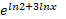
ب) 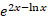
حل:
الف) ( از رابطه 10) 
(تعریف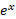 و یکی از ویژگی های لگاریتم)
و یکی از ویژگی های لگاریتم) 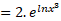

ب) ( از رابطه 10) 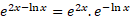
( از رابطه 11) 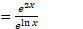
(تعریف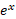 )
) 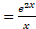
مشتق و انتگرال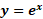
تابع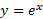 مشتق پذیر است، زیرا معکوس تابع مشتق پذیری است که مشتق آن هرگز صفر نمی شود، برای محاسبهمشتق
مشتق پذیر است، زیرا معکوس تابع مشتق پذیری است که مشتق آن هرگز صفر نمی شود، برای محاسبهمشتق
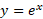
از دو طرف لگاریتم می گیریم
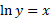
و مشتق ضمنی نسبت به 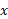 به دست می آوریم
به دست می آوریم
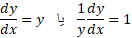
چون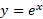 ، از اینجا نتیجه می گیریم که
، از اینجا نتیجه می گیریم که
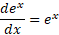
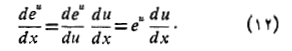
و این به نوبه خود به فرمولانتگرال گیری زیر منجر می شود
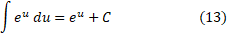
 مثال3
مثال3 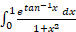
حل: ازجانشانیهای زیر استفاده می کنیم
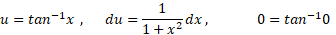
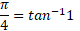
لذا

تابع های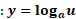 آهنگ های رشد
آهنگ های رشد
با رابطه زیر بحث در مورد آهنگ های رشد تابع های لگاریتمی را آغاز می کنیم.
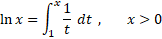
این مطلب به ما امکان داد که با رابطه
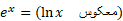
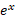 را تعریف کنیم. سپس مطابق قاعده زیر
را تعریف کنیم. سپس مطابق قاعده زیر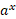 را به ازای هر عدد مثبت
را به ازای هر عدد مثبت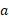 تعریف کردیم
تعریف کردیم
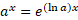
حال در آخرین گام لگاریتم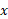 در پایه
در پایه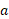 را به صورت زیر تعریف می کنیم
را به صورت زیر تعریف می کنیم
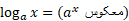
لگاریتم در پایه 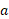
می دانیم که اگر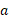 عدد مقبتی بجز 1 باشد، تابع
عدد مقبتی بجز 1 باشد، تابع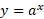 مشتق پذیر و یک به یک است. علاوه براینمشتق آن
مشتق پذیر و یک به یک است. علاوه براینمشتق آن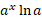 ، هرگزصفر نمی شود. پس این تابع یک معکوس مشتق پذیر دارد، و ما آن را لگاریتم
، هرگزصفر نمی شود. پس این تابع یک معکوس مشتق پذیر دارد، و ما آن را لگاریتم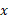 در پایه
در پایه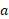 می نامیم و با
می نامیم و با
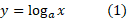
نمایش می دهیم. چون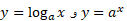 معکوس یکدیگراند، ترکیب آن ها به هر ترتیبی، تابع همانی است. پس روابط زیر به دست می آیند
معکوس یکدیگراند، ترکیب آن ها به هر ترتیبی، تابع همانی است. پس روابط زیر به دست می آیند
(2 الف) به ازای تمام 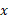 ها ،
ها ، 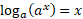
(2 ب) به ازای هر مثبت ،
مثبت ، 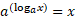
رابطه (2 ب) حاکی است که لگاریتم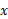 در پایه
در پایه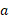 نمایی است که باید
نمایی است که باید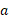 به توان آن برسد تا
به توان آن برسد تا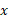 به دست آید. مثلا
به دست آید. مثلا
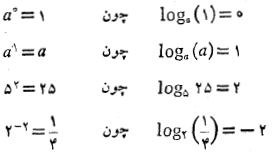
در هر حالت، لگاریتم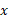 نمایی است که پایه باید به توان آن برسد تا
نمایی است که پایه باید به توان آن برسد تا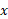 به دست آید. در تساوی
به دست آید. در تساوی
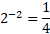
2پایه است و2- لگاریتم 4/1 در پایه 2، نمایی است که 2 باید به توان آن برسد تا 4/1به دست آید. شکل زیر نمودارهای توابع 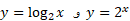 را نشان می دهد.
را نشان می دهد.

محاسبه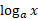
عدد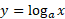 را همیشه می توان به کمک فرمول زیر از لگاریتم های طبیعی
را همیشه می توان به کمک فرمول زیر از لگاریتم های طبیعی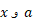 به دست اورد
به دست اورد
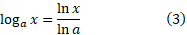
این فرمول را می توان با روش زیر استنتاج کرد. اگر
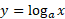
آنگاه
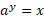
پس
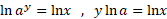
و
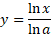
که همان رابطه (3) است.
 مثال1 از رابطه (3) داریم
مثال1 از رابطه (3) داریم
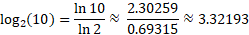
 مثال2
مثال2 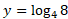 را محاسبه کنید.
را محاسبه کنید.
حل: از رابطه (3) داریم
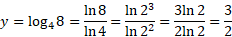
قواعد محاسبه
اگر رابطه (3) را با سه قاعده
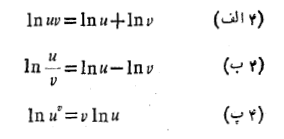
که برای اعداد حقیقی مثبت ( برحسب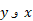 به جای
به جای 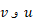 به دست آمد، تلفیق کنیم ، داریم
به دست آمد، تلفیق کنیم ، داریم
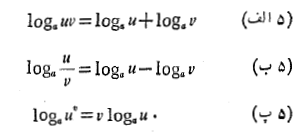
مثلا تساوی (5 پ) با روش زیر به دست می آید
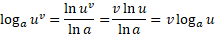
مشتق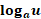
اگر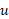 تابع مثبت مشتق پذیری از
تابع مثبت مشتق پذیری از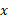 باشد، می توانیم از دو طرف
باشد، می توانیم از دو طرف
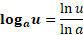
مشتقبگیریم و
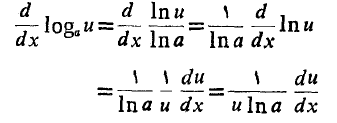
را به دست آوریم. بطورخلاصه
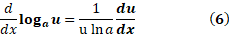
 مثال3مشتق
مثال3مشتق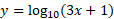 را محاسبه کنید.
را محاسبه کنید.
حل: از رابطه (6) به ازای 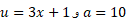 داریم
داریم
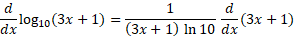
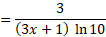
 مثال4 مطلوب است
مثال4 مطلوب است
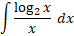
حل: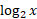 را بر حسب
را بر حسب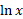 بیان می کنیم
بیان می کنیم
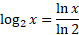
پس
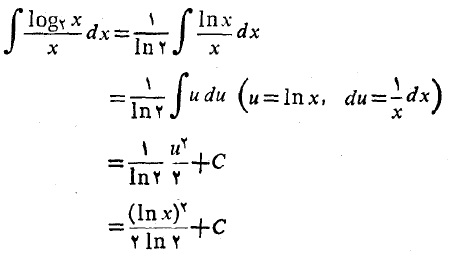
آهنگ های نسبی رشد
ممکن است توجه کرده باشید که توابع نمایی نظیر
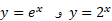
وقتی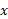 بزرگ می شود، خیلی سریع تر از چند جمله های ها و توابع گویا رشد می کنند. این توابع نمایی مسلما خیلی سریع تر از تابع
بزرگ می شود، خیلی سریع تر از چند جمله های ها و توابع گویا رشد می کنند. این توابع نمایی مسلما خیلی سریع تر از تابع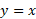 رشد می کنند. تجسم کنید که نمودار تابع
رشد می کنند. تجسم کنید که نمودار تابع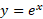 را بر یک تخته سیاه بزرگ رسم می کنید، و واحد مقیاس محورها هم سانتیمتر است. در
را بر یک تخته سیاه بزرگ رسم می کنید، و واحد مقیاس محورها هم سانتیمتر است. در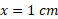 ، ارتفاع نمودار نسبت به محور
، ارتفاع نمودار نسبت به محور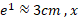 است.
است.
در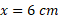 ، ارتفاع نمودار،
، ارتفاع نمودار، 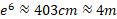 است. در
است. در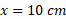 ، ارتفاع نمودار برابر است با
، ارتفاع نمودار برابر است با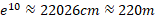 ، یعنی بلندتر از بیشتر ساختمان های موجود است. در
، یعنی بلندتر از بیشتر ساختمان های موجود است. در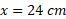 ، نمودار از نیمه راه ماه هم می گذرد، و به ازای
، نمودار از نیمه راه ماه هم می گذرد، و به ازای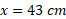 ، نمودار به اندازه ای ارتفاع دارد که از نزدیک ترین ستاره همسایه یعنی از پروکسیماسنچوری هم می گذرد
، نمودار به اندازه ای ارتفاع دارد که از نزدیک ترین ستاره همسایه یعنی از پروکسیماسنچوری هم می گذرد
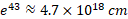
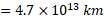
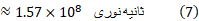
(نور در خلاء با سرعت 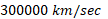 حرکت می کند)
حرکت می کند)
≈5نوریسال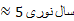
فاصله تا پروکسیماسنچوری در حدود 4.3 سال نوری است. ولی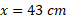 از مبدا بدین معناست که کمتر از نیم متر از محور
از مبدا بدین معناست که کمتر از نیم متر از محور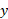 فاصله گرفته ایم.
فاصله گرفته ایم.
در مقابل، توابع لگاریتمی نظیر وقتی
وقتی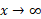 ، از هر توان مثبتی از
، از هر توان مثبتی از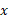 رشد کمتری دارند. اگر محورها را با سانتیمتر مدرج کنیم، باید روی محور
رشد کمتری دارند. اگر محورها را با سانتیمتر مدرج کنیم، باید روی محور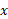 به اندازه 4 سال نوری جلوبرویم تا نقطه ای بیابیم که به ازای آن ارتفاع نمودار
به اندازه 4 سال نوری جلوبرویم تا نقطه ای بیابیم که به ازای آن ارتفاع نمودار 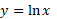 تنها
تنها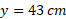 بشود.
بشود.
برای اینکه این مقایسه ها بین توابع نمایی، چند جمله ای و لگاریتمی دقیق باشند باید منظور از «تابعی چون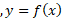 وقتی
وقتی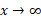 ، تندتر از تابع دیگری چون
، تندتر از تابع دیگری چون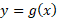 می کند» را تعریف کرد.
می کند» را تعریف کرد.
تعریف آهنگ رشد
وقتی ،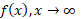 تندتر از
تندتر از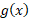 رشد می کند، هرگاه
رشد می کند، هرگاه
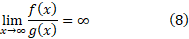
و وقتی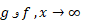 با یک آهنگ رشد می کنند، هرگاه
با یک آهنگ رشد می کنند، هرگاه
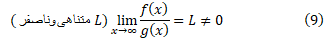
طبق این تعاریف،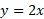 تندتر از
تندتر از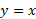 رشد نمی کند. این دو تابع با یک آهنگ رشد می کنند، زیرا
رشد نمی کند. این دو تابع با یک آهنگ رشد می کنند، زیرا
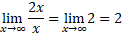
که این حد، متناهی و ناصفر است. دلیل تناقص ظاهری این مطلب با آنچه عقل سلیم حکم می کند این است که ما می خواهیم«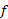 تندتر از
تندتر از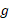 رشد می کند» این معنا را برساند که برای مقادیر بزرگ
رشد می کند» این معنا را برساند که برای مقادیر بزرگ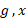 در مقایسه با
در مقایسه با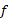 ناچیز باشد.
ناچیز باشد.
 مثال
مثال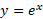 تندتر از
تندتر از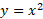 رشد می کند، زیرا
رشد می کند، زیرا
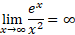
که دوبار استفاده ازقاعده هوپیتال به دست می آید
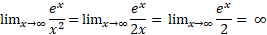
 مثال6 وقتی
مثال6 وقتی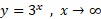 تندتر از
تندتر از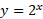 رشد می کند، زیرا
رشد می کند، زیرا
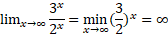
 مثال7 وقتی
مثال7 وقتی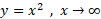 تندتر از
تندتر از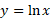 رشد می کند، زیرا
رشد می کند، زیرا
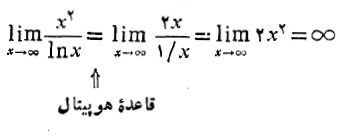
 مثال8 وقتی
مثال8 وقتی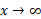 ، آهنگ های رشد
، آهنگ های رشد
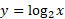
و
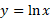
را با هم مقایسه کنید.
حل: نسبت این دو تابع را به هر ترتیب به دست می آوریم و حد این نسبت را وقتی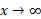 محاسبه می کنیم
محاسبه می کنیم
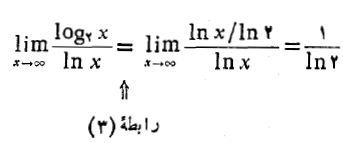
این حد، متناهی و ناصفر است. لذا دیده می شود که لگاریتم ها، هر چند پایه های متفاوتی داشته باشند، با یک آهنگ رشد می کنند.
همانگونه که از مثال(8) بر می آید، هر دو تابع لگاریتمی 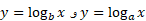 ، وقتی
، وقتی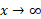 ، با یک آهنگ رشد می کنند. برای مشاهده دلیل این امر حد زیر را محاسبه می کنیم
، با یک آهنگ رشد می کنند. برای مشاهده دلیل این امر حد زیر را محاسبه می کنیم
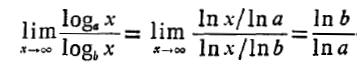
این حد همیشه متناهی و مخالف با صفر است. علی رغم رفتار توابع لگاریتمی، دو تابع مختلف نمایی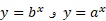 وقتی
وقتی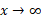 ، با آهنگ های متفاوتی رشد می کنند. این مطلب از محاسبه
، با آهنگ های متفاوتی رشد می کنند. این مطلب از محاسبه
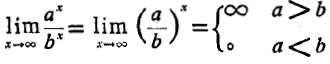
دیده می شود. اگر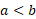 ، آنگاه
، آنگاه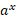 تندتر از
تندتر از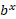 رشد می کند. اگروقتی
رشد می کند. اگروقتی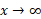 ، آهنگ رشد
، آهنگ رشد 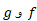 یکسان و آهنگ رشد
یکسان و آهنگ رشد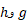 هم یکسان باشد، آنگاه
هم یکسان باشد، آنگاه 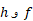 با یک آهنگ رشد می کنند.دلیلش این است که از
با یک آهنگ رشد می کنند.دلیلش این است که از
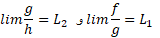
نتیجه می گیریم
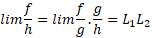
 مثال9 نشان دهید که وقتی
مثال9 نشان دهید که وقتی 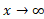 ،
،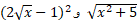 با یک آهنگ رشد می کنند.
با یک آهنگ رشد می کنند.
حل: برای اینکه نشان دهیمآهنگ رشد این دو تابع یکسان است، نشان می دهیم آهنگ رشد هر دو با آهنگ رشد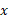 یکی است.
یکی است.
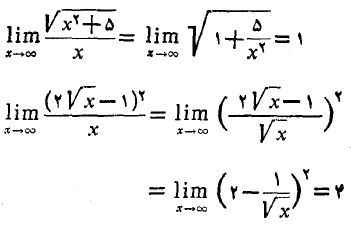
برای مطالعه مباحث بیشتر از محصول کپسول آموزش ریاضی عمومی 1 استفاده کنید.