طول خم های واقع در صفحه
طول یک مسیر خمیده در یک صفحه را به همان طریقی تقریب می زنیم که طول یک جاده خمیده را روی نقشه به کمک خط کش برآورد می کنیم: طول پاره خط هایی را که دو سر آن ها روی خم است جمع می کنیم. این برآورد همواره حدی از دقت دارد که به دقت اندازه گیری و تعداد پاره خط ها بستگی دارد.
به کمک حساب دیفرانسیل و انتگرال می توان این کار را بهتر انجام داد زیرا می توانیم پاره خط ها را هرچه بخواهیم کوچک بگیریم، به طوری که خط شکسته ای که از پاره خط ها پدید می آید، هرچه بیشتر برخم منطبق باشد. با انجام دادن این کار می توان آن را با یک انتگرال محاسبه کرد.

فرمول اصلی دکارت
فرض می کنیم نمودار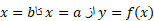 خمی باشد که محاسبه طولش مطلوب ما است (شکل زیر).
خمی باشد که محاسبه طولش مطلوب ما است (شکل زیر).
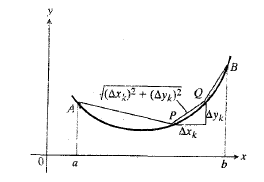
این خم را به 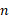 قطعه تقسیم و نقاط تقسیم پیاپی را به هم وصل می کنیم تا تعدادی پاره خط به دست آید. طول یک پاره خط نمونه چون
قطعه تقسیم و نقاط تقسیم پیاپی را به هم وصل می کنیم تا تعدادی پاره خط به دست آید. طول یک پاره خط نمونه چون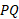 چنین است
چنین است
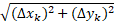
طول خم از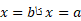 را با مجموع زیر تقریب می زنیم
را با مجموع زیر تقریب می زنیم

انتظار می رود که وقتی تعداد پاره خط ها بهبینهایتو طول هر یک از آن ها به صفر میل کند، تقریب بهتر شود. همچنین می خواهیم نشان دهیم که مجموع فوق به حدی محاسبه پذیر میل می کند. برای اثبات این موضوع آن را به صورتی می نویسیم که بتوان قضیه وجود انتگرال را به کار برد.
فرض می کنیم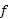 مشتقی دارد که در هر نقطه از
مشتقی دارد که در هر نقطه از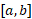 پیوسته است. در این صورت، بنا بهقضیه مقدار میانگیننقطه ای مانند
پیوسته است. در این صورت، بنا بهقضیه مقدار میانگیننقطه ای مانند 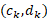 روی خم و بین
روی خم و بین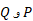 وجود دارد که در آن مماس بر خط موازی وتر
وجود دارد که در آن مماس بر خط موازی وتر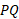 است. یعنی
است. یعنی
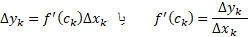
مجموع موجود در عبارت(1) با اینجانشانی به صورت زیر در می آید
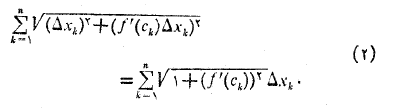
اکنون مشاهده می شود که این مجموع، انتگرال زیر را تقریب می زند
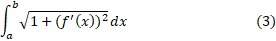
بنابراین حد مجموع وقتی که تقسیمات ظریف تر و ظریف تر می شوند برابر با این انتگرال است. پس طول خم را از 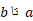 تعریف می کنیم. معمولا
تعریف می کنیم. معمولا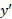 را جای
را جای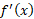 قرار می دهند و فرمول انتگرال را ساده می کنند.
قرار می دهند و فرمول انتگرال را ساده می کنند.
تعریف
طول خم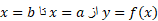

 مثال1 طول خم زیر را از
مثال1 طول خم زیر را از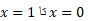 بیابید.
بیابید.
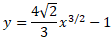
حل: طول را از معادله (4) محاسبه می کنیم
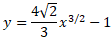
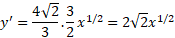
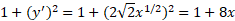
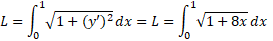
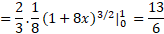
فرمول پارامتری
برای محاسبه طول خمی که با معادلات پارامتری مشخص می شود فرمول بسیار مفیدی وجود دارد. فرض کنید معادلات عبارت اند از
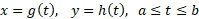
و نقطه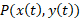 وقتی که
وقتی که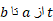 می رود دقیقا یک بار خم را طی می کند. برای تقسیم بندی خم، به جای تقسیم بندی محور
می رود دقیقا یک بار خم را طی می کند. برای تقسیم بندی خم، به جای تقسیم بندی محور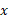 ، بازه
، بازه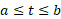 را تقسیم بندی می کنیم. به این ترتیب خم مانند شکل زیر تقسیم بندی می شود.
را تقسیم بندی می کنیم. به این ترتیب خم مانند شکل زیر تقسیم بندی می شود.
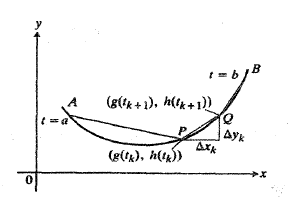
چنانکه در شکل دیده می شودمختصات دو نقطه پیاپی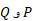 عبارت اند از
عبارت اند از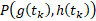 و
و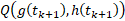 . بنابراین طول پاره خط
. بنابراین طول پاره خط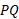 را می توان به کمک قضیه فیثاغورس چنین محاسبه کرد.
را می توان به کمک قضیه فیثاغورس چنین محاسبه کرد.
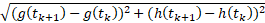
(این فرمول را بزودی ساده می کنیم)
اگر مشتقات اول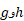 موجود و در
موجود و در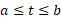 پیوسته باشند، بنا بهقضیه مقدار میانگین داریم
پیوسته باشند، بنا بهقضیه مقدار میانگین داریم
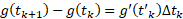
(5)
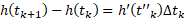
که در آن ها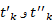 مقادیر مناسبی اند که بین
مقادیر مناسبی اند که بین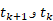 انتخاب می شوند. بنابراین مجموع طول های پاره خط های تقریب زننده خم به صورت زیر در می آید
انتخاب می شوند. بنابراین مجموع طول های پاره خط های تقریب زننده خم به صورت زیر در می آید
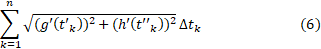
این مجموع، مجموع ریمان تابعی نیست زیرا ضرورت ندارد نقاط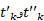 یکی باشند. اما قضیه ای به نام قضیه بلیس (که در کتاب های پیشرفته تر اثبات می شود) ما را مطمئن می سازد که مجموع ها همگرایند و مقدار آن ها برابر انتگرال زیر است
یکی باشند. اما قضیه ای به نام قضیه بلیس (که در کتاب های پیشرفته تر اثبات می شود) ما را مطمئن می سازد که مجموع ها همگرایند و مقدار آن ها برابر انتگرال زیر است
طول خم پارامتری 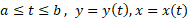
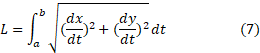
 مثال2 مکان ذره
مثال2 مکان ذره 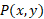 در زمان
در زمان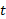 عبارت است از .
عبارت است از .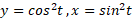 این ذره بین
این ذره بین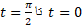 چه مسافتی را می پیماید.
چه مسافتی را می پیماید.
حل: مسافتی را که ذره از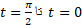 می پیماید از رابطه (7) به دست می آوریم
می پیماید از رابطه (7) به دست می آوریم
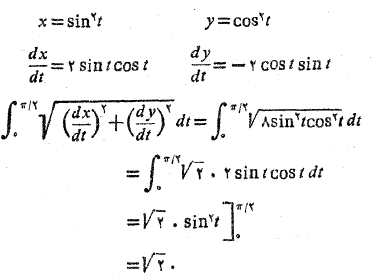
در این حالت درستی نتایج را می توان از راه هندسی بررسی کرد. چون به ازای همه مقادیر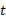 داریم
داریم
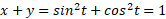
مطابق شکل زیر مسیر ذره پاره خط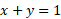 است که از(0,1) که در آن
است که از(0,1) که در آن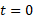 تا(0,1) که در آن
تا(0,1) که در آن 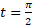 امتداد دارد.
امتداد دارد.
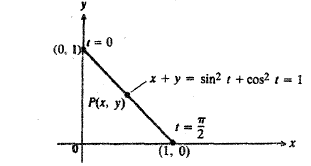
طول این پاره خط چنین است
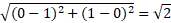

فرمول دیفرانسیلی ساده
معمولا رابطه 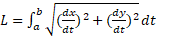 را به جای مشتقات با دیفرانسیل ها نمایش می دهند. از لحاظ صوری این عمل چنین انجام می شود که مشتقات را به صورت خارج قسمت های دیفرانسیل ها در نظر می گیرند و
را به جای مشتقات با دیفرانسیل ها نمایش می دهند. از لحاظ صوری این عمل چنین انجام می شود که مشتقات را به صورت خارج قسمت های دیفرانسیل ها در نظر می گیرند و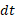 را به صورت
را به صورت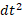 به زیر رادیکال می آورند و به این ترتیب دیفرانسیل های مخرج را حذف می کنند
به زیر رادیکال می آورند و به این ترتیب دیفرانسیل های مخرج را حذف می کنند
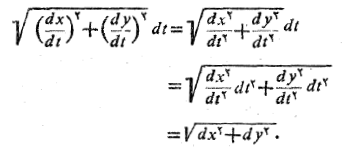
در نتیجه فرمول طول خم به صورت زیر در می آید

البته قبل از انجام انتگرال گیری در رابطه(8) باید 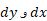 را برحسب یکی از متغیرها بیان و حدود مناسبی برای انتگرال گیری تعیین کرد. رابطه (8) را باز هم می توان کوتاهتر کرد.
را برحسب یکی از متغیرها بیان و حدود مناسبی برای انتگرال گیری تعیین کرد. رابطه (8) را باز هم می توان کوتاهتر کرد.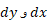 را می توان دو ضلع مثلث کوچکی در نظر گرفت که وتر آن
را می توان دو ضلع مثلث کوچکی در نظر گرفت که وتر آن
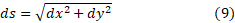
دیفرانسیل طول قوسی است که می توان از ان بین حدود مناسبی انتگرالگرفت وطول خم را به دست آورد مانند شکل.
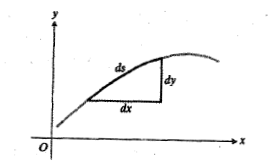
ترتیب رابطه(8) چنین می شود
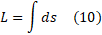
 مثال3 نشان دهید که به کمک فرمول
مثال3 نشان دهید که به کمک فرمول 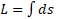 می توان محیط یک دایره به شعاعr
می توان محیط یک دایره به شعاعr را تعیین کرد.
را تعیین کرد.
حل: معادلات پارامتری دایره را می نویسیم
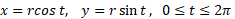
همانند شکل
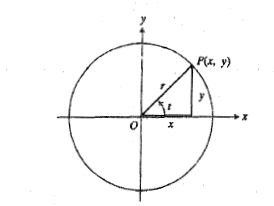
بنابراین
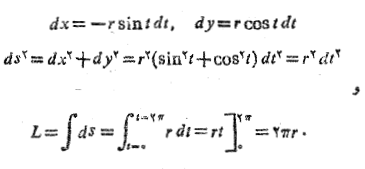
ناپیوستگی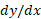
در نقطه ای از یک خم که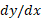 وجود ندارد، ممکن است
وجود ندارد، ممکن است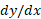 موجود باشد و شاید بتوان با یک یا چند بار استفاده از فرمول زیر که همان رابطه (4) با تعویض
موجود باشد و شاید بتوان با یک یا چند بار استفاده از فرمول زیر که همان رابطه (4) با تعویض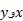 است طول خم را یافت
است طول خم را یافت
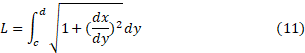
 مثال4 طول خم
مثال4 طول خم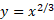 را بین
را بین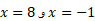 را بیابید.
را بیابید.
حل: خم را رسم می کنیم مانند شکل و مشتقش را می آزماییم
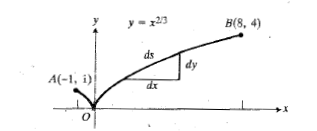
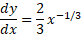
چون مشتق در مبدا بینهایت می شود، طول خم را، به جای رابطه (4)، از رابطه (11) به دست می آوریم. معادله 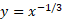 را نسبت به
را نسبت به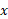 حل می کنیم و چنین نتیجه می گیریم
حل می کنیم و چنین نتیجه می گیریم
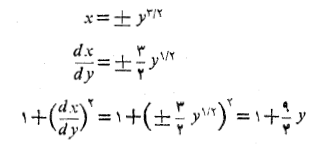
طول قسمتی از خم که بین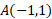 و مبدا قرار دارد برابر است با
و مبدا قرار دارد برابر است با
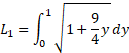
طول قسمتی از خم که بین مبدا و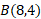 قرار دارد چنین است
قرار دارد چنین است
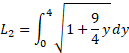
طول کل خم عبارت است از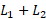 .
.
برای محاسبهL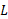 باید از دو انتگرال جداگانه استفاده کنیم زیرا معادله
باید از دو انتگرال جداگانه استفاده کنیم زیرا معادله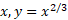 را به صورت دو تابع جداگانه از
را به صورت دو تابع جداگانه از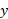 تعریف می کند. قوس
تعریف می کند. قوس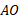 را فرمول
را فرمول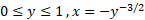 و قوس
و قوس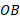 را فرمول
را فرمول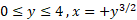 مشخص می کند.
مشخص می کند.
برای محاسبه انتگرال های ، جانشانی های
، جانشانی های
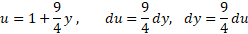
را به کار می بریم و چنین به دست می آوریم
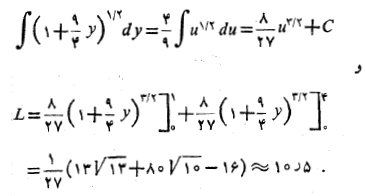
برای اطمینان از اینکه در محاسبات خطا پیش نیانده است، می توان مجموع طول وترهای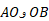 را محاسبه و درستی نتایج را بررسی کرد.
را محاسبه و درستی نتایج را بررسی کرد.
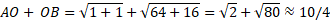
بنابراین به نظر می رسد جواب های به دست آمده معقول است.
مبدا در شکل فوق یک نقطه بازگشت است. در این نقطه شیب بینهایت می شود. چنانچه می خواستیم برای این خم خاص رابطه (4) را بدست آوریم، در می یافتیم که برای هر وتری چون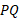 که بر نقطه بازگشت پلمی زند نمی توانیم مرحله ای را که نیاز به قضیه مقدار میانگین دارد طی کنیم.
که بر نقطه بازگشت پلمی زند نمی توانیم مرحله ای را که نیاز به قضیه مقدار میانگین دارد طی کنیم.
اما قضیه مقدار میانگین را می توان در مورد وتری که به نقطه بازگشت منتهی می شود یا از آن آغاز می شود به کاربرد، زیرا در این قضیهمشتق پذیر بودن در نقاط انتهایی ضرورت ندارد. بنابراین فرمولی که به جای رابطه (4) به دست خواهد آمد شامل دو انتگرال است: یکی طول از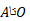 و دیگری طول از
و دیگری طول از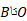 را به دست می دهد.
را به دست می دهد.
قاعده معمول در این مورد چنین است: هرگاه خمی یک یا چند نقطه بازگشت داشته باشد، طول آن را باانتگرال گیری از خم بین هر دو نقطه بازگشت و جمع نتایج به دست می آوریم.

مساحت رویه های دورانی
هنگامی که طناب بازی می کنید، طناب رویه ای را می روید. چنین به نظر می رسد که مساحت رویه به طول طناب و شعاع دوران هر قطعه از آن بستگی داشته باشد. در ادامه ارتباط میان مساحت یک رویه دورانی با طول و شعاع خمی که آن را ایجاد می کند بررسی می شود.
تعریف مساحت رویه و فرمول دکارت
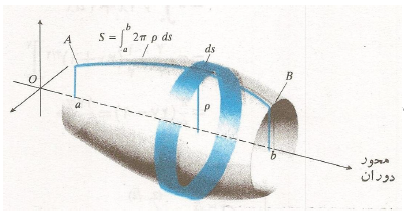
فرض کنید خمی چون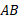 مطابق شکل زیر قسمت (الف ) حول محور
مطابق شکل زیر قسمت (الف ) حول محور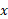 دوران می کند و رویه ای پدید می آورد. اگر
دوران می کند و رویه ای پدید می آورد. اگر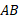 را با یک خط شکسته محاط در خم نظیر خط شکسته ای که برای تعریف طول قوس به کاربردیم تقریب بزنیم، هر قطعه
را با یک خط شکسته محاط در خم نظیر خط شکسته ای که برای تعریف طول قوس به کاربردیم تقریب بزنیم، هر قطعه 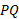 از خط شکسته مخروط ناقصی به وجود می آورد که محورش بر محور
از خط شکسته مخروط ناقصی به وجود می آورد که محورش بر محور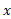 منطبق است. تصویر بزرگ شده مخروط ناقص در قسمت (ب)شکل زیر دیده می شود.
منطبق است. تصویر بزرگ شده مخروط ناقص در قسمت (ب)شکل زیر دیده می شود.
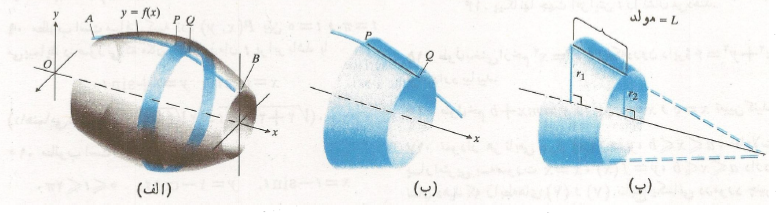
مطابق قسمت (پ) شکل شعاع قاعده های مخروط ناقص را با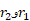 مولد آن را با
مولد آن را با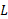 نشان می دهیم. بنابراین
نشان می دهیم. بنابراین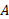 ، مساحت جانبی این مخروط ناقص، برابر است با
، مساحت جانبی این مخروط ناقص، برابر است با

مجموع مساحات جانبی این مخروط های ناقص که ازدوران قطعات خط شکسته محاطی از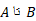 به وجود می آیند تقریبی است از
به وجود می آیند تقریبی است از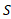 ، مساحت رویه ای که از دوران خم
، مساحت رویه ای که از دوران خم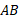 ایجاد می شود. این تقریب به طریق زیر به یک فرمول انتگرالی برای از
ایجاد می شود. این تقریب به طریق زیر به یک فرمول انتگرالی برای از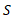 منجر می شود.
منجر می شود.
فرض می کنیم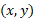 مختصات
مختصات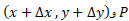 مختصات
مختصات 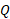 باشد. به این ترتیب ابعاد مخروط ناقص حاصل از دوران پاره خط
باشد. به این ترتیب ابعاد مخروط ناقص حاصل از دوران پاره خط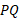 چنین است
چنین است
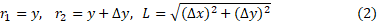
بنا به رابطه(1)، مساحت جانبی مخروط ناقص چنین است
 مساحت جانبی مخروط ناقص
مساحت جانبی مخروط ناقص
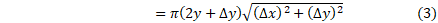
با جمع کردن مساحات مخروط های ناقص روی بازه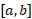 از چپ به راست داریم
از چپ به راست داریم
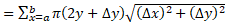 مجموع مساحات مخروط های ناقص
مجموع مساحات مخروط های ناقص
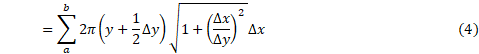
اگر 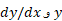 توابع پیوسته ای از
توابع پیوسته ای از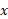 باشند، می توان نشان داد که حد این مجموع چنین است
باشند، می توان نشان داد که حد این مجموع چنین است
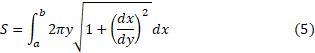
برای به دست آوردن این حد از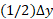 در رابطه (4) چشم پوشیدیم. به این ترتیب مساحت رویه را برابر با مقدار انتگرال زیر تعریف می کنیم.
در رابطه (4) چشم پوشیدیم. به این ترتیب مساحت رویه را برابر با مقدار انتگرال زیر تعریف می کنیم.
تعریف مساحت رویه
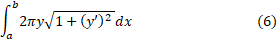
 مثال 1 مطلوب است مساحت رویه حاصل از دوران خم
مثال 1 مطلوب است مساحت رویه حاصل از دوران خم
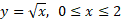
حول محور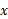 بیابید مطابق شکل زیر.
بیابید مطابق شکل زیر.
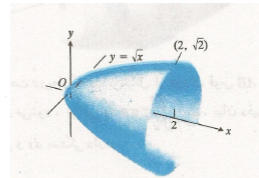
حل: برای به دست آوردن مساحت رویه، رابطه (6) را به ازای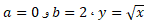 به کار می بریم
به کار می بریم
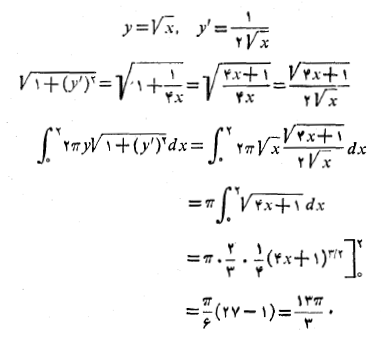
صورت های دیگر انتگرال
اگر محور دوران محور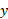 باشد، به جای فرمول(6) از فرمول زیر استفاده می کنیم
باشد، به جای فرمول(6) از فرمول زیر استفاده می کنیم
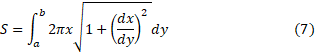
اگر معادلات خمی که رویه را ایجاد می کنند به صورت پارامتری باشند، مثلا به این ترتیب که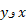 توابعی از متغیرسومی چون t باشند که از
توابعی از متغیرسومی چون t باشند که از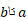 تغییر می کند، آنگاه برای محاسبه
تغییر می کند، آنگاه برای محاسبه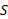 می توان از فرمول زیر بهره گرفت
می توان از فرمول زیر بهره گرفت
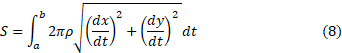
در این فرمول،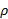 فاصله محور دوران از جزء طول قوس است و به صورت تابعی از
فاصله محور دوران از جزء طول قوس است و به صورت تابعی از 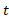 بیان می شود. همه فرمول های مربوط به مساحت رویه ها به صورت زیرا ند
بیان می شود. همه فرمول های مربوط به مساحت رویه ها به صورت زیرا ند
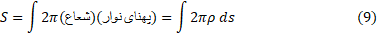
که در آن،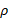 شعاع دوران جزء طول قوس
شعاع دوران جزء طول قوس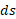 شکل زیر است. اگر بخواهید تنها یک فرمول در مورد مساحت رویه به خاطر بسپارید، این فرمول مناسب است. در این صورت، درهر مساله خاص باید تابع شعاع،
شکل زیر است. اگر بخواهید تنها یک فرمول در مورد مساحت رویه به خاطر بسپارید، این فرمول مناسب است. در این صورت، درهر مساله خاص باید تابع شعاع،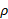 ، و دیفرانسیل طول قوس،
، و دیفرانسیل طول قوس،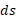 ، را بر حسب یک متغیر بیان کرده و حدودانتگرال گیریرا مشخص کنید.
، را بر حسب یک متغیر بیان کرده و حدودانتگرال گیریرا مشخص کنید.
 مثال2 دایره
مثال2 دایره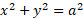 را حول خط
را حول خط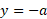 که در نقطه
که در نقطه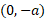 بر دایره مماس است دوران می دهیم. مطلوب است مساحت رویه ایجاد شده. مطابق شکل
بر دایره مماس است دوران می دهیم. مطلوب است مساحت رویه ایجاد شده. مطابق شکل

حل: در اینجا باید کل دایره را در نظر گرفت. یعنی باید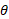 را از
را از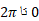 تغییر داد. شعاع دوران چنین است
تغییر داد. شعاع دوران چنین است
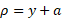
و داریم
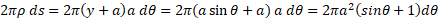
از این رو بنا به رابطه (9) داریم
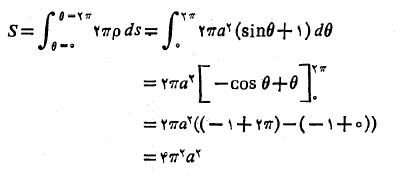
مثال3 مطلوب است مساحت کره ای که از دوران دایره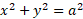 حول محورx به وجود می آید. شکل زیر
حول محورx به وجود می آید. شکل زیر
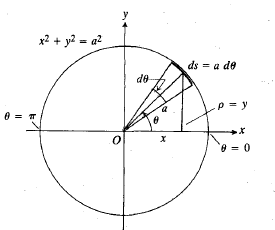
حل: نیمه بالایی این دایره کل کره را ایجاد می کند. معادلات این نیمدایره این ها هستند
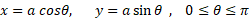
بنابراین
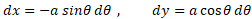
و
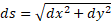
و
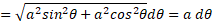
اکنون از رابطه (9) چنین به دست می آید
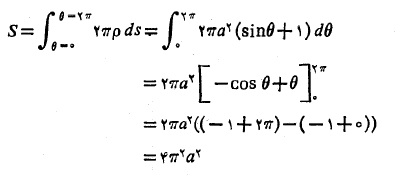
برای مطالعه و یادگیری مباحث بیشتر در این زمینه از محصولکپسول آموزش ریاضی عمومی 1 استفاد کنید.