حد و بینهایت و پیوستگی
کاربرد حد:
می دانیم که برای به دست آوردنمشتق، لازم است حد را محاسبه کنیم. در هنگام محاسبه حد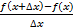 وقتی
وقتی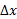 به صفر میل می کند،
به صفر میل می کند،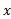 را ثابت مگه می داریم در حالی که
را ثابت مگه می داریم در حالی که 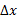 تغییر می کند. در این حالت کل خارج قسمت را به عنوان تابعی از یک متغیر
تغییر می کند. در این حالت کل خارج قسمت را به عنوان تابعی از یک متغیر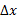 درنظر می گیریم.
درنظر می گیریم.

فرض کنید مقادیر تابعی چون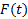 را در حالی که
را در حالی که 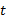 به سمتc حرکت می کند بدون آنکه عملا مقدارcرا اختیار کند(همانطور که
به سمتc حرکت می کند بدون آنکه عملا مقدارcرا اختیار کند(همانطور که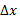 به 0 میل می کند بدون آنکه مقدار 0 تغییر کند). وقتی
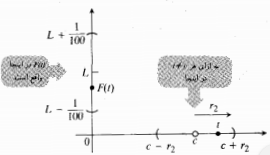
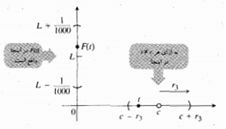
به 0 میل می کند بدون آنکه مقدار 0 تغییر کند). وقتی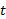 در محدوده ای به مرکزc و به شعاعr1 قرار دارد،
در محدوده ای به مرکزc و به شعاعr1 قرار دارد،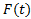 در محدوده ای به مرکزL و به شعاع یک دهم واحد واقع است.
در محدوده ای به مرکزL و به شعاع یک دهم واحد واقع است.
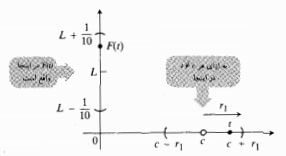
وقتی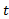 حرکت خود را به سمتc ادامه می دهد،
حرکت خود را به سمتc ادامه می دهد،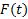 باید نهایتا بهL نزدیک و نزدیکتر شود. مثلا به ازای همه مقادیر
باید نهایتا بهL نزدیک و نزدیکتر شود. مثلا به ازای همه مقادیر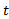 در محدوده ای به مرکزcو به شعاع کوچکترr2،
در محدوده ای به مرکزcو به شعاع کوچکترr2،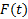 در محدوده ای به مرکزLو به شعاع
در محدوده ای به مرکزLو به شعاع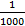 واحد قرار داشته باشد.
واحد قرار داشته باشد.
لازم است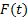 پس از مدتی در داخل محدوده ای به مرکزLو به شعاع
پس از مدتی در داخل محدوده ای به مرکزLو به شعاع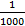 واحد قرار گیرد. یعنی به ازای همه مقادیر
واحد قرار گیرد. یعنی به ازای همه مقادیر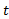 در محدوده ای به مرکزcوبه شعاعr3، که ازr2 هم کوچکتر است، تمام مقادیر
در محدوده ای به مرکزcوبه شعاعr3، که ازr2 هم کوچکتر است، تمام مقادیر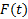 در بازه
در بازه
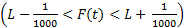 واقع باشند.
واقع باشند.
درواقع لازم است که به ازای هر بازه ی حول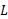 ، هر قدر کوچک، بتوانیم بازه ای از اعداد حول C بیابیم که همه مقادیر
، هر قدر کوچک، بتوانیم بازه ای از اعداد حول C بیابیم که همه مقادیر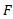 آن ها در داخل آن بازه ی حول
آن ها در داخل آن بازه ی حول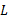 باشند. به ازای هر شعاع مثبت
باشند. به ازای هر شعاع مثبت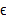 حول
حول 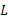 ، یک شعاع مثبت
، یک شعاع مثبت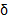 حول Cوجود داشته باشد به قسمی که برای همه مقادیر
حول Cوجود داشته باشد به قسمی که برای همه مقادیر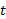 در محدوده ای به مرکز Cو به شعاع
در محدوده ای به مرکز Cو به شعاع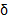 واحد (به استثنای
واحد (به استثنای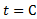 ) مقادیر
) مقادیر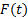 در محدوده ای به مرکز
در محدوده ای به مرکز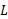 و به شعاع
و به شعاع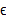 واحد واقع باشند. بنابراین هر قدر
واحد واقع باشند. بنابراین هر قدر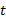 بدون مساوی شدن با
بدون مساوی شدن با به
به 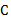 نزدیکتر شود،
نزدیکتر شود،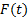 نیز باید به
نیز باید به 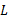 نزدیکتر شود.
نزدیکتر شود.
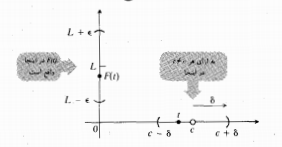
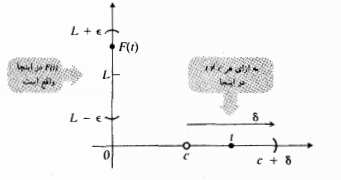
تعریف حد
حد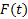 وقتی
وقتی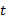 به سمت C میل می کند، عدد
به سمت C میل می کند، عدد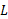 است اگر: به ازای هر شعاع
است اگر: به ازای هر شعاع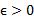 حول
حول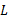 ، یک شعاع
، یک شعاع 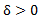 حول C وجود داشته باشد به قسمی که به ازای هر
حول C وجود داشته باشد به قسمی که به ازای هر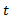 داریم :
داریم :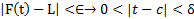
عبارت «حد 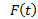 وقتی
وقتی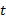 به C میل می کند، برابر
به C میل می کند، برابر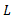 است» را می توان به صورت
است» را می توان به صورت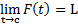 نوشت.
نوشت.
وقتی می گوییم 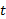 به سمت C میل می کند
به سمت C میل می کند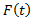 به حد
به حد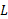 می گراید، یعنی اینکه به ازای هر
می گراید، یعنی اینکه به ازای هر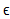 مثبت یک عدد کوچک
مثبت یک عدد کوچک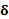 مثبت وجود دارد (که به
مثبت وجود دارد (که به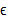 وابسته است) بطوری که اگر
وابسته است) بطوری که اگر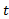 مقید به محدوده ای به مرکز C و شعاع
مقید به محدوده ای به مرکز C و شعاع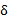 واحد باشد،
واحد باشد،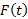 در محدوده ای به مرکز
در محدوده ای به مرکز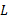 و به شعاع
و به شعاع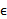 واحد قرار دارد.
واحد قرار دارد.
حد چپ و حد راست
حد تابع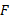 را وقتی
را وقتی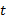 از سمت راست به C میل می کند حد راست
از سمت راست به C میل می کند حد راست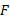 در C ، و حد تابع
در C ، و حد تابع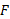 را وقتی
را وقتی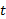 از سمت چپ به C میل می کند حد چپ
از سمت چپ به C میل می کند حد چپ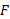 در C می نامیم.
در C می نامیم.

تعریف حد راست: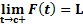
حد تابع 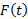 وقتی
وقتی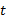 از سمت راست به C میل می کند برابر با
از سمت راست به C میل می کند برابر با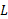 است اگر: به ازای هر
است اگر: به ازای هر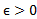 مفروض (هر شعاع حول
مفروض (هر شعاع حول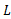 ) یک
) یک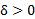 (شعاعی در سمت راست C) وجود داشته باشد که به ازای هر
(شعاعی در سمت راست C) وجود داشته باشد که به ازای هر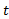 ،
،
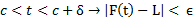
تعریف حد چپ: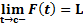
حد تابع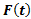 وقتی
وقتی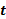 از چپ به C میل می کند کند برابر با
از چپ به C میل می کند کند برابر با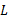 است اگر: به ازای هر
است اگر: به ازای هر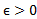 مفروض (هر شعاع حول
مفروض (هر شعاع حول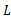 ) یک
) یک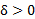 (شعاعی در سمت چپ C) وجود داشته باشد که به ازای هر
(شعاعی در سمت چپ C) وجود داشته باشد که به ازای هر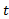 ،
،
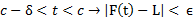
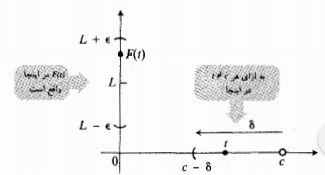
از مقایسه روابط
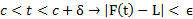
و
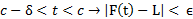
با
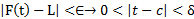
ارتباط حدهای چپ و راست در یک نقطه با حدی که قبلا تعریف شد معلوممی شود. اگر را از عناصر نامساوی های
را از عناصر نامساوی های 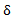 در روابط
در روابط 1 و2 کم کنیم این نامساوی ها به شکل زیر در می آیند.
1 و2 کم کنیم این نامساوی ها به شکل زیر در می آیند.
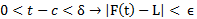 (
(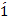 )
)
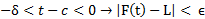 (
(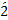 )
)
روابط (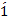 ) و (
) و (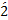 ) بر روی هم معادل رابطه زیر را تشکیل می دهند.
) بر روی هم معادل رابطه زیر را تشکیل می دهند.
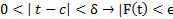
بطور خلاصه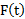 در یک نقطه دارای حد است اگر و تنها اگر حدهای راست و چپ در آنجا موجود و برابر با هم باشند. گاهی
در یک نقطه دارای حد است اگر و تنها اگر حدهای راست و چپ در آنجا موجود و برابر با هم باشند. گاهی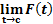 را در حد دو طرفه
را در حد دو طرفه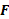 در
در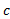 می نا میم تا آن را از حدهای یک طرفه راست وچپ
می نا میم تا آن را از حدهای یک طرفه راست وچپ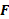 در
در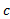 متمایز کنیم.
متمایز کنیم.
رابطه بین حدهای یک طرفه و دوطرفه
تابعی چون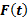 در نقطه ای مانند
در نقطه ای مانند دارای حد است اگر و تنها اگر حدهای راست و چپ در
دارای حد است اگر و تنها اگر حدهای راست و چپ در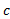 موجود و برابر با هم باشند.
موجود و برابر با هم باشند.
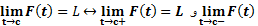
حد و بینهایت
حد وقتی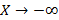 یا
یا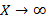 تابع
تابع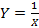 به ازای همه اعداد حقیقی بجز
به ازای همه اعداد حقیقی بجز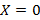 تعریف می شود. درمورد گزاره های زیر به وضوح صدق می کنند.
تعریف می شود. درمورد گزاره های زیر به وضوح صدق می کنند.
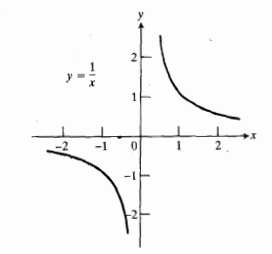
الف- وقتی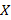 کوچک و مثبت است،
کوچک و مثبت است،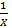 بزرگ ومثبت است. مثلا
بزرگ ومثبت است. مثلا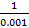
ب- وقتی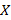 کوچک و منفی است،
کوچک و منفی است،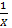 بزرگ ومنفی است. مثلا
بزرگ ومنفی است. مثلا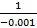
پ- وقتی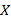 بزرگ و مثبت است،
بزرگ و مثبت است،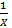 کوچک ومثبت است. مثلا
کوچک ومثبت است. مثلا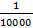
ت- وقتی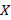 بزرگ و منفی است،
بزرگ و منفی است،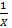 کوچک ومنفی است. مثلا
کوچک ومنفی است. مثلا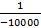
خلاصه چهار گزاره بالا به این ترتیب است:
الف- وقتیX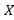 از سمت راست به 0 میل می کند،
از سمت راست به 0 میل می کند،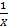 به
به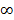 می گراید.
می گراید.
ب- وقتی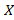 از سمت چپ به 0 میل می کند،
از سمت چپ به 0 میل می کند،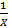 به
به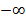 می گراید.
می گراید.
پ- وقتی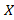 به
به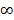 می گراید،
می گراید،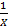 به
به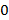 میل می کند.
میل می کند.
ت- وقتی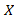 به
به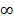 - می گراید،
- می گراید،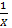 به
به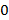 میل می کند.
میل می کند.
علامت بینهایت نشان دهنده هیچ عدد حقیقی نیست. نمی توانیم 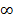 را درحساب به روش معمول به کار ببریم، ولی بهتر است بتوانیم جمله هایی از قبیل « حد
را درحساب به روش معمول به کار ببریم، ولی بهتر است بتوانیم جمله هایی از قبیل « حد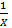 وقتی به
وقتی به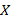 به بینهایت میل می کند صفر است» را بر زبان آوریم.
به بینهایت میل می کند صفر است» را بر زبان آوریم.
تعریف حد وقتی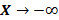 یا
یا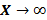
1.حد تابع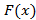 وقتی
وقتی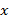 به بینهایت میل می کند عددL است،
به بینهایت میل می کند عددL است،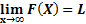 اگر به ازای هر
اگر به ازای هر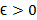 یک عددM وجود داشته باشد بطوری که به ازای هر
یک عددM وجود داشته باشد بطوری که به ازای هر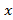 ،
،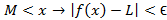 برقرار باشد.
برقرار باشد.
2.حدF(x)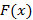 وقتیx
وقتیx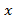 به بینهایت منفی میل می کند عددL است،
به بینهایت منفی میل می کند عددL است، 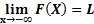 اگر به ازای هر
اگر به ازای هر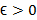 یک عددN وجود داشته باشد بطوری که به ازای هر
یک عددN وجود داشته باشد بطوری که به ازای هر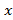 ،
، 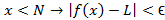 برقرار باشد.
برقرار باشد.
عبارت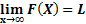 این معنی است که اگر
این معنی است که اگر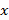 را مثبت و به قدر کافی بزرگ بگیریم،
را مثبت و به قدر کافی بزرگ بگیریم،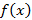 را می توانیم به دلخواه بهL نزدیک کنیم.
را می توانیم به دلخواه بهL نزدیک کنیم.
همچنین عبارت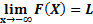 این معنی است که اگر
این معنی است که اگر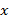 را منفی و به قدر کافی بزرگ (به قدر کافی دور از مبدا در سمت چپ) بگیریم،
را منفی و به قدر کافی بزرگ (به قدر کافی دور از مبدا در سمت چپ) بگیریم،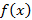 را می توانیم به دلخواه به
را می توانیم به دلخواه به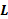 نزدیک کنیم.
نزدیک کنیم.
نابرابری های مذکور در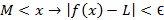 و
و 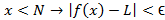 به این معنی هستند که اگر
به این معنی هستند که اگر 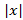 به قدر کافی بزرگ باشد، خم
به قدر کافی بزرگ باشد، خم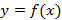 بین خط های
بین خط های 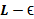 و
و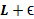 قرار دارد.
قرار دارد.
پیوستگی
توابع پیوسته
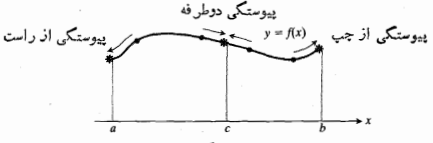
تابعی مانند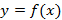 که بتوان نمودار آن را در هربازه ای از دامنه اش با حرکت پیوسته نوک قلم رسم کرد، مثالی از یکتابع پیوسته است. ارتفاع نمودار این تابع در طول بازه به طور پیوسته با x
که بتوان نمودار آن را در هربازه ای از دامنه اش با حرکت پیوسته نوک قلم رسم کرد، مثالی از یکتابع پیوسته است. ارتفاع نمودار این تابع در طول بازه به طور پیوسته با x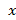 تغییر می کند. در هر نقطه داخلی دامنه تابع، مانند نقطهc مانند شکل زیر مقدار تابع
تغییر می کند. در هر نقطه داخلی دامنه تابع، مانند نقطهc مانند شکل زیر مقدار تابع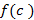 حد مقادیر تابع در هریک از دو طرف است؛ یعنی
حد مقادیر تابع در هریک از دو طرف است؛ یعنی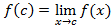 مقدار تابع در هر نقطه انتهایی نیز حد مقادیر تابع در نزدیکی آن
مقدار تابع در هر نقطه انتهایی نیز حد مقادیر تابع در نزدیکی آن
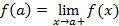 و در نقطه انتهایی راست b ،
و در نقطه انتهایی راست b ،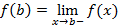
چند تعریف
پیوستگی در یک نقطه داخلی
تابعی چونy=f(x) در یک نقطه داخلی از دامنه اش، مانند c پیوسته است اگر رابطه زیر برقرار باشد.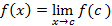
پیوستگی در یک نقطه انتهایی
تابعی چونy=f(x) در یک نقطه انتهایی چپ از دامنه اش، مانند a پیوسته است اگر رابطه زیر برقرار باشد.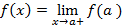
تابعی چونy=f(x) در یک نقطه انتهایی راست از دامنه اش، مانند b پیوسته است اگر رابطه زیر برقرار باشد.
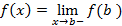
تابع پیوسته
یک تابع پیوسته است اگر در هر نقطه از دامنه اش پیوسته باشد.
نا پیوستگی در یک نقطه
اگر تابعی چونf در نقطه ای مانندc پیوسته نباشد، گوییم کهf درc ناپیوسته است وc را یک نقطه نا پیوستگیf می خوانیم.
آزمون پیوستگی
تابعy=f(x) درx=c پیوسته است اگر و تنها اگر هر سه گزاره زیرصدق کند.
- f(c) وجود دارد (وقتیc در دامنه f است).
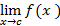 ) وجود دارد (f وقتیx→c دارای حد است).
) وجود دارد (f وقتیx→c دارای حد است).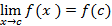 (این حد برابر با مقدار تابع است).
(این حد برابر با مقدار تابع است).
در آزمون پیوستگی، اگرc یک نقطه داخلی دامنهf باشد حد مورد نظر دو طرفه است؛ واگرc یک نقطه انتهایی دامنه باشد، حد مزبور یک حد یک طرفه مناسب(چپ یا راست) است.
نکات مهم پیوستگی
باید بین پیوستگی تابعy=f(x) در x=c و حد داشتن آن تابع وقتیx→c تفاوت قائل شویم. حد،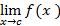 جایی است که وقتیx→c تابع به سوی آن می رود. پیوستگی عبارت استاز این ویژگی که وقتیx عملا بهc می رسدf(x) نیز به نقطه اس که به سویش در حرکت بوده وارد می شود.
جایی است که وقتیx→c تابع به سوی آن می رود. پیوستگی عبارت استاز این ویژگی که وقتیx عملا بهc می رسدf(x) نیز به نقطه اس که به سویش در حرکت بوده وارد می شود.
اگر حد آن چیزی باشد که وقتیx→c انتظارش را دارید، و عدد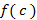 چیزی باشد که درx=c به آن می رسید، آنگاه تابع درc پیوسته است اگر چیزی که انتظارش را دارید با
چیزی باشد که درx=c به آن می رسید، آنگاه تابع درc پیوسته است اگر چیزی که انتظارش را دارید با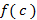 یکی باشد.
یکی باشد.
جهت مظالعه مباحث پیشرفته در زمینه ریاضی یک از محصولکپسول آموزشی ریاضی عمومی 1 سایتلینوم استفاده کنید.