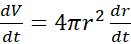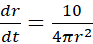نظریه های ماکسیمم و مینیمم
در این مقاله نشان می دهیم که چگونه می توان با استفاده از مشتق نقاطی را به دست آورد که در آن نقاط مقدار تابع مفروض ماکسیمم یا مینیمم باشد.
نسبی در مقابل مطلق
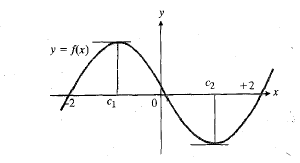
در شکل زیر نقطه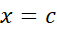 دیده می شود که در آن تابع
دیده می شود که در آن تابع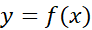 یک مقدار مینیمم دارد. از
یک مقدار مینیمم دارد. از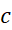 به هر طرف که برویم، خم صعود می کند، و مقدار تابع بزرگتر می شود. اما وقتی به خم دقیق تر نگاه می کنیم، می بینیم که مقدار تابع در
به هر طرف که برویم، خم صعود می کند، و مقدار تابع بزرگتر می شود. اما وقتی به خم دقیق تر نگاه می کنیم، می بینیم که مقدار تابع در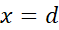
 از آن هم کمتر است. لذا در می یابیم که
از آن هم کمتر است. لذا در می یابیم که 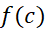 مقدار مینیمم مطلق
مقدار مینیمم مطلق بر
بر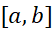 نیست، اما یک مینیمم موضعی یا نسبی آن است.
نیست، اما یک مینیمم موضعی یا نسبی آن است.
تابعی چون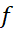 در
در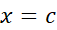 یک مینیمم نسبی یا موضعی دارد هر گاه به ازای همه مقادیر
یک مینیمم نسبی یا موضعی دارد هر گاه به ازای همه مقادیر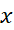 در یک بازه باز حول
در یک بازه باز حول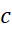 داشته باشیم
داشته باشیم
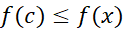
( اگرc یک نقطه انتهایی دامنه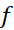 باشد، بازه نیم باز است؛ وc یک نقطه انتهایی آن است.) بازه ممکن است کوچک باشد یا بزرگ، اما در این بازه مقدار تابع هیچگاه از
باشد، بازه نیم باز است؛ وc یک نقطه انتهایی آن است.) بازه ممکن است کوچک باشد یا بزرگ، اما در این بازه مقدار تابع هیچگاه از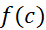 کمتر نیست.
کمتر نیست.
در مورد ماکسیمم نسبی یا موضعی در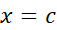 ، به ازای همه مقادیر
، به ازای همه مقادیر 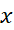 در یک بازه حول
در یک بازه حول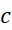 داریم
داریم
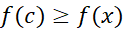
در اینجا واژه نسبی یا موضعی را به کار می بریم تا تمایزی بین این نقطه و یک نقطه ماکسیمم یا مینیمم مطلق قائل شویم. در مورد نقطه ماکسیمم یا مینیمم مطلق به ازای تمام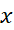 های واقع در یک بازه مناسب حول
های واقع در یک بازه مناسب حول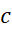 ، داریم
، داریم
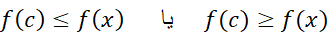
قضیه مشتق اول
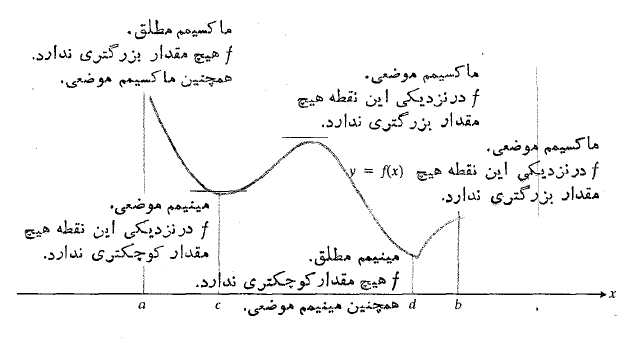
در شکل فوق دو تا از مقادیر اکسترمم تابع به ازای نقاط انتهایی دامنه آن به دست می آیند، یکی هم در نقطه ای قرار دارد که در آن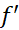 وجود ندارد، و دو تا هم در نقاط داخلی اند که در آن ها'
وجود ندارد، و دو تا هم در نقاط داخلی اند که در آن ها'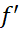 صفر است. معمولا در مورد توابعی که بر یک بازه بسته تعریف می شوند، همین وضع بر قرار است. همان گونه که قضیه زیر می گوید، اگر تابعی در یک نقطه داخلی از دامنه اش یکماکسیممیا یک مینیمم موضعی داشته باشد، و نیز اگر در آنجا مشتق وجود داشته باشد، آنگاه مشتق در آن نقطه باید صفر باشد.
صفر است. معمولا در مورد توابعی که بر یک بازه بسته تعریف می شوند، همین وضع بر قرار است. همان گونه که قضیه زیر می گوید، اگر تابعی در یک نقطه داخلی از دامنه اش یکماکسیممیا یک مینیمم موضعی داشته باشد، و نیز اگر در آنجا مشتق وجود داشته باشد، آنگاه مشتق در آن نقطه باید صفر باشد.
قضیه یک
قضیه مشتق اول برای مقادیر اکسترمم موضعی
فرض کنید تابعی چون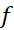 در یک نقطه داخلی مانند
در یک نقطه داخلی مانند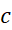 از بازه ای که
از بازه ای که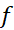 بر آن تعریف می شود، ماکسیمم یا مینیمم موضعی داشته باشد. اگر
بر آن تعریف می شود، ماکسیمم یا مینیمم موضعی داشته باشد. اگر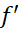 در
در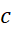 تعریف بشود، آنگاه
تعریف بشود، آنگاه 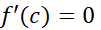
اثبات مثلا فرض کنید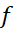 در
در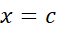 یک مقدار مینیمم موضعی داشته باشد؛ لذا به ازای تمام مقادیر
یک مقدار مینیمم موضعی داشته باشد؛ لذا به ازای تمام مقادیر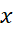 نزدیک
نزدیک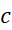 با توجه به شکل زیر داریم
با توجه به شکل زیر داریم
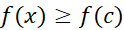
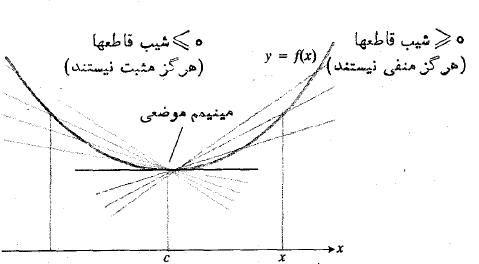
چون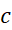 یک نقطه داخلی دامنه
یک نقطه داخلی دامنه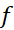 است، می دانیم حد
است، می دانیم حد

که 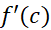 را تعریف می کند، یک حد دو طرفه است. به این معنی است که در
را تعریف می کند، یک حد دو طرفه است. به این معنی است که در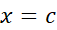 هم حد راست وجود دارد و هم حد چپ، و هر دو برابرند با
هم حد راست وجود دارد و هم حد چپ، و هر دو برابرند با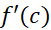 . اگر این حدها را جداگانه بررسی کنیم می بینیم که
. اگر این حدها را جداگانه بررسی کنیم می بینیم که
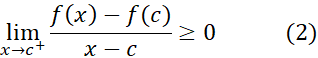
زیرا وقتی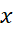 در سمت راست
در سمت راست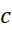 قرار گیرد داریم
قرار گیرد داریم 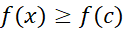 و
و 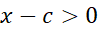 می بینیم که
می بینیم که
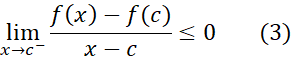
زیرا وقتی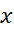 در سمت چپ
در سمت چپ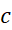 قرار گیرد داریم
قرار گیرد داریم 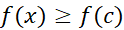 و
و 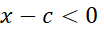 . نا برابری (2) حاکی است که
. نا برابری (2) حاکی است که 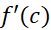 نمی تواند از صفر کوچکتر باشد و نا برابری (3) حاکی است که
نمی تواند از صفر کوچکتر باشد و نا برابری (3) حاکی است که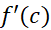 نمی تواند از صفر بزرگتر باشد. پس
نمی تواند از صفر بزرگتر باشد. پس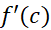 با صفر برابر است.
با صفر برابر است.

وقتی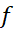 در
در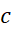 یک مقدار ماکسیمم موضعی داشته باشد، برهان مربوط به
یک مقدار ماکسیمم موضعی داشته باشد، برهان مربوط به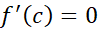 شبیه استدلال فوق است و از آوردن آن صرف نظر می کنیم.
شبیه استدلال فوق است و از آوردن آن صرف نظر می کنیم.
قضیه یک با حذف نقاطی داخلی که در آن ها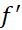 صفر نیست، محل وقوع ماکسیمم ها و مینیمم های موضعی تابع را مشخص می کند. این قضیه حاکی است که با اطمینان می توانیم بررسی خود را به :
صفر نیست، محل وقوع ماکسیمم ها و مینیمم های موضعی تابع را مشخص می کند. این قضیه حاکی است که با اطمینان می توانیم بررسی خود را به :
1.نقاط داخلی که به ازای آن ها'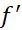 صفر است،
صفر است،
2.نقاطی داخلی که به ازای آن ها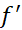 وجود ندارد،
وجود ندارد،
3.نقاط انتهایی دامنه تابع
محدود کنیم. هیچ یک از این نقاط الزاما محل یک ماکسیمم یا مینیمم موضعی نیست، اما این نقاط تنها نامزدهای ممکن اند. نقاطی را که د رآن ها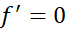 یا'
یا'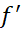 وجود ندارد، عمومانقاط بحرانی
وجود ندارد، عمومانقاط بحرانی می نامند. پس در جستجو برای یافتن مقادیر اکسترمم یک تابع تنها نقاطی که شایسته بررسی هستند، نقاط بحرانی و نقاط انتهایی اند.
می نامند. پس در جستجو برای یافتن مقادیر اکسترمم یک تابع تنها نقاطی که شایسته بررسی هستند، نقاط بحرانی و نقاط انتهایی اند.
تابع های پیوسته بر بازه های بسته
در بیشتر کاربردها، مطلوب ما یافتن مقادیر ماکسیمم یا مینیمم مطلق یک تابع پیوسته بر یک بازه بسته است. لذا ابتدا به این حالت می پردازیم. تعداد نقاطی که این مقادیر را به دست می دهند معمولا چنان کم است که براحتی می توانیم هعرست آن ها را تشکیل دهیم، مقادیر متناظر آن ها را از تابع به دست آوریم، و می بینیم ماکسیمم و مینیمم چه هستند، و در چه نقاطی به دست می آیند.
 مثال 1: مقادیر ماکسیمم و مینیمم مطلق
مثال 1: مقادیر ماکسیمم و مینیمم مطلق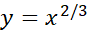 بر بازه
بر بازه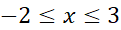 را بیابید.
را بیابید.
حل: مقادیر تابع را در نقاط بحرانی و نقاط انتهایی به دست می آوریم. مشتق اول
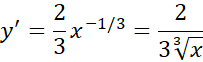
هیچ صفری ندارد، اما در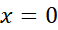 تعریف نمی شوند. به ازای این تنها نقطه بحرانی، و دو نقطه انتهایی دامنه، تابع را محاسبه می کنیم.
تعریف نمی شوند. به ازای این تنها نقطه بحرانی، و دو نقطه انتهایی دامنه، تابع را محاسبه می کنیم.
مقدار در نقطه بحرانی:
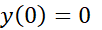
مقادیر در نقاط انتهایی:
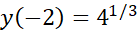
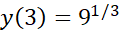
مقدار ماکسیمم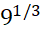 است که به ازای
است که به ازای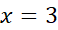 بدست می آید. مینیمم
بدست می آید. مینیمم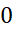 است که به ازای
است که به ازای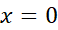 حاصل می شود.
حاصل می شود.
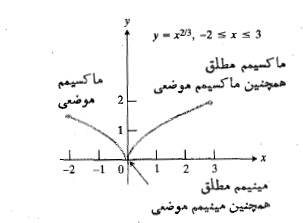
مثال بالا نشان می دهد که وقتی ماکسیمم یا مینیمم در انتهای یک خم قرار گیرد ( انتها صرفا در بازه های محدود وجود دارد) مشتق در چنین نقطه ای الزاما صفر نیست. این مطلب به هیچ وجه قضیه یک را نقض نمی کند. اثبات قضیه ارتباطی با نقاط انتهایی ندارد زیرا لازم است حد خارج قسمت تفاضل های موجود در معادله (1) در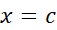 حد دو طرفه باشد تا برهان بعد از آن بتواند اقامه شود.
حد دو طرفه باشد تا برهان بعد از آن بتواند اقامه شود.
بازه های باز یا متناهی : آزمون مشتق دوم
توابعی که بر بازه یا نا متناهی تعریف می شوند ممکن است مقدار ماکسیمم یا مینیمم داشته باشند یا نداشته باشند، و وقتی مقادیر نقاط بحرانی و انتهایی را فهرست کنیم، ممکن است فورا بتوانیم نتیجه گیری کنیم. در چنین موردیحدهای بینهایت تابع ( در صورت وجود) و گاه مشتق دوم تابع را بررسی می کنیم.
 مثال2: مقادیر ماکسیمم و مینیمم تابع
مثال2: مقادیر ماکسیمم و مینیمم تابع
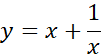
را در صورت وجود بیابید.
حل: می دانیم که این تابع هیچ مقدار ماکسیمم یا مینیمم مطلقی ندارد زیرا وقتی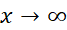 ،
،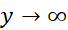 ، و وقتی
، و وقتی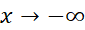 ،
، 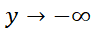 . با وجود این، تابع ممکن است در نقاط انتهایی دامنه ( در این مورد چنین نقاطی وجود ندارند)، و در نقاطی که مشتق اول
. با وجود این، تابع ممکن است در نقاط انتهایی دامنه ( در این مورد چنین نقاطی وجود ندارند)، و در نقاطی که مشتق اول
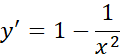
صفر می شود یا وجود ندارد، ماکسیمم یا مینیمم موضعی داشته باشد. از فرمول دیده می شود که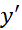 در
در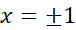 صفر است و در
صفر است و در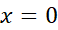 تعریف نمی شود. از
تعریف نمی شود. از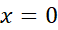 صرف نظر می کنیم زیرا در دامنه تابع قرار نمی گیرد. پس، از مقادیر تابع تنها مقادیر مربوط به نقاط بحرانی
صرف نظر می کنیم زیرا در دامنه تابع قرار نمی گیرد. پس، از مقادیر تابع تنها مقادیر مربوط به نقاط بحرانی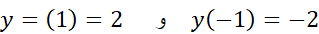 را در نظر می گیریم. اما باید مواظب بود که هرچند -2 از 2 کوچکتر است نباید نتیجه گرفت که -2 یک مینیمم موضعی و 2 یک ماکسیمم موضعی است. در واقع همان گونه که ذیلا نشان می دهیم، درست برعکس است.
را در نظر می گیریم. اما باید مواظب بود که هرچند -2 از 2 کوچکتر است نباید نتیجه گرفت که -2 یک مینیمم موضعی و 2 یک ماکسیمم موضعی است. در واقع همان گونه که ذیلا نشان می دهیم، درست برعکس است.
مشتق دوم
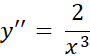
وقتی 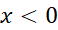 ، منفی است. بنابراین در
، منفی است. بنابراین در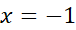 تقعر خم رو به پایین است، و
تقعر خم رو به پایین است، و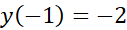 یک مقدار ماکسیمم موضعی است. همچنین، وقتی
یک مقدار ماکسیمم موضعی است. همچنین، وقتی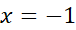
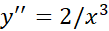 مثبت است، و لذا تقعر خم در
مثبت است، و لذا تقعر خم در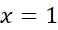 رو به بالا است، و
رو به بالا است، و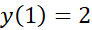 یک مقدار مینیمم موضعی است. پس مقدار مینیمم موضعی از مقدار ماکسیمم موضعی بزرگتر است.
یک مقدار مینیمم موضعی است. پس مقدار مینیمم موضعی از مقدار ماکسیمم موضعی بزرگتر است.
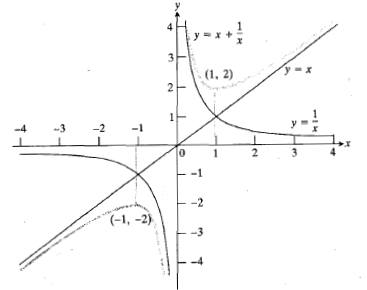
آزمونمشتق دوم که غالبا برای بررسی نقاطی که در آن ها مشتق اول صفر است به کارمی رود به شرح زیر است.
آزمون مشتق دوم برای ماکسیمم ها و مینیمم های موضعی
اگر 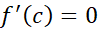 و
و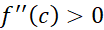 ، آنگاه
، آنگاه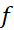 در
در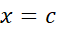 یک ماکسیمم موضعی دارد.
یک ماکسیمم موضعی دارد.
اگر 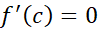 و
و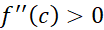 ، آنگاه
، آنگاه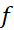 در
در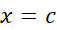 یک ممینمم موضعی دارد.
یک ممینمم موضعی دارد.
 مثال3 : تمام ماکسیمم ها و مینیمم های تابع زیر را بیابید.
مثال3 : تمام ماکسیمم ها و مینیمم های تابع زیر را بیابید.
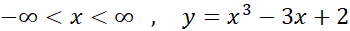
حل: دامنه هیچ نقطه انتهایی ندارد،و تابع در همه نقاط مشتق پذیر است. پس مقادیر اکسترمم تنها به ازای نقاطی به دست می آیند که در آن ها مشتق
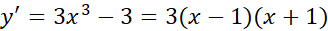
صفر است؛ این نقاط عبارت اند از 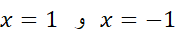 . مشتق دوم
. مشتق دوم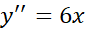 در
در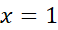 مثبت و در
مثبت و در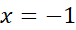 منفی است. پس
منفی است. پس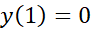 یک مقدار مینیمم موضعی است و
یک مقدار مینیمم موضعی است و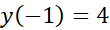 یک مقدار ماکسیمم موضعی است.
یک مقدار ماکسیمم موضعی است.
کنار گذاشتن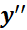
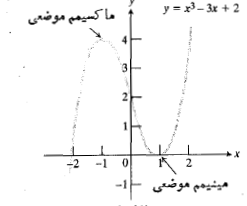
در مثال 3 اگر به چگونگی تغییر علامت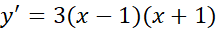 وقتی
وقتی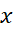 زیاد می شود توجه کنیم شکل زیر دیگر به آزمون مشتق دوم نیازی نداریم. تغییر علامت
زیاد می شود توجه کنیم شکل زیر دیگر به آزمون مشتق دوم نیازی نداریم. تغییر علامت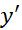 از + به – درx=-1 ، بر وجود مقدار ماکسیمم موضعی در
از + به – درx=-1 ، بر وجود مقدار ماکسیمم موضعی در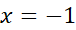 دلالت دارد. به همین ترتیب، تغییر علامت'
دلالت دارد. به همین ترتیب، تغییر علامت'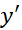 از – به + در
از – به + در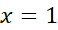 حکایت می کند.
حکایت می کند.
اگر یافتن مشتق دوم تابعی مشکل باشد یا اگر پس از محاسبه مشتق دوم کار کردن با آن آسان نباشد، شاید بررسی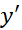 و تعیین تغییر علامت راه بهتری باشد. در واقع وقتی یافتن تغییرات علامت
و تعیین تغییر علامت راه بهتری باشد. در واقع وقتی یافتن تغییرات علامت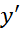 آسان است، ممکن است محاسبه
آسان است، ممکن است محاسبه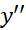 اصلا لزومی نداشته باشد.
اصلا لزومی نداشته باشد.

آهنگ های تغییر وابسته
وقتی هوا با آهنگ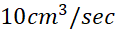 به یک حباب کروی صابون دمیده می شود، شعاع حباب با چه سرعتی تغییر می کند؟ وقتی آب یک مخزن استوانه ای با آهنگ 3 لیتر بر ثانیه تخلیه می شود، سطح آب با چه سرعتی پایین می رود؟
به یک حباب کروی صابون دمیده می شود، شعاع حباب با چه سرعتی تغییر می کند؟ وقتی آب یک مخزن استوانه ای با آهنگ 3 لیتر بر ثانیه تخلیه می شود، سطح آب با چه سرعتی پایین می رود؟
با دانستن آهنگ تغییر یک متغیر چگونه می توانآهنگ تغییر دیگری را محاسبه کرد. برای محاسبه اهنگ مجهول، معادله ای می نویسیم که این دو متغیر را به هم ربط دهد و سپس از آن مشتق می گیریم تا معادله ای به دست آید که آهنگ مطلوب را به آهنگ معلوم مربوط کند.
 مثال 1: وقتی هوا با آهنگ/sec
مثال 1: وقتی هوا با آهنگ/sec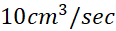 به یک حباب کروی صابون دمیده می شود، شعاع حباب با چه سرعتی تغییر می کند؟
به یک حباب کروی صابون دمیده می شود، شعاع حباب با چه سرعتی تغییر می کند؟
حل: آهنگ تغییر حجم به ما داده شده است و می خواهیم آهنگ تغییر شعاع را بیابیم.
حجم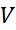 و شعاع
و شعاع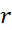 را به صورت توابع مشتق پذیری از زمان
را به صورت توابع مشتق پذیری از زمان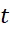 در نظر می گیریم. مشتقات
در نظر می گیریم. مشتقات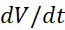 و
و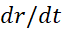 به ترتیب آهمگ تغییر
به ترتیب آهمگ تغییر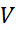 و
و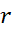 را به دست می دهند. بنا به فرض داریم
را به دست می دهند. بنا به فرض داریم
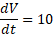
مطلوب ما دانستن مقدار ( با چه سرعتی شعاع تغییر می کند؟) 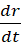 است. برای پاسخ گویی به این سوال، ابتدا معادله ای می نویسیم که
است. برای پاسخ گویی به این سوال، ابتدا معادله ای می نویسیم که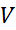 و
و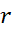 را به هم مربوط کند.
را به هم مربوط کند.
- (حباب کروی است.)
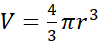
حال اگر از دو طرف معادله نسبت بهt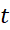 مشتق بگیریم معادله ای به دست می آوریم که
مشتق بگیریم معادله ای به دست می آوریم که 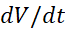 و
و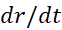 را به هم مربوط می کند
را به هم مربوط می کند
مقدار معلوم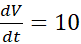 را در معادله می گذاریم و
را در معادله می گذاریم و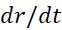 را محاسبه می کنیم
را محاسبه می کنیم
از معادله (3) بر می آید که آهنگ تغییر در هر زمان مشخص به بزرگی
در هر زمان مشخص به بزرگی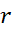 در آن لحظه بستگی دارد. وقتی
در آن لحظه بستگی دارد. وقتی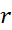 کوچک باشد،
کوچک باشد، 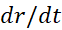 بزرگ است؛ و وقتی
بزرگ است؛ و وقتی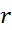 بزرگ باشد،
بزرگ باشد،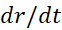 کوچک خواهد بود.
کوچک خواهد بود.
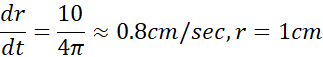
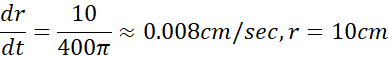
قضیه مقدار میانگین
در حساب دیفرانسیل و انتگرال کمتر قضیه ای به اندازه قضیه مقدار میانگین و تعمیم هایش کار ساز است. صورت این قضیه چنان ساده است که در بدو امر کسی متوجه اهمیت نتایج عدیده آن نمی شود.
این قضیه، ریاضیات لازم را برای برآورد کردن مقدار خطای ناشی از تقریب زدن خطی در اختیار ما می گذارد؛ آزمونمشتق اول برای صعودی و نزولی بودن را توضیح می دهد؛ با نشان دادن این مطلب که توابع ثابت تنها توابعی هستند که مشتقشان صفر است، راه حساب انتگرال را می گشاید.
راه ورود به قضیه مقدار میانگین، صورت اولیه آن است که قضیه رول نام دارد.
قضیه رول
شواهد هندسی محکمی در دست است که اگر خم همواری محور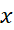 را در آن، مماس بر خم افقی مانند شکل زیر است.
را در آن، مماس بر خم افقی مانند شکل زیر است.
قضیه 2
قضیه رول
فرض کنید که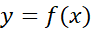 در هر نقطه از بازه بسته
در هر نقطه از بازه بسته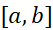 پیوسته، و در هر نقطه از بازه باز
پیوسته، و در هر نقطه از بازه باز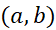 مشتق پذیر باشد. اگر
مشتق پذیر باشد. اگر
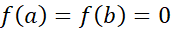
آنگاه دست کم یک نقطه مانند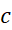 بین
بین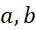 وجود دارد که در آن
وجود دارد که در آن 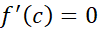 است.
است.
اثبات قضیه رول
می دانیم تابع پیوسته ای که بازه بسته ای تعریف شده باشد، بر آن بازه مقادیر ماکسیمم و مینیمم دارد، و نیز می دانیم که این مقادیر تنها به ازای نقاط انتهایی و نقاط بحرانی به دست می آیند.
در مورد تابع مورد نظر ما این نقاط عبارت اند از نقاط انتهایی و آن نقاط داخلی که به ازای آن هاf'صفر است. پس، اگر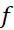 در یک نقطه داخلی مانندc ماکسیمم یا مینیمم بشود، آنگاه
در یک نقطه داخلی مانندc ماکسیمم یا مینیمم بشود، آنگاه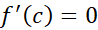 است.
است.
اگر این تابع به ازای نقاط انتهایی هم ماکسیمم شود، و هم مینیمم، آنگاه صفر هم مقدار ماکسیمم و هم مقدار مینیمم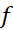 است. بنابراین به ازای تمام
است. بنابراین به ازای تمام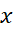 های موجود در
های موجود در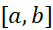 ،
، 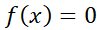 ، و
، و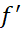 به ازای همه مقادیر
به ازای همه مقادیر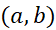 صفراست زیرا
صفراست زیرا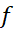 ثابت است.
ثابت است.
در هر حال، در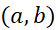 دست کم یک نقطه می یابیم که در آن
دست کم یک نقطه می یابیم که در آن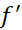 صفر است.
صفر است.
 مثال: چند جمله ای
مثال: چند جمله ای 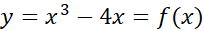
به ازای تمام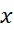 ها،
ها،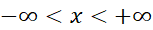 ، پیوسته و مشتق پذیر است. اگر فرض کنیم
، پیوسته و مشتق پذیر است. اگر فرض کنیم 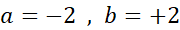
فرض های قضیه رول بر قرارخواهند بود زیرا 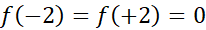
پس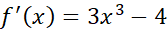 باید بین 2- و 2+ دست کم یک بار صفر شود. در عمل می بینیم که در
باید بین 2- و 2+ دست کم یک بار صفر شود. در عمل می بینیم که در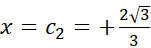 و
و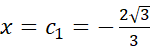
داریم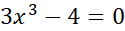 .
.
نکته : همان گونه که شکل زیر نشان می دهد، مشتق پذیر بودن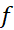 بر
بر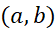 اساس قضیه رول است. اگر
اساس قضیه رول است. اگر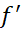 حتی در یک نقطه وجود نداشته باشد، ممکن است خم هیچ مماس افقی نداشته باشد.
حتی در یک نقطه وجود نداشته باشد، ممکن است خم هیچ مماس افقی نداشته باشد.
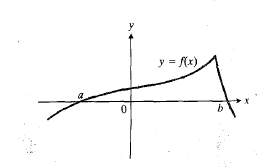
قضیه مقدار میانگین
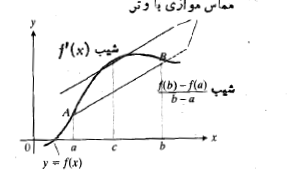
قضیه مقدار میانگین همان قضیه رول است که در آن، وتر بجای بازه قرار می گیرد. مانند شکل زیر، این شکل نمودار تابع مشتق پذیری را نشان می دهد که بر بازه ای چون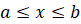 تعریف شده است. نقطه ای روی خم وجود دارد که مماس در آن نقطه با وتر
تعریف شده است. نقطه ای روی خم وجود دارد که مماس در آن نقطه با وتر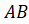 موازی است. در قضیه رول خط
موازی است. در قضیه رول خط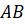 محورx
محورx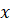 است و
است و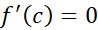 .
.
در اینجا خط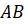 وترمار بر نقاط انتهایی خم است که در بالای
وترمار بر نقاط انتهایی خم است که در بالای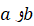 قرار دارند، و
قرار دارند، و
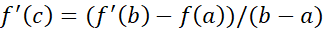 .
.
قضیه 3
قضیه مقدار میانگین
اگر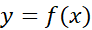 در هر نقطه از بازه بسته
در هر نقطه از بازه بسته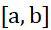 پیوسته و در هر نقطه از بازه باز
پیوسته و در هر نقطه از بازه باز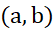 مشتق پذیر باشد،آنگاه دست کم یک نقطه چون
مشتق پذیر باشد،آنگاه دست کم یک نقطه چون 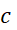 بین
بین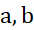 وجود دارد که
وجود دارد که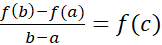 .
.
جهت استفاده از مباحث بیشتر از محصول کپسول آموزشی ریاضی عمومی 1 در سایت لینوم استفاده نمایید.