تابع های چند جمله ای و مشتق آن ها

تعریف مشتق

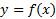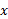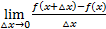
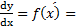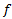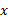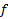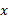فرض کنید تابعی از باشد. اگرحد      موجود و متناهی باشد، این حد را مشتق در می نامیم و می گوییم در مشتق پذیر است.

می توان به شکل خلاصه به جای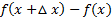 از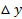 استفاده کنیم. به این صورت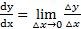

قاعده یک

مشتق عدد ثابت صفر است. قاعده یک حاکی از این است که اگر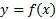 دارای مقدار ثابت c باشد، آنگاه 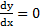، دلیل درستی این قاعده، محاسبه زیر است.

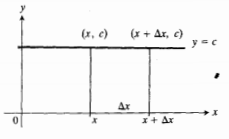
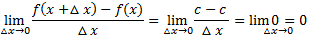
قاعده دو

قاعده توان برای توان های صحیح و مثبتx

اگرn یک عدد صحیح مثبت باشد، آنگاه 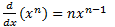 برقرار است. روش استفاده از قاعده توان این است که از توان اولیه (n) یک را می کاهیم و حاصل را درn ضرب می کنیم.

قاعده سه

قاعده ضریب (ثابت)

اگرu تابع مشتق پذیری ازx ، وc عدد ثابتی باشد، آنگاه 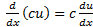      ، قاعده سه حاکی است که مشتق حاصل ضرب یک عدد در یک تابع برابر است با حاصلضرب آن عدد در مشتق آن تابع.

قاعده چهار

قاعده مجموع

اگرu وv تابع های مشتق پذیری ازx باشند آنگاه مجموع آن ها 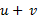  ، نیز تابع مشتق پذیری ازx است و برای هر مقداری ازx که به ازای آن مشتقu و مشتق 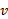هر دو وجود داشته باشند، داریم:   .

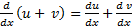به همین ترتیب، مشتق مجموع هر تعداد متناهی تابع مشتق پذیر، برابر است با مجموع مشتقات آنتابع ها.

نکته این است که اگرu وv هر دو درx مشتق  داشته باشند، آنگاه مجموع آن ها نیز درx مشتق دارد و مقدار آن برابر است با مجموع مشتق هایu وv درx .

مشتق های دوم

مشتق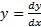        

مشتق اولy نسبت به  x است. مشتق اول خود تابعی ازx است و ممکن است مشتق پذیر باشد. اگر چنین باشد، مشتق آن، یعنی: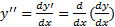 

را مشتق دومy نسبت بهx می نامند.

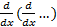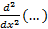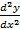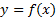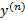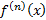عمل دوبار مشتق گیری متوالی از یک تابع را با   یا  نمایش می دهند، با این نماد، مشتق دومy نسبت بهx به صورت  می نویسند. در حالت کلی، نتیجه n  بار مشتق گیری متوالی از تابعی چون را با ، ، یا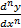  نمایش می دهند.

قاعده پنجم

قاعده حاصل ضرب ها

حاصل ضرب دو تابع مشتق پذیرu وv ، مشتق پذیر است و داریم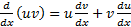     

این قاعده حاکی است که به ازای چنین x هایی مشتق حاصل ضربuv برابر است باu ضربدر مشتقv ، به علاوهv ضربدر مشتقu.

قاعدع ششم

توان های صحیح مثبت یک تابع مشتق پذیر

اگرuتابع مشتق پذیری ازx وn عدد صحیح مثبتی باشد، آنگاه "u     مشتق پذیر است و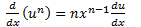   

قاعده هفتم

قاعده خارج و قسمت

خارج و قسمت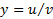 از دو تابع مشتق پذیر در نقطه ای که  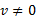 مشتق پذیر است و داریم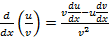   

قاعده هشتم

توان های صحیح منفی

اگر به جای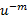 بنویسیم 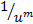، می توانیم قاعده خارج قسمت را به کار بریم و نشان دهیم که قاعده مشتق گیری از توان های صحیح مثبت برای توان های صحیح منفی هم برقرار است.

توان های صحیح منفی یک تابع مشتق پذیر

در نقطه ای کهu مشتق پذیر باشد و صفر نباشد، مشتق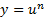 وقتی کهn یک عدد صحیح منفی باشد از

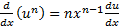   بدست می آید.

مشتق گیری ضمنی و توان های کسری

وقتی معادله ای بر حسب x و  y ،y   را به عنوان تابعی مشتق پذیر از x تعریف کند، حتی در مواردی که نتوان y را از معادله  ای بدست آورد ، اغلب می توان با استفاده ازقواعد مشتق گیری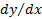 را محاسبه کرد.

مشتق گیری ضمنی

بیشتر توابعی که بررسی شد، معادلاتی داشتند که y را به طور صریح بر حسب x بیان می کردند. اما غالبا به معادلاتی نظیر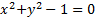 و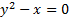 بر می خوریم که y را بطور صریح بر حسب x  به دست نمی دهند. در عین حال هریک از این معادلات رابطه ای بین  y و x  تعریف می کنند. وقتی عدد معینی از دامنه مناسبی به جای x  قرار گیرد، معادله حاصل یک یا چند مقدار برای y به دست می دهد. می توان جفت های y  و x حاصل را در صفحه مشخص و نمودار معادله را رسم کرد.

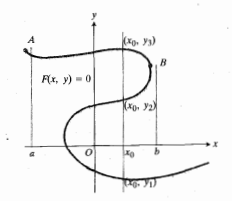
نموار معادله دلخواهی چون 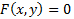 بر حسب x و y  ممکن است نمودار تابعی مانند 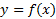نباشد، زیرا شاید برخی از خطوط قائم آن را بیش از یک بار قطع کنند. مثلا در شکل زیر اعداد 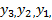همه متناظر با مقدار 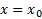هستند. جفت های 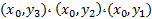همه در معادله 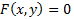صدق می کنند و نقاط متناظر بر نمودار  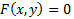 قرار می گیرند.

با وجود این، بخش های مختلفی از خم 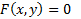 می توانند نمودار توابعی از 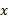باشند. مثلا قسمت AB از خم موجود در شکل زیر نمودار تابعی چون 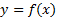 است که در 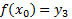صدق می کند و بر بازه باز 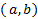که شامل 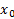است تعریف می شود. اگر 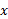 نقطه دلخواهی از 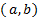باشد، آنگاره جفت 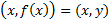در معادله اصلی  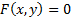  صدق می کند. می گوییم که معادله 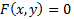به طور ضمنی 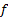را بر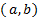 تعریف می کند، هرچند از روی آن 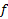به طور صریح به صورت 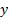بر حسب 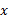به دست نیاید.

توان های کسری

با استفاده از مشتق گیری ضمنی می توانیم قاعده توان را تعمیم دهیم تا نماهای کری را هم شامل بشود.

قاعده نهم

قاعده توان برای نماهای کسری

اگر u تابع مشتق پذیری از x باشد، qو p و  (q>0) اعداد صحیحی باشند، با این شرط که وقتی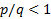  آنگاه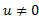 ، داریم:

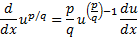
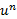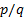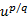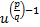این همان قاعده آشنا برای محاسبه مشتق  است که تعمیم داده شد تا n بتواند هرعدد گویایی مانند  باشد. مانند قواعد قبلی، معادله بالا تنها برای مقادیری از x برقرار است که به ازای آن ها   و   و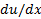   اعداد حقیقی باشند. لذا قاعده 9 حاکی است که با محاسبه طرف راست معادله بالا در x ، می توانیم مقدار مشتق 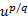 را در x بدست آوریم.

تقریب خطی ودیفرانسیل

خطی سازی

همانگونه که در شکل زیر دیده می شود، مماس بر خمی چون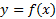  در حوالی نقطه تماس نزدیک خم قرار می گیرد، و در بازه کوچکی که در هر دو طرف نقطه امتداد دارد، مقادیر y روی خط مماس تقریب های خوبی برای مقادیر y خم هستند. لذا پیشنهاد می شود روی این بازه به جای فرمولf  ، فرمول خط مماس آن را قرار دهید.

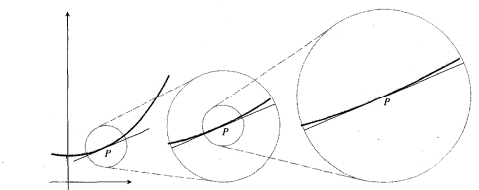
در شکل زیر مماس از نقطه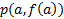  می گذرد و شیب آن 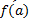 است. لذا معادله نقطه شیب آن

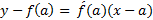
یا

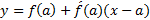
است. پس خط مماس، نمودار تابع 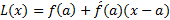  است.

درمکان هایی که این خط نزدیک نمودارf باشد،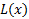  تقریب خوبی از 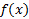 است.

تابع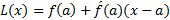  را صورت خطی شده  f در a  می نامیم. تقریب  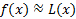 ، تقریب خطی متداول  f در a  است.

تعریف صورت خطی و تقریب خطی متداول

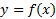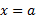اگر  در  مشتق پذیر باشد، آنگاه  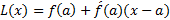  را صورت خطی شده  f در a  می نامند. تقریب 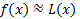 تقریب خطی متداول f در a  نام دارد.

قاعده زنجیری

قاعدع محاسبه مشتق ترکیب دو تابع مشتق پذیر، بطور خلاصه این است که مشتق این ترکیب برابر است با حاصل ضرب مشتقات دو تابع. این قاعده را قاعده زنجیری می نامند. چون اغلب توابعی که در عمل به کار می روند ترکیب توابع دیگر، شاید قاعده زنجیری بیش از سایر قواعد در مشتق گیری به کار می رود.

مثال تابع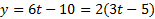  از ترکیب 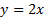 و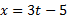  به دست می آید. چه ارتباطی بی مشتق های این سه تابع وجود دارد؟

حل: داریم

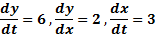
چون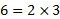   پس

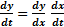
قاعده زنجیری(صورت اول)

فرض کنید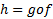  ترکیب تابع های مشتق پذیر 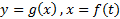  را نمایش دهد. آنگاهh تابع مشتق پذیری ازt است که مشتقش به ازای هر مقدارt برابر است با

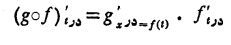
بطور خلاصه به ازای هر مقدارt

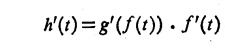
معادلات بالا بیان می کنند که هر مشتق را چگونه محاسبه کنیم، سپس می توانیم مشتق را از معادله زیر نیز بدست آوریم.

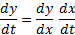
اگر y تابع مشتق پذیری از x و x تابع مشتق پذیری ازt باشد، آنگاه y تابع مشتق پذیری ازt استو مشتق آن از معادله زیر بدست می آید.

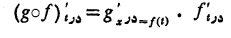
قاعد زنجیری(صورت خلاصه)

اگر y تابع مشتق پذیری از x و x تابع مشتق پذیری ازt باشد، آنگاه y تابع مشتق پذیری ازt است و داریم:   .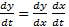

اثبات قاعده زنجیری

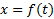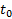اگر  در  مشتق پذیر باشد، آنگاه 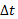نمو   نمو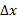  را به وجود می آورد به قسمی که

(الف)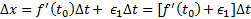  

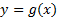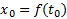و اگر  در  مشتق پذیر باشد، آنگاه 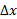نمو  نمو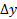  را تولید م یکند به قسمی که

(ب)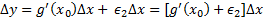   

در معادلات (الف و ب) وقتی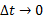  ،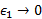   و وقتی 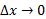 ، 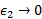 . از ترکیب معادلات (الف و ب) نتیجه می شود:

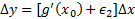
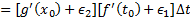
دو طرف را بر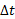  تقسیم می کنیم و نتیجه می گیریم:

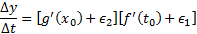
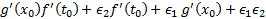
وقتی که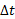  به صفر میل می کند، 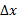، 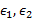 به صفر میل کی کنند و داریم:  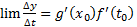   که همان 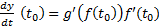    است.

مثال: اگر 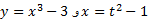  ,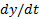  را بر حسب t بیان کنید.

حل: از قاعده زنجیری نتیجه می گیریم که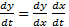    

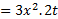
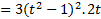
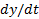(  را در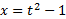  محاسبه کرده ایم)

مروری مختصر بر مثلثات

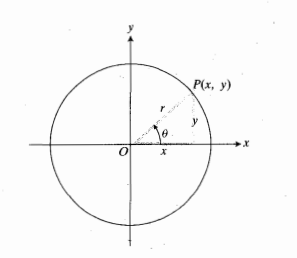
وقتی زاویه ای به اندازه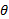  شکل زیر در مرکز دایره ای به شعاع r در وضع متداول قرار گیرد،توابع مثلثاتی 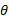 با معادلات زیر تعریف می شوند.

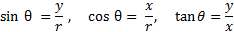
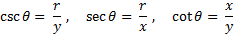
مشاهده می کنید که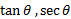   برای مقادیری از 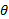 که به ازای آن ها 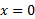 ، تعریف نمی شوند. به این معنی که 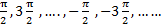  بر حسب رادیان از دامنه توابع تانژانتی و سکانتی حذف می شوند. به همین ترتیب، 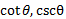 برای  مقادیر 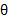 ی متناظر با 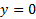 یعنی برای.  تعریف نمی شوند.

برای مقادیری از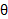  که این توابع تعریف می شوند، بنابر معادلات بالا داریم:

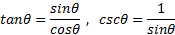
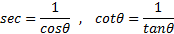
چون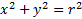   بنابر قضیه فیثاغورس داریم:

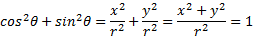
بنابر شکل بالا مختصات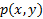  را هم بر حسب   و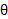   بیان می کنیم.

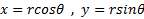
از شکل برمی آید که وقتی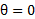 ، داریم  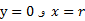   در نتیجه بنابر تعریف

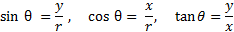
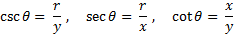
  نتیجه می گیریم:

به همین ترتیب در مورد زاویه قائمه   داریم 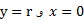     لذا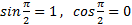

محاسبه سینوس و کسینوس

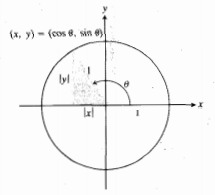
اگر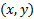  نقطه ای روی دایره ای به شعاع  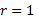 واحد باشد، آنگاه معادلات  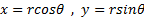  به صورت 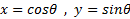 در می آیند. بنابراین کسینوس و سینوس هر زاویه ای را می توان از مثلث حاده مرجع محاسبه کرد. این مثلث طبق شکل زیر با رسم خطی عمود بر محورx تشکیل می شود. نسبت ها از مثلث به دست می آیند و علامت ها به ربعی که زاویه در آن قرار می گیردبستگی دارد.

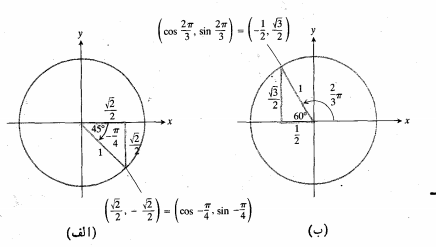
مثال : بنا به شکل زیر حالت (الف) یعنی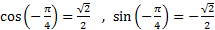

حالت (ب) یعنی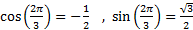                                         

 اندازه رادیانی               

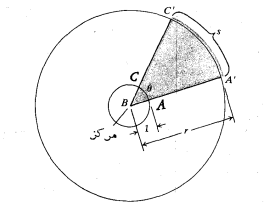
اندازه رادیانی زاویه 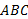  که راس آن B، مرکز دایره واحد شکل زیر است. بنا به تعریف عبارت است از 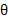 ، یعنی طول قوس مستدیر 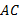. اگر این زاویه از دایره دیگری به مرکز Bقوس 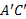 را جدا کند، آنگاه قطاع های مستدیر 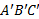 و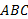  با هم متشابه اند. در نتیجه نسبت طول قوس به شعاع یکی از آن دو، با نسبت نظیرش از دیگری مساوی است.

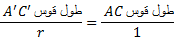
یا

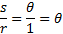
این رابطه صرف نظر از بزرگی یا کوچکی شعاع دایره دوم درست است. پس در مورد هر دایره ای که مرکزشB باشد، نسبت طول قوس جدا شده به شعاع دایره،s/r، همواره اندازه رادیانی زاویه را بدست می دهد.

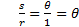  گاه بصورت 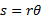 هم می نویسند. این صورت معادله برای محاسبه طول قوس  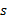 وقتی که شعاع r و اندازه رادیانی زاویه معلوم باشند مناسب است.

در این مقاله ازسایت لینوم در مورد مشتقات و کاربرد آن ها و همچنین قاعده زنجیری، تقریب خطی و دیفرانسیل، مشتق گیری ضمنی، توان کسری صحبت شد. توصیه می کنیم جهت یاد گیری مباحث بیشتراز محصول کپسول آموزشی ریاضی 1 استفاده کنید.