معادله لاگرانژ و معادلات دیفرانسیل مرتبه دوم
در این آموزش معادلات دیفرانسیل لینوم، به سراغ یادگیری معادله لاگرانژ و معادلات دیفرانسیل مرتبه دوم و بالاتر میرویم.
معادله لاگرانژ
فرم کلی این معادله به صورت زیر میباشد:
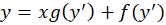
اگرمعادله کلرو را به یاد داشتهباشید متوجه میشوید،معادله لاگرانژ صورت تعمیمیافتهمعادله کلرو است.
روش حل معادله لاگرانژ
برای حل این معادله از روش
که پیش از این به آن اشاره کردهبودیم، استفاده میکنیم.معادله کلرو نیز به سادگی با این روش قابل حل میباشد.
مثال) معادله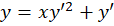
را حل کنید.
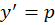قرار میدهیم و سپس از طرفین دیفرانسیل میگیریم و به جای
،
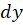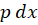قرار میدهیم:
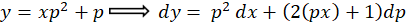
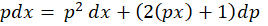
معادله را بر حسب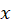 
مرتب میکنیم:
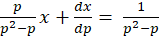
و در نهایت معادله فوق به شکل زیر حل میشود:
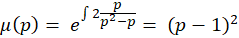
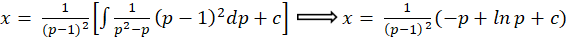
اگر امکانش وجود داشت، از جواب نهایی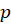
را حذف کنید وگرنه آن را به همین صورت رها کنید.
معادلات دیفرانسیل مرتبه دوم و بالاتر
این دسته از معادلات هم مانندمعادلات مرتبه اول شکلهای مختلف و روشهای حل متفاوتی دارند که در ادامه به بررسی آنها میپردازم:
معادلات دیفرانسیلی با مرتبه دو و بیشتر که قابل تبدیل به معادلات مرتبه اول هستند
پیش از این که روشهایی که به طور خاص برای حل معادلات مرتبه دوم و بالاتر به کار میرود را بیان کنیم، باید قابل تبدیل بودن آن معادله به یک معادله مرتبه اول را بررسی کنیم.معادلات دیفرانسیلی مرتبه دوم که قابل تبدیل به معادلات مرتبه اول هستند عبارتند از:
1-معادلات دیفرانسیل مرتبه دوم که فاقد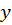
،
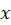یا هر دو هستند.
فرم کلی معادلاتی که فاقد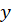
هستند به صورت 
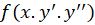است و برای حل آنها باید 
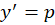قرار دهیمو در نتیجه 
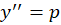است.صورت کلی معادلاتی که فاقد
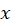هستند، به شکل
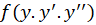است و روش حل آنها نیز مشابه معادلات فاقد
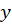است یا یک تفاوت. یعنی در ابتدا باید
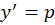قرار دهیم؛ اما در قدم بعدی توجه کنید که
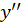را برابر با
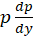قرار دهید. برای حل معادلاتی که فاقد
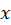و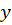
هستند نیز تنها کافیست قرار دهید
.
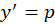مثال) معادله
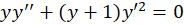را حل کنید.
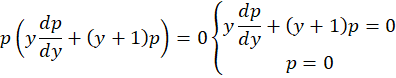
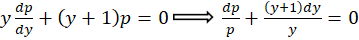
به یک معادله جدا شدنی رسیدیم:
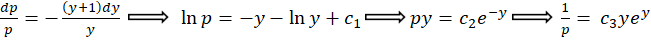
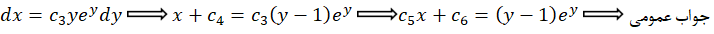
جواب عمومی معادله را بهدست آوردیم و حالا با توجه به دستگاه ابتدایی میتوانیم یک جواب خصوصی معادله را نیز تعیین کنیم:
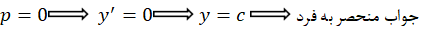
2-معادله به فرم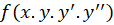
همگن است هر گاه داشتهباشیم:
)
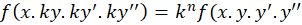این معادلات با تغییر متغیر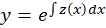
بهمعادله مرتبه اول تبدیل میشود:
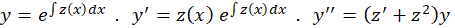
مثال) معادله دیفرانسیل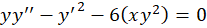
را حل کنید.
)
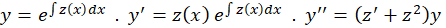
این عبارات را در معادله جایگذاری میکنیم:
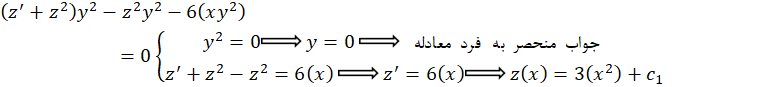
و در نهایت جواب عمومی معادله را بهدست می آوریم:
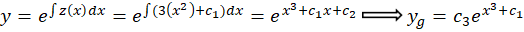
قضایای معادلات دیفرانسیل خطی مرتبه دوم
معادله دیفرانسیل خطی مرتبه دوم به فرم کلی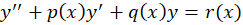
است و برای این معادله قضایای زیر را بیان میکنیم:
1-معادله فوق در صورتی همگن است که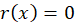
. اگر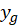
جواب عمومی معادله فوق در حالت همگن شده و
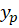جواب خصوصی آن در حالتهمگن شدهباشند در این صورت جواب عمومی معادله در حالت غیرهمگن
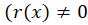برابر است با:
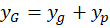
2-اگر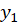
و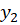
دو جواب معادله ازمعادله دیفرانسیل
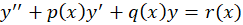در حالت همگن شده
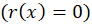باشند آنگاه ترکیب خطی این دو جواب (
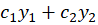) نیز یک جواب این معادله در حالت همگن شدهاست.
3- اگر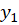
و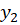
دو جواب مستقل خطی از معادله دیفرانسیل
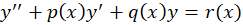در حالت همگن شده
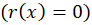باشند آنگاه ترکیب خطی این دو جواب (2
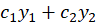) جواب عمومی این معادله در حالت همگن شدهاست.در ادامه با مفاهیم استقلال خطی آشنا خواهیم شد.
برای تسلط بیشتر بر این مباحث، میتوانید کپسول آموزشی معادلات دیفرانسیل لینوم را مشاهده کنید.