معادله دیفرانسیل کامل

در اینآموزش معادلات دیفرانسیللینوم، به سراغ یادگیریمعادلات دیفرانسیل کامل میرویم.
تعریف
معادله دیفرانسیلی 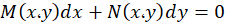 را یک معادله کامل گویند هرگاه تابعی مانند
را یک معادله کامل گویند هرگاه تابعی مانند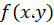 وجود داشتهباشد که به ازای آن دو رابطه زیر برقرار باشد:
وجود داشتهباشد که به ازای آن دو رابطه زیر برقرار باشد:
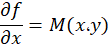
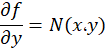
روش بررسی کامل بودن یک معادله دیفرانسیلی
اگر عبارتهای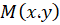 ،
،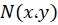 ،
،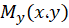 و
و بر روی ناحیهای از صفحه مانند
بر روی ناحیهای از صفحه مانند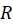 پیوسته باشند،معادله دیفرانسیل
پیوسته باشند،معادله دیفرانسیل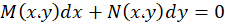 کامل است اگر و تنها اگر:
کامل است اگر و تنها اگر:
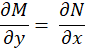
روش حل معادلات دیفرانسیل کامل
در صورتی که معادله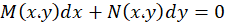 کامل باشد میدانیم تابعی به نام
کامل باشد میدانیم تابعی به نام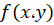 وجود دارد که جواب معادله است و به ازای آن دو رابطه
وجود دارد که جواب معادله است و به ازای آن دو رابطه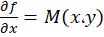 و
و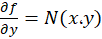 برقرار است،
برقرار است،
برای بهدست آوردن تابع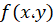 میتوان از هر کدام از روابط فوق استفاده کرد ولی توصیه ما شروع از رابطهای است که انتگرالگیری نسبت به متغیر آن سادهتر است، در این جا ما فرض کردیم انتگرالگیری نسبت به متغیر
میتوان از هر کدام از روابط فوق استفاده کرد ولی توصیه ما شروع از رابطهای است که انتگرالگیری نسبت به متغیر آن سادهتر است، در این جا ما فرض کردیم انتگرالگیری نسبت به متغیر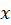 سادهتر است پس داریم:
سادهتر است پس داریم:
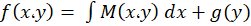
از آنجایی که انتگرال نسبت به متغیر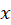 گرفته شد پس متغیر
گرفته شد پس متغیر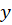 در رابطه بالا ثابت در نظر گرفتهشده و عدد ثابت خروجی از انتگرال را میتوان تابعی بر حسب
در رابطه بالا ثابت در نظر گرفتهشده و عدد ثابت خروجی از انتگرال را میتوان تابعی بر حسب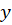 در نظر گرفت، در ادامه برای بهدستآوردن تابع
در نظر گرفت، در ادامه برای بهدستآوردن تابع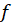 باید تابع
باید تابع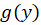 را نیز بهدست آوریم.برای اینکار از رابطه بالا مشتق گرفته و آن را برابر با
را نیز بهدست آوریم.برای اینکار از رابطه بالا مشتق گرفته و آن را برابر با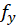 قرار میدهیم و بدین ترتیب
قرار میدهیم و بدین ترتیب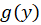 بهدست میآید.
بهدست میآید.
جواب عمومی نهایی این معادله برابراست با : 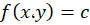
 مثال) معادله دیفرانسیل
مثال) معادله دیفرانسیل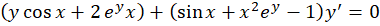 را حل کنید.
را حل کنید.
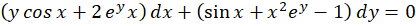
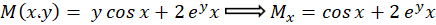
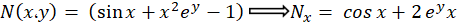
با توجه به اینکه 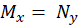 پس معادله کامل است و داریم:
پس معادله کامل است و داریم:
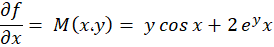
از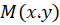 نسبت به متغیر
نسبت به متغیر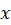 انتگرال میگیریم:
انتگرال میگیریم:
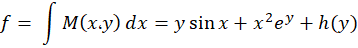
حال بایدh(y)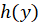 را بدست آوریم و برای این کار ازf
را بدست آوریم و برای این کار ازf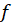 نسبت به متغیرy
نسبت به متغیرy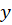 مشتق میگیریم:
مشتق میگیریم:
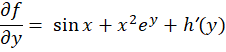
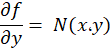
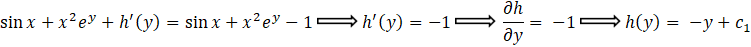
با توجه به اینکه فرم جواب عمومی این معادله برابر است باfx،y=c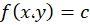 لذا داریم:
لذا داریم:
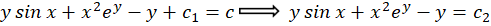
معادلات قابل تبدیل به معادله کامل

گاهی اوقات معادله کامل نیست ولی با ضرب تابعی مانند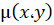 در طرفین معادله میتوان آن را به معادلهای کامل تبدیل نمود.در این صورت این تابع رافاکتور یاعامل انتگرال ساز مینامند.
در طرفین معادله میتوان آن را به معادلهای کامل تبدیل نمود.در این صورت این تابع رافاکتور یاعامل انتگرال ساز مینامند.
تمامی توابع دارای فاکتور انتگرال ساز نیستند و پیدا کردن این عامل در حالت کلی کار دشواری است ولی در ادامه به بررسی مواردی میپردازیم که میتوانند شما را در پیدا کردن این فاکتورها ( در صورت وجود ) یاری کنند.
به صورت کلی اگر در سوال بیان شد کهفاکتور انتگرال سازی به شکل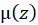 داریم که در آن
داریم که در آن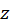 تابعی از
تابعی از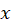 و
و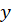 است آن گاه فاکتور انتگرال ساز برابر است با:
است آن گاه فاکتور انتگرال ساز برابر است با:
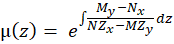
در غیر این صورت هر کدام از موارد زیر را بهدستآورید و در معادله چک کنید و اگرهر کدام از آنها باعث کامل شدن معادله شد همان فاکتور انتگرالساز است و از بررسی سایر موارد صرف نظر کنید و معادله را با توجه به روش حل معادلههای کامل حل کنید.
اگر هیچ کدام از موارد باعث کامل شدن معادله نشد پس باید معادله را به روشی غیر از حل معادلههای کامل حل کنید.حال به بیان این موارد میپردازیم:
1-اگر فاکتور انتگرالساز عبارتی صرفا بر حسبx باشد ، عامل انتگرالساز برابر است با :
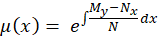
2- اگر فاکتور انتگرالساز عبارتی صرفا بر حسبy باشد ، عامل انتگرالساز برابر است با :
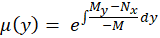
3- اگر فاکتور انتگرالساز عبارتی بر حسب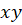 باشد ، عامل انتگرالساز برابر است با :
باشد ، عامل انتگرالساز برابر است با :
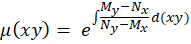
4- اگر فاکتور انتگرالساز عبارتی بر حسب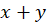 باشد ، عامل انتگرالساز برابر است با :
باشد ، عامل انتگرالساز برابر است با :
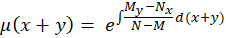
 مثال) معادله دیفرانسیل
مثال) معادله دیفرانسیل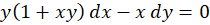 را حل کنید.
را حل کنید.
معادله فوق کامل نیست و سوال هم اشارهای به اینکه این معادله فاکتور انتگرالساز دارد یا خیر نکردهاست پس باید موراد چهارگانه را به ترتیب بررسی کنیم.با بررسی مورد اول و چککردن در معادله متوجه میشویم که فاکتور انتگرالساز نمیتواند عبارتی صرفا بر حسبx باشد.حال به بررسی مورد دوم میپردازیم.اگر فرض کنیمعامل انتگرالساز عبارتی تنها برحسبy است پس باید برابر باشد با:
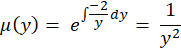
اکنون برای چک کردن این عامل ابتدا آن را در طرفین معادله ضرب میکنیم:
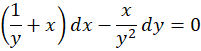
سپس شرط کامل بودن معادله را بررسی میکنیم:
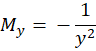
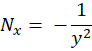
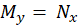
حال با یه معادله کامل روبرو هستیم که با روشهایی که پیش از این گفته شده به سادگی قابل حل است.
معادله دیفرانسیل خطی مرتبه اول
تعریف
فرم کلی این معادلات به یکی از دو صورت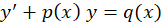 و
و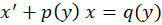 است که مورد اول خطی نسبت به
است که مورد اول خطی نسبت به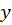 و مورد دوم خطی نسبت به
و مورد دوم خطی نسبت به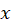 است.
است.
روش حل معادلات دیفرانسیل خطی مرتبه اول
اگرمعادله دیفرانسیل خطی نسبت به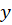 باشد جواب عمومی معادله برابر است با:
باشد جواب عمومی معادله برابر است با:
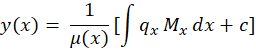
که در این معادله مقدار 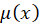 برابر است با:
برابر است با:
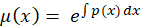
توجه کنید که اگر معادله ما خطی نسبت بهx بود هم جواب عمومی معادله برابر است با:
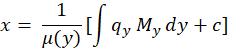
 مثال) معادله
مثال) معادله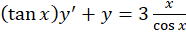 را حل کنید.
را حل کنید.
این معادله در نگاه اول یک معادله دیفرانسیل خطی مرتبه اول نیست پس طرفین معادله را در ضرب میکنیم و به معادله زیر میرسیم:
ضرب میکنیم و به معادله زیر میرسیم:
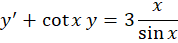
حال به معادله خطی مرتبه اولی رسیدیم که آن را به شکل زیر حل میکنیم:
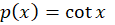
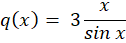
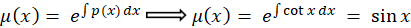
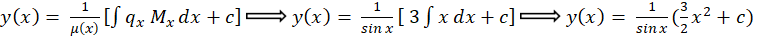
برای تسلط بیشتر بر این مباحث، میتوانید کپسول آموزشی معادلات دیفرانسیللینوم را مشاهده کنید.