معادله دیفرانسیل جداشدنی

در آموزش گذشته، بامعادله دیفرانسیل آشنا شدیم. در اینآموزش کپسولی لینوم، قصد داریم به سراغ یادگیری معادله دیفرانسیل جداشدنی و معادله دیفرانسیل همگن برویم.

تعریف

معادله دیفرانسیل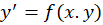 را جداشدنی یا تفکیک پذیر می‌نامیم هر گاه تابع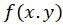تابعی جداشدنی باشد و این به معنای آن است که تابع 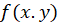را بتوان به صورت زیر نوشت:

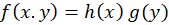
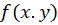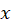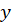یعنی بتوان تابع را به صورت حاصل ضرب تابعی بر حسب و نوشت.

مثال) تفکیک‌پذیری معادله دیفرانسیل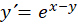 را بررسی کنید.

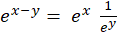
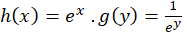
مثال) معادله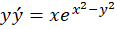 را حل کنید.

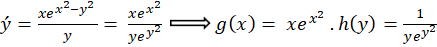
برای حل معادله باید یک سمت از تساوی را فقط بر حسب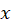 و سمت دیگر را فقط بر حسب 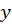بنویسید و سپس از طرفین انتگرال بگیرید:

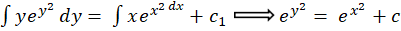
آموزش حل معادلات قابل تبدیل به معادلات جداشدنی

بعضی از معادلات در نگاه اول جداشدنی نیستند ولی می‌توان آن ها را بهمعادله جداشدنی تبدیل نمود و سپس به راحتی معادله مذکور را حل نمود.غالبا این نوع از معادلات به وسیله تغییر متغیر تفکیک‌پذیر خواهند‌شد.در مثال زیر روش حل این شکل از معادله را به خوبی یاد خواهید‌گرفت.

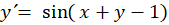مثال) معادله  را حل کنید.

معادله فوق جدا‌شدنی نیست ولی اگر قرار دهیم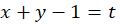 آن گاه داریم:

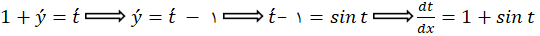
حال به معادله‌ای جداشدنی بر حسب دو متغیرx وt رسیدیم:

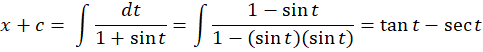
 به جای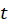  ،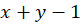 قرار می‌دهیم:

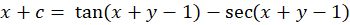
معادله دیفرانسیل همگن

تعریف

معادله دیفرانسیل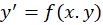 را همگن می‌نامند در صورتی که 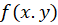تابعی همگن از درجه صفر باشد.

تابع همگن

تابع دو متغیره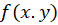 تابعی همگن است از درجه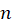(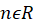) است هر گاه به ازای هر 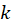(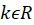) داشته‌باشیم:

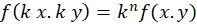
به طورمثال در مورد تابع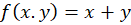 با توجه به معادله 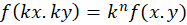به این نتیجه می‌رسیم که 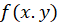تابعی همگن ار درجه یک می‌باشد.

آموزش حل معادله دیفرانسیل همگن

ابتدا باید بررسی شود کهمعادله همگن است یا خیر.در صورتی که معادله همگن بود می‌توانید معادله را با استفاده از تغییر متغیر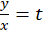 به راحتی حل کنید.

برای بررسی همگن بودن معادله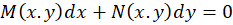 باید بررسی کنید که 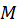و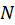 هر دو تابعی همگن با درجه یکسان باشند.

مثال) معادله همگن زیر را حل کنید.

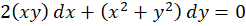
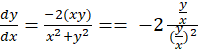
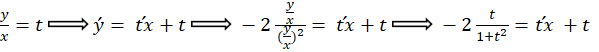
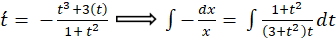
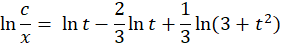
نهایتا به جای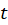 ، را قرار می‌دهیم و بدین صورت جواب معادله بدست می‌آید.

آموزش حل معادلات قابل تبدیل به معادلات همگن

برخی معادلات در نگاه اول همگن نیستند اما ممکن است تحت شرایطی بتوان آن‌ها را همگن کرد.گاهی اوقات با به کار‌گیری تغییر متغیر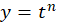 و در صورتی که بتوان 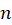ای را پیدا کرد که به ازای آن معادله همگن شود ، معادله به سادگی قابل حل می‌باشد.

مثال) معادله دیفرانسیل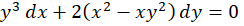  را حل کنید.

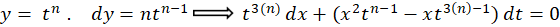
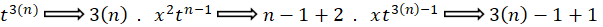
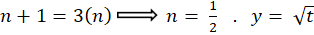
به ازای این مقدار از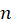 ، 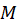و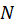 دارای درجه همگنی برابر بوده و معادله نیز تبدیل به معادله‌ای همگن از درجه می‌گردد و به این ترتیب با توجه به روش‌های حلمعادله همگن این معادله به سادگی قابل حل می‌باشد.

برای تسلط بیشتر بر این مباحث، می‌توانید  کپسول آموزشی معادلات دیفرانسیللینوم را  مشاهده کنید.