معادله دیفرانسیل

در اینآموزشی کپسولی لینوم، به سراغ یادگیریمعادلات دیفرانسیل می‌رویم.

تعریف

معادله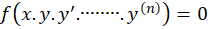 که از متغیر مستقل 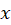، متغیر وابسته 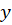و مشتقات 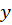تشکیل شده‌است رامعادله دیفرانسیل می‌نامیم و هدف از حل آن یافتن 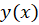است.

مرتبه معادله

تعریف

بالاترین مرتبه مشتق در معادله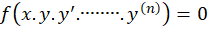 را مرتبه معادله دیفرانسیل می‌نامند.

درجه معادله دیفرانسیل

تعریف

اگر بتوان معادله دیفرانسیل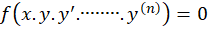 را به صورت یک چندجمله ای نسبت به متغیر وابسته 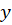و مشتقات آن نوشت، دراین صورت بالاترین درجه‌ی بالاترین مرتبه مشتق موجود در معادله را درجه معادلهدیفرانسیل می‌نامیم.

مثال) مرتبه و درجه دو معادله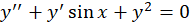  و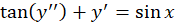را تعیین کنید.

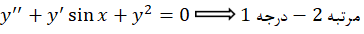
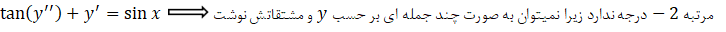
معادله دیفرانسیل خطی

تعریف

اگر معادله دیفرانسیل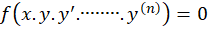 به صورت زیر باشد:

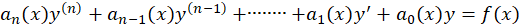
یعنی ضرایب معادله توابعی از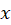 باشند ، معادله فوقمعادله دیفرانسیل خطی نامیده می‌شود.

پوش خانواده منحنی

تعریف

اگر یک خانواده منحنی را به شکل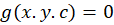 فرض کنیم ، آنگاه پوش این خانواده یک منحنی به فرم 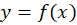است که بر تمام اعضای خانواده منحنی 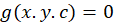و بر هر کدام تنها در یک نقطه مماس است. نکته ای که باید به آن توجه داشته‌باشید این است که معادله پوش یک خانواده منحنی در معادله خود آن خانواده منحنی صدق می‌کند.

روش بدست آوردن پوش یک خانواده منحنی

اگر خانواده منحنی را به صورت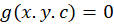 فرض کنیم آن گاه پوش آن از حذف 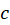از دستگاه زیر بدست خواهد‌آمد:

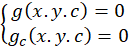
مثال) پوش خانواده منحنی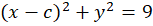 را بدست‌آورید.

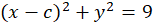
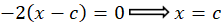
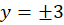
مسیر های هم زاویه

تعریف

اگر یک خانواده منحنی به شکل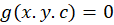 داشته‌باشیم مسیر هم‌زاویه با این خانواده منحنی مسیری است که تمام اعضای این خانواده را با زاویه‌ای معین قطع کند.

اگر یک خانواده منحنی به فرم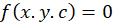 داشته‌باشیم که تمام اعضای آن ، همه‌ی اعضا خانواده منحنی 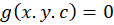را با یک زاویه مشخص قطع کند آنگاه  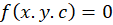را مسیر‌های هم زاویه با خانواده منحنی 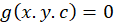می‌نامیم.

روش بدست‌آوردن مسیر‌های هم‌زاویه با یک خانواده منحنی

اگر یک خانواده منحنی به صورت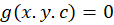 را فرض کنیم و قصد ما بدست‌آوردن خانواده منحنی به فرم 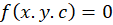باشد که مسیر‌های هم زاویه با 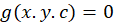با زاویه معین 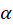را تشکیل می‌دهند به ترتیب زیر عمل می‌کنیم:

1-ابتدا معادله دیفرانسیل خانواده منحنی داده‌شده را بدست می‌آوریم.

2-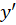 را از معادله دیفرانسیل فوق بدست می‌آوریم.

3-بعد از بدست‌آوردن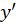 آن را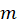 می‌نامیم و و نهایتا با حل معادله زیر مسیر‌های هم زاویه را بدست می‌آوریم:

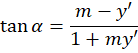
مثال) خانواده منحنی مسیر‌های هم‌زاویه با خانواده منحنی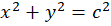 تحت زاویه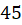درجه را مشخص کنید.

ابتدا از طرفین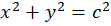 مشتق می‌گیریم:

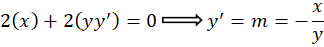
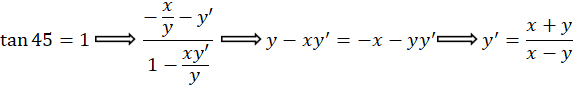
معادله همگن می‌باشد و با توجه به روش حل معادله همگن که پیش از این به تفضیل تشریح شد می‌توان این معادله را با تغییر متغیر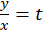 به سادگی حل نمود و نهایتا خانواده منحنی مسیر‌های هم زاویه با خانواده منحنی 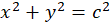تحت زاویه 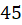درجه برابر است با:

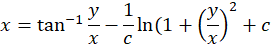
مسیرهای قائم

تعریف

هر گاه هر منحنی از خانواده منحنی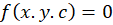 بر تمام منحنی‌های خانواده منحنی 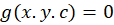عمود باشد، آنگاه خانواده منحنی 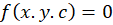را مسیرهای متعامد 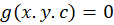می‌نامند.در واقع مسیرهای قائم همان مسیرهای هم‌زاویه تحت زاویه معین 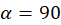 می‌باشند.

روش بدست‌آوردن مسیرهای قائم یک خانواده منحنی

1- ابتدامعادله دیفرانسیل خانواده منحنی داده شده را بدست می‌آوریم.

2-در این مرحله باید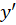 را با 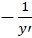جایگزین کنیم.

3-معادله حاصل را حل می‌کنیم و جواب این معادله میسرهای قائم بر خانواده محنی داده شده‌است.

مثال) مسیرهای قائم بر خانواده منحنی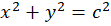 را بدست‌آورید.

ابتدا از طرفین 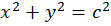 مشتق می‌گیریم:

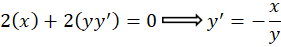
حال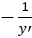را به جای 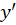قرار می‌دهیم:

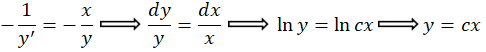
برای تسلط بیشتر بر این مباحث، می‌توانید  کپسول آموزشی معادلات دیفرانسیللینوم را  مشاهده کنید.