معادلات دیفرانسیل معروف
در اینآموزش معادلات دیفرانسیل لینوم، به سراغ یادگیریمعادلات دیفرانسیل معروف می‌رویم.
انواع معادلات با اشکال متفاوتی وجود دارند که می‌توان آن ها را با ترفندهایی به معادله خطی مرتبه اول تبدیل نموده و به راحتی حل کرد که در ادامه به بررسی آن ها می‌پردازیم:
معادله دیفرانسیل برنولی
تعریف
این دسته معادلات به صورت فرم‌های مختلفی وجود دارند ولی ما در این مقاله به بررسی یک مورد خاص از این دسته که به شکل زیر است می‌پردازیم:
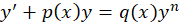
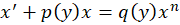
روش حل معادله دیفرانسیل برنولی
برای حل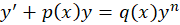 
ابتدا باید کاری کنیم تا در سمت راست معادله فقط عبارتی بر حسبx باقی بماند پس طرفین معادله را در
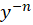ضرب می‌کنیم و معادله به شکل
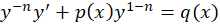در خواهد آمد.
بعد از رسیدن به این معادله باید از تغییر متغیر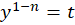
استفاده کنیم:
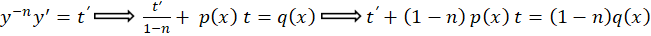
و به این ترتیب به یکمعادله خطی مرتبه اول میرسیم که روش حل آن در همین مطلب آمده است.طریقه حل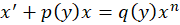
هم به همین شکل است.
مثال) معادله دیفرانسیل
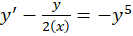را حل کنید.
ابتدا طرفین معادله را در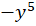
ضرب می‌کنیم:
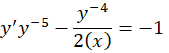
حال تغییر متغیر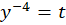
را انجام میدهیم و داریم:
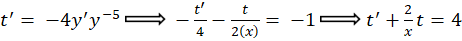
به یکمعادله دیفرانسیل خطی مرتبه اول رسیدیم بنابراین:
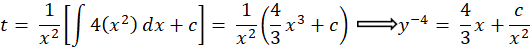
معادله دیفرانسیل ریکاتی
تعریف
معادلات دیفرانسیل ریکاتی معادلاتی به فرم کلی زیر هستند:
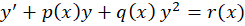
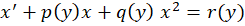
روش حل معادلات دیفرانسیل ریکاتی
برای حل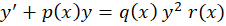 
حتما باید یک جواب معادله را بدانیم. اگر فرض کنیم معادله دارای جواب مشخص
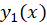باشد ( جواب خصوصی معادله ) در این صورت جواب عمومی معادله برابر است:
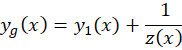
حال این جواب را در معادله صدق میدهیم تا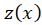 
به‌دست آید و جواب عمومی مشخص شود. برای اینکه سریع‌تر بتوانید مقدار
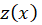را به‌دست آورید میتوانید مستقیما آن را در معادله زیر جایگذاری کنید:
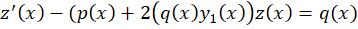
مثال) اگر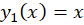
یکی از جواب‌های معادله
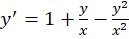باشد جواب عمومی این معادله را به‌دست آورید.
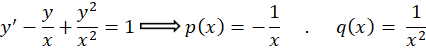
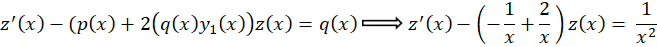
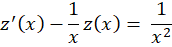
به معادله خطی مرتبه اول رسیدیم:
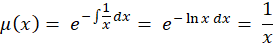
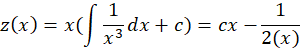
و نهایتا هم جایگذاری را انجام میدهیم:
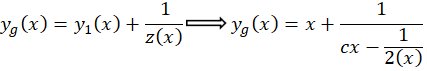
و به این ترتیب بررسی معادلات خاص قابل تبدیل بهمعادله خطی مرتبه اول به پایان رسید.
معادله کلرو
تعریف
فرم کلی این معادله به صورت زیر است:
روش حل معادله کلرو
برای حل این معادله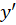
را برابر با 
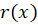قرار میدهیم (
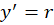) و سپس از طرفین نسبت به
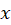معادله مشتق می‌گیریم و با استفاده از جایگذاری مجدد
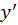با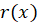
می‌توانیم به مقدار
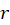برسیم و در نهایت
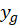را به‌دست آوریم.حتما در ادامه به مثال توجه نمایید تا بتوانید کاملا با روش حل معادله کلرو آشنا شوید.
مثال) جواب عمومی معادله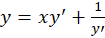 
را بدست آورید.
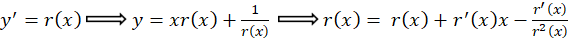
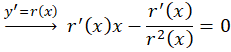
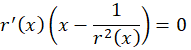
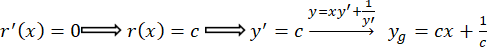
معادلات دیفرانسیل مرتبه اول منحصر به فرد
ما موارد مختلفی از معادلات و روش حل آن‌ها را بررسی کردیم ولی دسته ای از معادلات وجود دارند که شبیه هیچ کدام از گروه‌های قبلی نیستند و دارای روش حل متفاوتی هستند که در ادامه به بررسی آن‌ها می‌پردازیم:
1-اگر معادله به صورت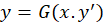 
بود ابتدا
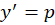قرار میدهیم سپس از طرفین معادله دیفرانسیل گرفته و با توجه به
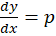به جای
،
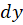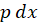قرار میدهیم.حالا به یک معادله دیفرانسیل مرتبه اول بر حسب
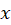و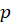
رسیدیم که جواب عمومی آن به صورت
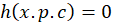است.
نهایتا با استفاده از دستگاه زیر و حذف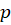
به جواب معادله میرسیم:
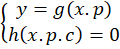
مثال) معادله دیفرانسیل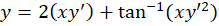
را حل کنید. ( 
)
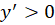ابتدا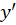
را برابر با
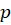قرار میدهیم:
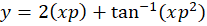
سپس از طرفین دیفرانسیل می‌گیریم و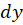
را برابر با 
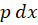قرار میدهیم:
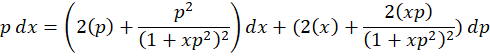
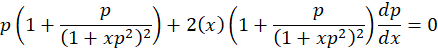
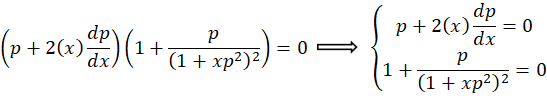
عبارت دوم به خاطر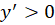
نمی‌تواند برقرار شود و باید مخالف صفر باشد پس داریم:
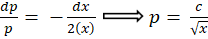
دستگاه را تشکیل میدهیم:
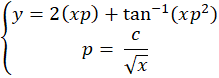
و با حذف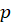
از طرفین داریم:
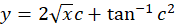
2- برای معادلاتی که به صورت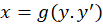
هستند نیز روشی کاملا مشابه حالت اول را طی می‌کنیم یعنی باید
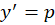قرار دهیم ، سپس از طرفین دیفرانسیل بگیریم و نهایتا با توجه به رابطه
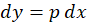به جای
،
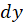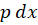قرار میدهیم.
3-اگربخواهیم معادله‌ای به صورت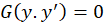
را حل کنیم با حالات مختلفی روبرو می‌شویم.
به طور مثالمعادله جدا شدنی و به راحتی قابل حل است یا اینکه به شکل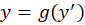
است و با توجه به روش
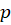می‌توان آن را حل نمود ولی گاها هیچ یک از دو حالت مذکور رخ نمی‌دهد. در چنین حالتی باید دو تابع به صورت
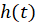و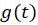
پیدا کنیم که در معادله صدق کنند یعنی
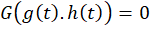و سپس به جای
،
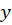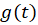و به جای
،
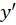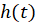قرار دهیم و معادله را حل کنیم.برای حل معادله 
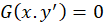نیز باید همین رویه را در پیش بگیرید.
مثال) معادله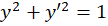
را حل کنید.
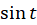و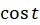
در معادله فوق صدق می‌کنند پس 
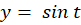و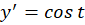
را قرار میدهیم:
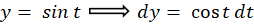
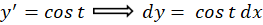
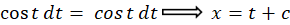
با توجه به دو عبارت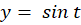
و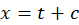
نتیجه می‌گیریم:
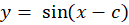
برای تسلط بیشتر بر این مباحث، میتوانید کپسول آموزشی معادلات دیفرانسیللینوم را مشاهده کنید.