1) معرفی اعداد مختلط و ویژگیهایاعداد مختلط
در اینآموزش کپسولی لینوم به سراغ یادگیریاعداد مختلط میرویم.
در حل معادله درجهدوم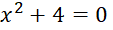 داریم :
داریم :
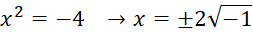
میبینید که در جوابهای این معادله درجهدوم عامل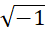 ظاهر میشود که در مجموعه اعدادحقیقی تعریف شدهاست اما به هرحال جزئی از جواب این معادله میباشد.
ظاهر میشود که در مجموعه اعدادحقیقی تعریف شدهاست اما به هرحال جزئی از جواب این معادله میباشد.
در تئوری اعدادمختلط دانشمندان عامل 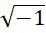 را به عنوان یک عدد موهومی محض پذیرفتند و با نماد
را به عنوان یک عدد موهومی محض پذیرفتند و با نماد 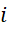 نشان دادند.
نشان دادند.
مجموعه اعدادمختلط ، که آن را با حرف C(Complex ) نمایش میدهیم، شامل کلیه اعدادی به شکل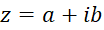 است که در آن
است که در آن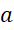 و
و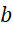 اعداد حقیقی بوده و
اعداد حقیقی بوده و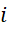 ، واحد مختلط، دارای خاصیت
، واحد مختلط، دارای خاصیت 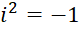 است.
است.
عدد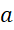 بخش حقیقی و عدد
بخش حقیقی و عدد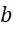 بخش موهومی نامیده میشوند و مینویسیم :
بخش موهومی نامیده میشوند و مینویسیم :

اگر 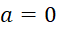 ، آنگاه عدد
، آنگاه عدد 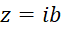 یک عدد موهومی محض و اگر
یک عدد موهومی محض و اگر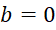 ، آنگاه عدد
، آنگاه عدد 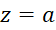 یک عدد حقیقی محض نامیده میشوند. مثلا عدد
یک عدد حقیقی محض نامیده میشوند. مثلا عدد 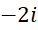 یک عدد موهومی محض و عدد-5 یک عدد حقیقی محض است.
یک عدد موهومی محض و عدد-5 یک عدد حقیقی محض است.
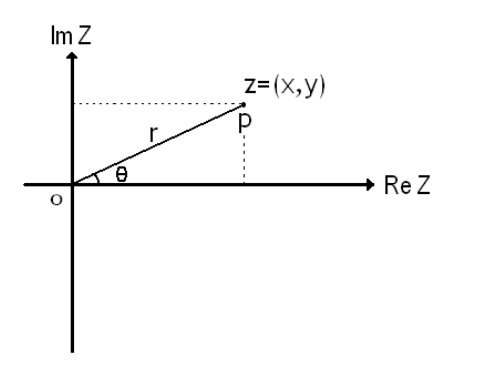
برای نمایش اعدادمختلط، ما از صفحه مختلط استفاده میکنیم. عدد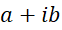 به صورت هندسی به عنوان نقطه ای به مختصات
به صورت هندسی به عنوان نقطه ای به مختصات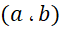 در صفحه دکارتی تعبیر میشود. محور
در صفحه دکارتی تعبیر میشود. محور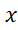 ها را محور حقیقی و محور
ها را محور حقیقی و محور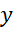 ها رامحور موهومی مینامند.
ها رامحور موهومی مینامند.
مبدا مختصات متناظر با عدد مختلط صفر است.

تساوی دو عدد مختلط
اگر 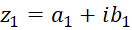 و
و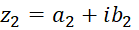 ، آنگاه شرط لازم و کافی برای تساوی
، آنگاه شرط لازم و کافی برای تساوی و
و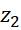 این است که داشتهباشیم
این است که داشتهباشیم 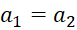 و
و 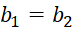 . از این نتیجه در حل معادلات شامل متغییرهای مختلط استفاده میشود. در حل این معادلات کافی است که بخشهای حقیقی و موهومی دو طرف تساوی را برابر یکدیگر قراردهیم تا جوابهای معادله نتیجه گردد.
. از این نتیجه در حل معادلات شامل متغییرهای مختلط استفاده میشود. در حل این معادلات کافی است که بخشهای حقیقی و موهومی دو طرف تساوی را برابر یکدیگر قراردهیم تا جوابهای معادله نتیجه گردد.
 مثال) معادله
مثال) معادله 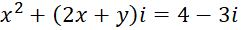 را حل کنید.
را حل کنید.
حل: با برابر قرار دادن بخشهای حقیقی و موهومی دوطرف معادله داریم:
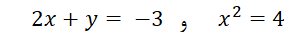
چون 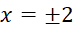 ، بنابراین جوابهای معادله برابر
، بنابراین جوابهای معادله برابر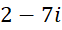 و
و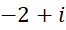 میباشند.
میباشند.
شکل قطبی اعدادمختلط
به دلیل طبیعت دوبعدیاعدادمختلط ، برای نمایش عددمختلط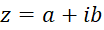 در صفحه میتوانیم از مختصات قطبی و استفاده کنیم، اگر
در صفحه میتوانیم از مختصات قطبی و استفاده کنیم، اگر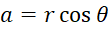 و
و 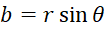 ، آنگاه برای
، آنگاه برای 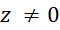 داریم :
داریم :
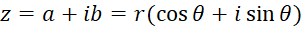
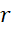 را قدرمطلق عددمختلط
را قدرمطلق عددمختلط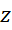 نامیده و داریم :
نامیده و داریم :
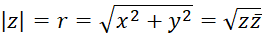
از نظر هندسی هم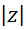 ، فاصله
، فاصله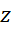 از مبدا مختصات میباشد. (بنابراین میتوان گفت
از مبدا مختصات میباشد. (بنابراین میتوان گفت 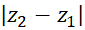 هم فاصله بین
هم فاصله بین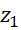 و
و است.)
است.)
در این تعریف 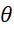 را آرگومان
را آرگومان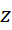 نامیده و با نماد
نامیده و با نماد 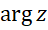 نمایش میدهیم و داریم :
نمایش میدهیم و داریم :
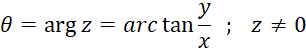
از نظر هندسی هم زاویه جهتدار بین جهت مثبت محور
زاویه جهتدار بین جهت مثبت محور  و
و  است. (شکل بالا)
است. (شکل بالا)
نکته:عدد مختلط رابه صورت
رابه صورت 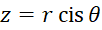 یا
یا 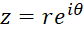 (فرم اویلری اعدادمختلط) نیز نشان میدهند.
(فرم اویلری اعدادمختلط) نیز نشان میدهند.
اعمال روی اعدادمختلط

اعمال جبری روی اعداد مختلط به صورت زیر تعریف میشوند :
1- حاصلجمع: 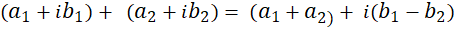
2- تفاضل: 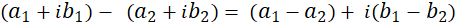
3- حاصلضرب: 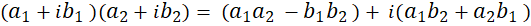
در اینجا از خاصیت 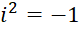 استفاده شدهاست.
استفاده شدهاست.
4- خارجقسمت:برای تقسیم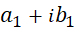 بر عدد غیرصفر
بر عدد غیرصفر 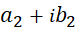 کافی است، صورت و مخرج را در
کافی است، صورت و مخرج را در 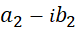 ضرب نماییم.
ضرب نماییم.
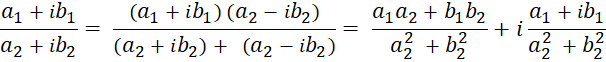
 مثال)اگر
مثال)اگر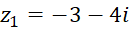 و
و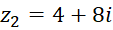 ، آنگاه :
، آنگاه :
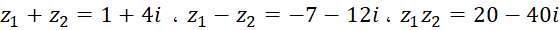
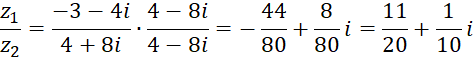
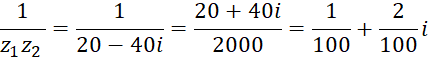
5- توان :اگر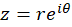 ، آنگاه به سادگی میتوان نشان داد که برای هر عدد طبیعی
، آنگاه به سادگی میتوان نشان داد که برای هر عدد طبیعی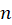 :
:
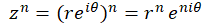
همچنین همواره داریم:
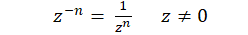
چون 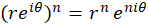 ، پس با فرض
، پس با فرض 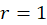 نتیجه میگیریم
نتیجه میگیریم 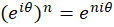 و یا به عبارتی دیگر :
و یا به عبارتی دیگر :

این اتحاد به فرمول دموآور معروف است.
 مثال) با استفاده از فرمول دموآور بسطهای
مثال) با استفاده از فرمول دموآور بسطهای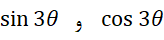 را بهدستآورید.
را بهدستآورید.
حل: کافی است در فرمول دموآور 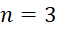 قرار دهیم ، پس :
قرار دهیم ، پس :
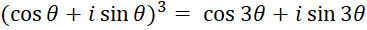
با توان رساندن عبارت سمت چپ و برابر قراردادن بخشهای حقیقی و موهومی نتیجه میگیریم :
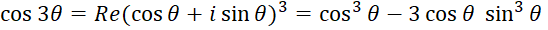
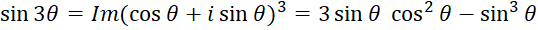
6- ریشه :برای تعیین ریشه ام یک عددمختلط غیرصفر ، ضروری است که ابتدا شکل قطبی به صورت
ام یک عددمختلط غیرصفر ، ضروری است که ابتدا شکل قطبی به صورت 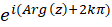 را تعیین کرده و سپس ریشه ها را از فرمول زیر محاسبه میکنیم :
را تعیین کرده و سپس ریشه ها را از فرمول زیر محاسبه میکنیم :
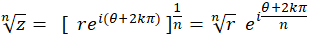
توجه کنید که برای مقادیر مختلف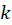 ، ریشههای مختلف نتیجه میگردند و چون برای
، ریشههای مختلف نتیجه میگردند و چون برای 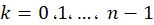 مجموعهای از n
مجموعهای از n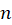 عدد متمایز حاصل میشوند که برای سایر مقادیر
عدد متمایز حاصل میشوند که برای سایر مقادیر 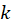 نیز همین مقادیر تکرار میگردند ، این مقدار متمایز
نیز همین مقادیر تکرار میگردند ، این مقدار متمایز 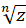 را ،
را ، 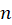 ریشه
ریشه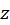 مینامند. ریشه متناظر با آرگومان اصلی (
مینامند. ریشه متناظر با آرگومان اصلی (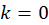 ) را ریشه اصلی میخوانند. این
) را ریشه اصلی میخوانند. این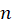 ریشه روی دایرهای به شعاع
ریشه روی دایرهای به شعاع 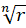 و به فواصل مساوی از یکدیگر واقع هستنند.
و به فواصل مساوی از یکدیگر واقع هستنند.
 مثال)ریشههای سوم عدد8 را بهدستآورید.
مثال)ریشههای سوم عدد8 را بهدستآورید.
حل: شکل قطبی عدد8 به صورت 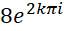 است. بنابراین ریشهها برابرند با :
است. بنابراین ریشهها برابرند با :
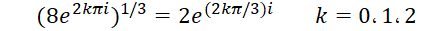
این ریشهها به ترتیب برابر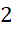 ،
، 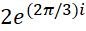 و
و 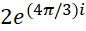 هستند. ریشه اصلی (برای
هستند. ریشه اصلی (برای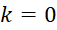 ) برابر
) برابر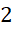 است. هر سه ریشه روی دایرهای به شعاع
است. هر سه ریشه روی دایرهای به شعاع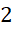 واقع بوده و اختلاف آرگومانهای آنها برابر
واقع بوده و اختلاف آرگومانهای آنها برابر است.
است.
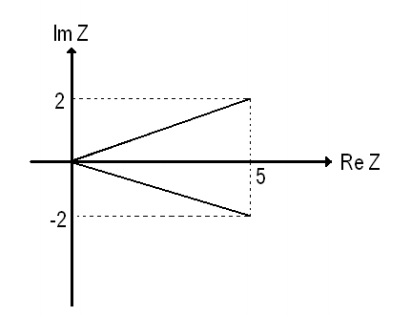
مزدوج یک عددمختلط
عدد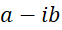 را مزدوج عدد
را مزدوج عدد 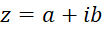 نامیده و آن را با
نامیده و آن را با 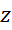 نمایش میدهیم. از نظر هندسی هم
نمایش میدهیم. از نظر هندسی هم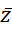 تصویر
تصویر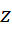 نسبت به محور حقیقی میباشد.
نسبت به محور حقیقی میباشد.
مثلا :
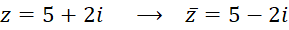
برای تسلط بیشتر بر این مباحث، میتوانید کپسول آموزش اعداد مختلط لینوم را هم مشاهده کنید.