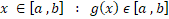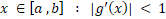توی این فصل فقط فقط روشهایی رو یاد می‌گیریم که میتونن معادله‌ی = 0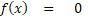 
رو حل بکنن...
خب شاید یک معادله‌ی جبری اینجوری نبود!!! چجوری به این شکل درش بیاریم؟؟؟
حواستون باشه! اول از همه باید یک بازه تعیین بکنیم و توی اون بازه دنبال ریشه بگردیم... شرطشم اینه که توی اون بازه فقط یک ریشه وجود داشته باشه و ریشه هم ریشه ساده باشه، نه مضاعف. پس این شرط‌ها رو باید داشته باشیم:
- تابع توی اون بازه پیوسته باشه.
- ضرب مقدار تابع در دو سر بازه منفی باشه.
- توی اون بازه مشتق هیچ جا صفر نشه.
هر کدوم از این شرط‌ها، خیالمون رو از بابت چی راحت میکنن؟؟؟
همه روشهایی که می‌گیم، یک سری روش‌های تکرار شونده هستن، یعنی با هر بار تکرار کردن یک سری عملیات به ریشه‌ی تابع نزدیک تر می‌شیم. پس یک جایی به این نتیجه می‌رسیم که به اندازه‌ی کافی به ریشه نزدیک شدیم و کار رو همون جا تمومش می‌کنیم. این که کی این‌کار رو بکنیم رو معیار توقف مشخص می‌کنه! کلا سه جور معیار توقف داریم:
- اینکه دقیقا چند بار تکرار کنیم!!!
- اینکه مقدار تابعمون از یک عدد مشخص به صفر نزدیک تر بشه.
- اینکه نسبت به مرحله قبلی چقدر به صفر نزدیک تر شدیم، اگر از یک حدی کمتر باشه، به تموم شدن عملیات رضایت می‌دیم!
خب، مقدمه‌ها تموم شدن، بریم سراغ اولین روش که بهش میگن روش تصنیف!!!
در این روش هی میاییم بازه‌مون رو نصف می‌کنیم... بعد می‌بینیم ریشه توی کدوم نصف از بازه هست... اون بازه ای که ریشه توش بود به عنوان بازه جدید در نظر می‌گیریم و همین کار رو اونقدر تکرار می‌کنیم تا یکی از معیارهای توقف اتفاق بیفته.
یک راه جدولی برای انجام این کار هست که خیلی خیلی ساده است و کامل توی ویدیوهای محاسبات عددی سایت توضیح داده شده.
فرض کنید معادله این باشه: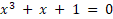 
، توی بازه صفر تا یک ریشه رو بدست بیارید... معیار توقف هم این باشه که مقدار تابع کمتر از یک‌صدم بشه!! محاسباتتون رو هم جوری انجام بدید که آخرش عدد رو تا 4 رقم اعشار بدست بیارید. (حواستون باشه بازه رو چک کنید و ببینید شرط‌هایی که گفته شده، برقراره واسش یا نه.
روش بعدی اسمش نابه‌جایی هست... هیچ فرقی با روش تنصیف نداره، فقط توی هر مرحله به جای وسط بازه،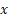
رو اینجوری در نظر می‌گیریم:
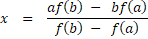
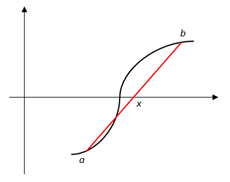
به کمک این نمودار پایین، میتونید توجیه کنید چرا همچین رابطه ای برای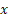 
در نظر گرفته شده؟؟؟
حالا رابطه به دست آوردن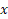
برای دو روش دیگه چیه؟؛ خودتون ببینید میفهمید چجوری به دست اومده این روابط؟؟ اگر هم ایده‌ای به ذهنتون نرسید، میتونید از ویدیو آموزشی استفاده بکنید...
برای روش نیوتون– رافسون داریم:
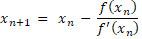
برای روش وتری هم می‌تونیم بنویسیم:
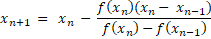
دو رابطه قبل یک تفاوت اساسی با روش‌های قبلی دارن!!! یک شباهت اساسی هم با هم دیگه دارن!!! میتونید این تفاوت و شباهت رو پیدا کنید؟؟ آیا میشه گفت روش وتری از روش نیوتون– رافسون به دست اومده؟؟؟
یک روش دیگه هم هست که اسمش تکرار ساده‌ست... واقعا هم تکراریه و هم ساده!!! ولی همگراییش تضمین شده نیست و باید دوتا شرط داشته باشه که بدونیم واقعا داریم به جواب نزدیکتر می‌شیم.
فرق بزرگی که این روش با روش‌های قبل داره اینه که اینجا کاری به ریشه معادله نداریم؛ به جاش معادله جبری رو به صورت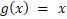 
در میاریم.
چجوری هر معادله‌ای رو به این شکل دربیاریم تا بتونیم از روش تکرار ساده استفاده کنیم؟؟
رابطه‌ای که در روش تکرار ساده استفاده می‌کنیم، به این صورت هست:
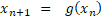
یعنی این که توی هر مرحله مقدار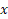
مرحله قبل رو می‌ذاریم توی تابع تا
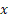مرحله بعدی به دست بیاد.
یادتون نره که معیار توقف رو توی هر مرحله چک کنید؛ ولی راستش رو بخواین توی این روش معیار توقف ممکنه یک ذره فرق بکنه!!! یعنی اونقدر جلو بریم تا عدد مرحله قبل، با عدد مرحله فعلی برابر بشه. ( با تعداد ارقام اعشار مشخص و محدود)
یادتونه گفتیم دو تا شرط اضافه هم برای همگرایی این روش نیاز داریم؟؟؟ الوعده وفا:
با استفاده از روش تکرار ساده، ریشه معادله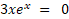 
رو به روش تکرار ساده، در بازه صفر تا یک و با در نظر گرفتن
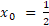به دست بیارید. محاسبات رو با سه رقم اعشار انجام بدید.
و ده‌ها نکته ناگفته دیگه که فقط توی مثال های خاص میشه دید... این مثال‌هارو میتونید توی ویدیوهای آموزشی ما ببینید.