مشتق تابع های مثلثاتی

 ابتدا با کاربرد مستقیم تعریف مشتق ازsin x مشتق می گیریم. سپس از قواعد مشتق گیری متداول و اتحادهای مثلثاتی استفاده می کنیم و مشتق های سایر توابع مثلثاتی را بدست می آوریم.

مشتق سینوس

بنابر تعریف مشتق می دانیم که مشتقy=sin x نسبت بهx عبارت است از حد

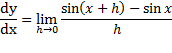
 برای محاسبه این حد، سه نتیجه از بحث های قبلی را به کار می بریم.

1.  

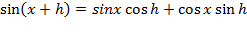
2.   

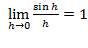
3.   

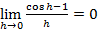
حال حدها را وقتیh→0 محاسبه می کنیم.

.

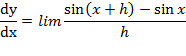
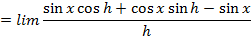
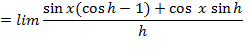
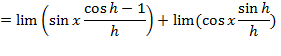
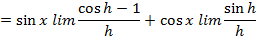
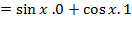
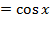
مشتقy=sin xنسبت بهx عبارت است از

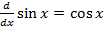
اگرu تابع مشتق پذیری ازx باشد، می توانیمقاعده زنجیری 

را در موردy=sin uبه کار ببریم و نتیجه بگیریم که 

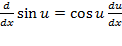
مثال

الف)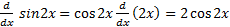 

ب)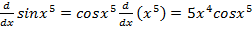    

پ)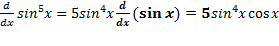     

پاسخ به پرسش(چرا در حساب دیفرانسیل و انتگرال از اندازه رادیانی استفاده می کنیم) در استدلال مربوط به این حکم نهفته است که مشتق سینوس، کسینوس است. این استدلال ایجاب می کند که :

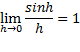
این حد 1 است تنها اگر اندازهh بر حسب رادیان باشد.

مثال : اگر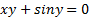  باشد،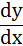 را با مشتق گیری ضمنی بیابید.

حل: از دو طرف معادله مشتق می گیریم وy را به عنوان تابع مشتق پذیری ازx تلقی می کنیم.

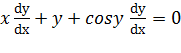
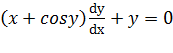
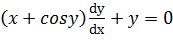
مشتق کسینوس

به منظور به دست آوردن فرمولی برای مشتقcosu از اتحادهای

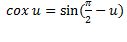
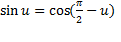
به صورت زیر استفاده می کنیم.

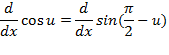
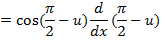
بنابراین:    

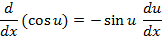
مشتق کسینوس تابعی مشتق پذیر برابر است با منهای سینوس تابع ضربدر مشتق تابع.

مثال:

الف)

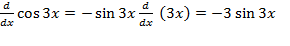
ب)

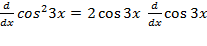
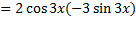
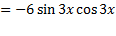
توجه: در مثال بالا قسمت (ب) پاسخ را می توان به صورت های دیگر نیز نوشت. مثلا می توانیم از اتحاد

و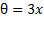 استفاده کنیم و پاسخ را به صورت زیر بنویسیم.

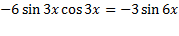
اگر در یک مساله مشتق گیری درمثلثات به جوابی برسید که با جواب شخص دیگری تفاوت داشته باشد ممکن است هر دو جواب درست باشد.

مشتق توابع مثلثاتی دیگر

چونsin x وcos x توابع مشتق پذیری ازx هستند، توابع

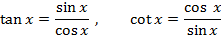
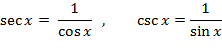
به ازای هر مقداری ازx  که تعریف بشوند، مشتق پذیرند. مشتق این توابع را می توان از قاعده خارج قسمت محاسبه کرد.

معادله های پارامتری

وقتی مسیر حرکت ذره متحرکی در صفحه نمودار یک تابع نباشد، نمی توانیم با بیان مستقیم y بر حسب x ، مسیر را توصیف کنیم. برای اجتناب از این مشکل، مختصات ذره را با دو معادله مانند معادلات زیر به صورت توابعی از یک متغیر سوم می نویسیم.

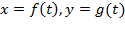
این نوع معادلات را معادلات پارامتریxوy، و متغیرt را پارامتر می نامند. پارامترt در بیشتر کاربردها زمان را نمایش می دهد، اما می تواند نمایشگر زاویه یا فاصله ای که ذره در امتداد مسیرش از آغاز می پیماید نیز باشد.

 مثال  معادلات

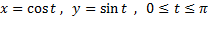
موضعp(x,y) ذره ای را که نیمه بالایی دایره واحد را ازA(1,0) تاB(-1,0) در خلاف جهت ساعت می پیماید نشان می دهند. ذره پس از نیم دور متوقف می شود.

فرمول پارامتری dy/dx

فرض کنید

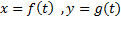
 توابع مشتق پذیری ازt باشند وdx/dt در بازه مربوط به مقادیرtهرگز صفر نشود. آنگاه به دلایلی می توان معادله

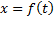
را، کهxرا به عنوان تابع مشتق پذیری ازtتعریف می کند، به صورتی در آورد کهt را به عنوان تابع مشتق پذیری ازx تعریف کند.

موقتا این تابع راt=h(x) می گیریم. چونt تابع مشتق پذیری ازx، وy تابع مشتق پذیری ازt است، ترکیبy=goh تابع مشتق پذیری ازx خواهد بود و به ازای هر مقدار خاصx ، داریمy=g(hx) .

مشتقات این توابع چه ارتباطی با هم دارند؟ بنابر قاعده زنجیری داریم

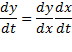
چونdx/dt≠0، دو طرف را برdx/dt تقسیم، وdy/dx را محاسبه می کنیم.

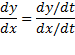
وقتی  x   وy به صورت پارامتری داده شده باشند، از این معادله برای محاسبهdy/dx استفاده می کنیم و برای این منظورdy/dt را برdx/dt تقسیم می کنیم.

خود به خودdy/dx را بر حسبt بیان می کند؛ لذا شیب مسیر حرکت هر ذره متحرک به ازای هر مقدارt را می توان یافت.

مثال  اگر

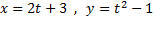
مطلوب است مقدارdy/dx درt=6 . همچنین،dy/dx را به عنوان تابعی ازx بیابید.

حل: معادله ای که در بالا بیان شد،dy/dx را به عنوان تابعی ازt به دست می دهد

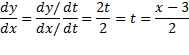
وقتیt=6 داریم

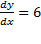
فرمول پارامتری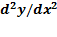

مشتق دومy نسبت بهx با دو مرتبه مشتق گرفتن ازy نسبت بهx به دست می آید:

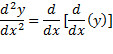
اگر معادلات پارامتری

 yرا به عنوان تابعی ازx تعریف کنند که دو مرتبه مشتق پذیر باشد، آنگاه می توانیم از معادله   

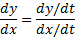
معادله

و از معادله زیر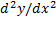  را محاسبه کنیم.

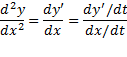
معادله اخیر حاکی است که برای محاسبه مشتق دوم 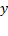  نسبت به  باید عملیات زیر را انجام دهیم.

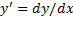1.    را بر حسبt به دست آوریم.

2. ازy' 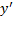 نسبت بهt مشتق بگیریم.

3. نتیجه را بر 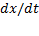 تقسیم کنیم.

مثال    اگر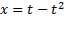  و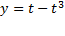  ،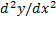  را بیابید.

حل:

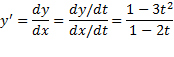
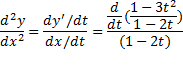
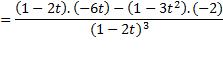
روش نیوتن برای تقریب زدن جواب معادله ها

وقتی فرمول دقیقی برای حل معادله ای چون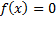  وجود ندارد، برای تقریب زدن جواب های مطلوب به روش های عددی روی می آوریم. یکی از روش ها، روش نیوتن، یا به زبان دقیق تر، روش نیوتن- رافسون نام دارد. این روش مبتنی بر این فکر است که در نزدیکی نقاطی کهf صفر شود، برای تقریب زدن نمودار 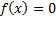 از خطوط مماس استفاده کنیم. باز هم می بینیم که خطی سازی کلید حل یک مساله علمی است.

دستورالعمل روش نیوتن

1. برای ریشه ای از معادله 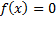، اولین تقریب راحد بزنید. نمودار 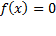می تواند به شما کمک کند.

2. از اولین تقریب برای به دست آوردن دومین، از دومین برای به دست آوردن سومین و غیره استفاده کنید. برای اینکه از تقریبn ام،x_n، تقریب بعدی،x_n+1، را بدست آورید از فرمول

که در آن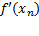 مشتق در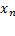 است استفاده کنید.

ابتدا نحوه اجرای این روش را نشان می  هیم و سپس به نظریه موید آن می پردازیم.

در مثال اول، تقریب های اعشاری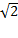 را با برآورد کردن ریشه مثبت معادله 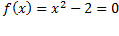به دست می آوریم.

مثال:  ریشه مثبت معادله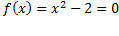 را بیابید.

حل: معادله

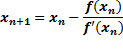
به ازای و ازای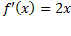 به صورت

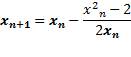
در می آید. برای  اینکه به طور موثر از ماشین حساب استفاده کنیم، معادله

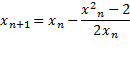
را به صورتی می نویسیم که عملیاتریاضی کمتری لازم باشد.

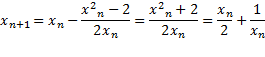
معادله

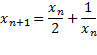
به ما این امکان را می دهد که با طی مراحل زیر از هر تقریب به تقریب بعدی برویم.

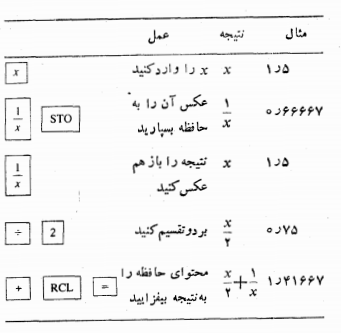
نتایجی که با مقدار آغازی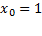 به دست می آید در ستون سمت چپ جدول زیر مشخص شده است. ( تا پنج رقم اعشار داریم )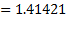

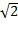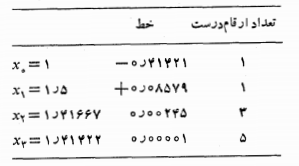
بیشتر ماشین حساب ها برای محاسبه ریشه، روش نیوتن را به کار می برند زیرا همگرایی بسیار سریعی دارد. اگر عملیات مذکور در جدول، به جای 5 رقم، تا 13 رقم اعشار انجام می شد آنگاه با با برداشتن گامی اضافه و رفتن به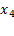، می توانستیم 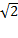را با بیش از 10 رقم اعشار به دست آوریم.

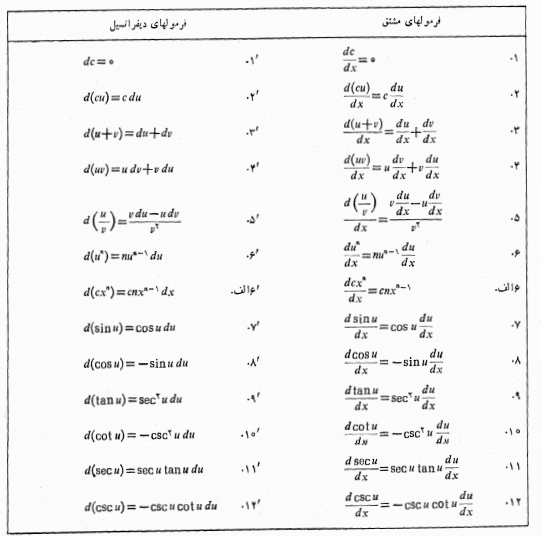
فرمول های مشتق با نماد دیفرانسیل

فرمول های مشتق به دست آمده با ضرب هریک درdx فرمول های نظیر دیفرانسیل به دست می آید. وقتی کهy تابع مشتق پذیری ازx باشد، برای یافتنdy می توانیم یا

الف-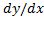 را بیابیم و نتیجه را در 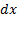ضرب کنیم یا

ب- یکی یا چند تا از فرمول های دیفرانسیل در جدول زیر را به کار گیریم.

نکته : اگر یک طرف معادله ای دیفرانسیل باشد، الزاما در طرف دیگر هم باید دیفرانسیل باشد.

مثال

الف)

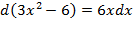
ب)

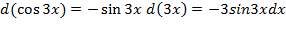
پ)

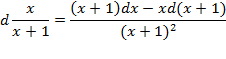
شایان توجه است که اگر در یک طرف معادله ای دیفرانسیل باشد، الزاما در طرف دیگر هم باید دیفرانسیل باشد. مثلا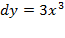 بی معنا است ولی 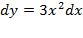معنا دارد.

کاربرد مشتق

رسم خط با استفاده از مشتق اول

وقتی بدانیم که تابعی در هر نقطه از بازه ایمشتق دارد، می دانیم که تابع در سراسر آن بازه پیوسته است، و نمودارش در آن بازه قطع شدگی ندارد. مثلا نمودارهای توابع مشتق پذیر و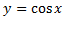، همانند نمودارهای چند جمله ای ها هر چه ادامه بیابند قطع نمی شوند. نمودارهای 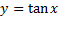و صرفا در نقاطی که توابع مربوط تعریف نمی شوند قطع می شوند. بر هر بازه ای که این نقاط را شامل نباشد، توابع مزبور مشتق پذیرند؛ و بنابراین پیوسته اند و نمودارهایشان قطع شدگی ندارند.

اگر بدانیم که مشتق تابعی کجا مثبت، کجا منفی یا کجا صفر است، آنگاره می توانیم درباره شکل نمودار آن تابع اطلاعاتی به دست آوریم. نمودار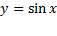   بر دامنه اش بینهایت بار بالاو پایین می رود. جایی که مشتق 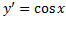 مثبت است بالا می رود، و جایی که منفی است پایین می آید.  در نقاط تحول بین بالارفتن و پایین آمدن، 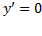  و مماس ها افقی هستند.

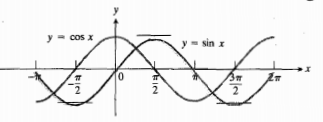
نمودار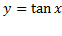  بینهایت تکه مجزا مرسوم به شاخه دارد. در هر شاخه 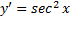  مثبت است و 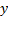تابعی است صعودی از .

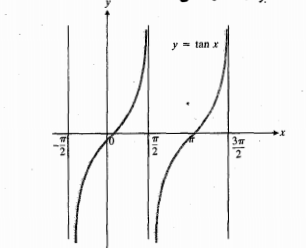
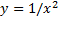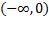نمودار   بر که در آنجا 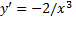مثبت است، صعودی است، و بر 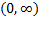که در آنجا

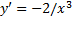  منفی است  نزولی است.

نمودار تابع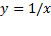 وقتی در محدوده بازه های 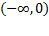 و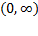 از چپ به راست حرکت می کند پایین می آید. مشتق 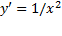  در سراسر هریک از این بازه ها منفی است، اما در 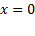تعریف نمی شوند.

آزمون مشتق اول برای توابع صعودی و نزولی

فرض کنید که یک تابعf در هر نقطه چونx از یک بازه مشتق داشته باشد. آنگاه

 f بر  صعودی است، هرگاه به ازای هرx در  , f'(x)>0

f بر نزولی است، هرگاه به ازای هرx در ,   f'(x)<0

آزمون مشتق اول به زبان هندسی حاکی است که توابع مشتق پذیر بر بازه هایی صعود می کنند که نمودارشان شیب مثبت داشته باشند، و بر بازه هایی نزول می کنند که نمودارشان شیب منفی داشته باشند.

مما س های افقی

از آنجا که مشتقی چونf' در هر بازه ی یی کهf' تعریف شود دارای ویژگی های مقدار میانی است، هر وقتf' در این بازه تغییر علامتمی دهد، باید مقدارش صفر شود. پس هر وقتf' در بازه تغییر علامت می دهد، نمودارf باید مماس افقی داشته باشد.

اگر وقتیx از چپ به راست می رود و از نقطه ای چونc می گذرد، مقدارf' از مثبت به منفی تبدیل شود، آنگاه مقدارf در یکc یک مقدار ماکسیمم موضعیf است. یعنیf(c) بزرگترین مقداری است که تابع در یک همسایگی نزدیک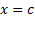 دارد.

اگر وقتیx از چپ به راست می رود و از نقطه ای چونd می گذرد، مقدار  f' از منفی به مثبت تبدیل شود، آنگاه مقدارf در  d یک مقدار مینیمم موضعی f است. یعنی 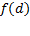  کوچکترین مقداری است که تابع در یک همسایگی نزدیک 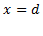 دارد.

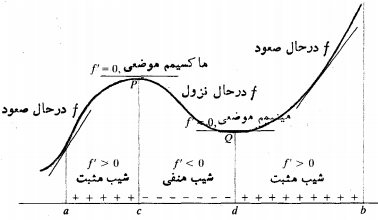
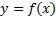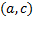تابع بر که در آنجا  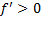، صعود می کند، بر 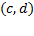که در آنجا 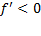 نزول می کند، و مجددا بر 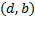صعود می کند. نقاط تحول با مماس های افقی مشخص شده اند.

رسم نمودار

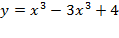مثال  نمودار تابع را رسم کنید.

حل : طبق شکل زیر. ابتدا طول ها و عرض های از مبدا (مختص های 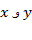 نقاط تقاطع یا تماس نمودار با محورها) را می یابیم. عرض از مبدا با قرار دادن به دست می آید.

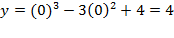
تجزیه چند جمله ای به صورت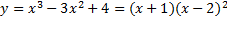                                               

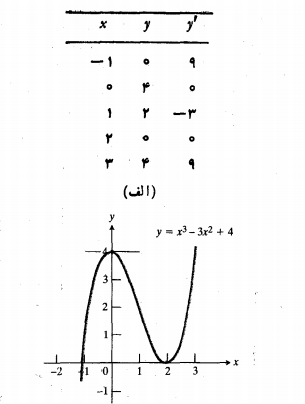
نشان می دهد که طول های از مبدا عبارت ان از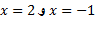 . حال می بینیم که مشتق تابع کجا مثبت، کجا منفی و کجا صفر است. مشتق عبارت است از 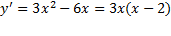 که در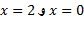 صفر است. به ازای این مقادیر خم مماس افقی دارد.

مشتق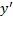 در طرف چپ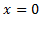که و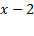 هر دو منفی اند، مثبت است، و در طرف راست 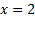که و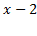 هر دو مثبت اند، نیز مثبت است. بنابراین، این تابع بر بازه های-∞,0)) و (2,∞) صعود می کنند.

بینx=2وx=0، مشتقy'=3x(x-2)  منفی است. زیرا3x>0 ولیx-2<0 . پس تابع بر بازه(0,2)نزول می کند.

جهت بهره مندی از مطالب بیشترسایت لینوم در مورد مبحث مذکور توصیه می کنیم ازاین  محصول استفاده کنید.