کاربرد مشتق
وجود مماس افقی بدون وجود ماکسیمم یا مینیمم
نمی توان گفت که هر وقتمشتق صفر شود، الزاما تغییر علامت انجام می شود.
مشتق تابع 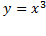 یعنی
یعنی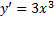 در مبدا صفر، و در دو طرف آن مثبت است. نمودار
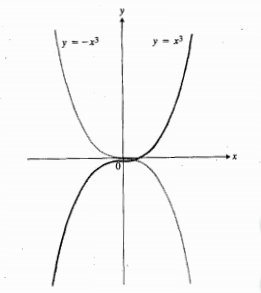
در مبدا صفر، و در دو طرف آن مثبت است. نمودار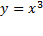 مماس در x=0 را قطع می کند، و به صعود خود ادامه می دهد. به همین ترتیب نمودار
مماس در x=0 را قطع می کند، و به صعود خود ادامه می دهد. به همین ترتیب نمودار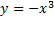 مماس افقی در x=0 را قطع می کند وبه نزول خود ادامه می دهد. مانند شکل زیر
مماس افقی در x=0 را قطع می کند وبه نزول خود ادامه می دهد. مانند شکل زیر
وجود ماکسیمم یا مینیمم در غیاب مماس افقی مماس
دیدیم یک تابع ممکن است در نقطه ای که
ممکن است در نقطه ای که 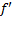 صفر است، یک مقدار ماکسیمم ی مینیمم موضعی داشته باشد. در عمل، این واقعه چنان به وفور رخ می دهد که جستجو برای یافتن صفرهای
صفر است، یک مقدار ماکسیمم ی مینیمم موضعی داشته باشد. در عمل، این واقعه چنان به وفور رخ می دهد که جستجو برای یافتن صفرهای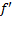 را ارزشمند می سازد.
را ارزشمند می سازد.

باید متوجه باشیم که ممکن است تابعی در نقطه ای که مشتق ندارد، مقدار ماکسیمم یا مینیمم موضعی داشته باشد. پس، جستجو برای یافتن مقادیر اکسترمم باید از حل معادله 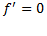 فراتر رود.
فراتر رود.
 مثال: تابع
مثال: تابع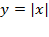 در
در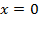 که
که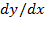 وجود ندارد مانند شکل زیر مقدار مینیمم خودش را به دست می آورد.
وجود ندارد مانند شکل زیر مقدار مینیمم خودش را به دست می آورد.
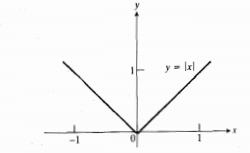
تقعر و نقطه عطف
همانطور که در شکل زیر دیده می شود تابع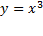 همراه با افزایش x ، صعود می کند؛ اما قسمتی ازخم که مربوط به بازه
همراه با افزایش x ، صعود می کند؛ اما قسمتی ازخم که مربوط به بازه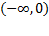 است و قسمت مربوط به
است و قسمت مربوط به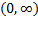 در جهت های متفاوتی می پیچند. اگر در امتداد خم از سمت چپ به طرف مبدا برویم، پیچش خم به سمت راست است. وقتی از مبدا دور می شویم، خم به سمت چپ می پیچد. قسمت چپ «به پایین خم می شود»، و قسمت راست«به بالا خم می شود».
در جهت های متفاوتی می پیچند. اگر در امتداد خم از سمت چپ به طرف مبدا برویم، پیچش خم به سمت راست است. وقتی از مبدا دور می شویم، خم به سمت چپ می پیچد. قسمت چپ «به پایین خم می شود»، و قسمت راست«به بالا خم می شود».
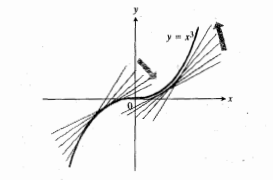
توصیف پیچش به طریق دیگر این است که وقتی نقطه تماس از سمت چپ به مبدا میل می کند، مماس بر خم در جهت ساعت می چرخد. در این حالت شیب خم تقلیل می یابد. وقتی نقطه تماس از مبدا وارد ربع اول می شود، ماس در خلاف جهت ساعت می چرخد. در این حالت شیب خم زیاد می شود.
تقعر خم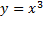 بر بازه ی
بر بازه ی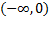 که در آنy' کم می شود رو به پایین است، و بر بازه ی
که در آنy' کم می شود رو به پایین است، و بر بازه ی 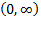 که در آن y' زیاد می شود رو به بالا است.
که در آن y' زیاد می شود رو به بالا است.
تعریف تقعر رو به پایین و تقعر برو به بالا
نمودار تابع مشتق پذیر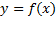 در بازه ای که y' کم می شود تقعر رو به پایین دارد، و در بازه ای که y' زیاد می شود تقعر رو به بالا دارد.
در بازه ای که y' کم می شود تقعر رو به پایین دارد، و در بازه ای که y' زیاد می شود تقعر رو به بالا دارد.
اگر تابع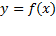 علاوه بر مشتق اول، مشتق دوم هم داشته باشد می توانیم آزمون مشتق اول را در مورد تابع
علاوه بر مشتق اول، مشتق دوم هم داشته باشد می توانیم آزمون مشتق اول را در مورد تابع
'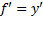 به کار ببریم و نتیجه بگیریم که اگر
به کار ببریم و نتیجه بگیریم که اگر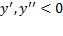 تقلیل می یابد، و اگر
تقلیل می یابد، و اگر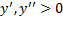 زیاد می شود. بنابراین، آزمونی داریم که می توانیم آن را در مورد فرمول
زیاد می شود. بنابراین، آزمونی داریم که می توانیم آن را در مورد فرمول 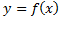 به کار ببریم و تقعر نمودارش را تعیین کنیم. نام این آزمون،آزمون مشتق دومبرای تقعر است.
به کار ببریم و تقعر نمودارش را تعیین کنیم. نام این آزمون،آزمون مشتق دومبرای تقعر است.
آزمون مشتق دوم برای تقعر
نمودار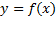 در بازه ای
در بازه ای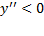 ، تقعر رو به پایین دارد و در بازه ای
، تقعر رو به پایین دارد و در بازه ای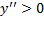 ، تقعر رو به بالا دارد.
، تقعر رو به بالا دارد.
مفهوم این آزمون این است که اگر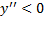 ، آنگاه با افزایش x , 'y کاهش می یابد و مماس در جهت ساعت می چرخد. بر عکس، اگر
، آنگاه با افزایش x , 'y کاهش می یابد و مماس در جهت ساعت می چرخد. بر عکس، اگر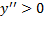 ، آنگاه x زیاد می شود،'
، آنگاه x زیاد می شود،'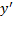 افزایش می یابد و مماس در خلاف جهت ساعت می چرخد.
افزایش می یابد و مماس در خلاف جهت ساعت می چرخد.
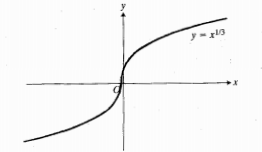
 مثال : طبق شکل زیر ، سراسر محور x ، خم
مثال : طبق شکل زیر ، سراسر محور x ، خم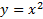 تقعر رو به بالا دارد زیرا
تقعر رو به بالا دارد زیرا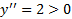 .
.
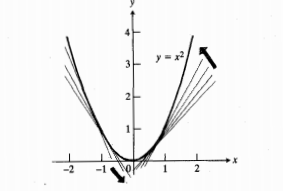
نقاط عطف
نقطه ای از خم که در آن تقعر عوض شود نقطه عطف نام دارد. پس نقطه عطف خمی که دوبار مشتق پذیر است نقطه ای است که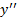 در یک طرفش مثبت و در طرف دیگرش منفی است. در نقطه عطف
در یک طرفش مثبت و در طرف دیگرش منفی است. در نقطه عطف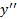 صفر است زیرا مشتق ها دارای ویژگی مقدار میانی هستند.
صفر است زیرا مشتق ها دارای ویژگی مقدار میانی هستند.

ممکن است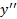 در نقطه ای که نقطه عطف نیست صفر باشد، و باید به این نکته توجه داشت مانند مثال زیر.
در نقطه ای که نقطه عطف نیست صفر باشد، و باید به این نکته توجه داشت مانند مثال زیر.
 مثال: بر اساس شکل زیر خم
مثال: بر اساس شکل زیر خم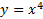 در
در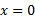 نقطه عطف ندارد. هر چند در آنجا
نقطه عطف ندارد. هر چند در آنجا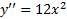 صفرمی شود. مشتق دوم در
صفرمی شود. مشتق دوم در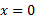 تغییر علامت نمی دهد ( در واقع هرگز
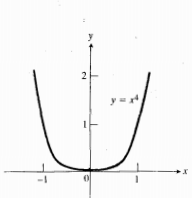
تغییر علامت نمی دهد ( در واقع هرگز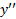 منفی نمی شود). خم در تمام محور
منفی نمی شود). خم در تمام محور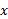 تقعر رو به بالا دارد زیرا را بر
تقعر رو به بالا دارد زیرا را بر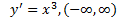 یک تابع صعودی است.
یک تابع صعودی است.
در این مثال می بینیم که گرچه شرط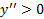 در آزمون مشتق دوم برای تقعر شرط کافی است، اما شرط لازم نیست. خم
در آزمون مشتق دوم برای تقعر شرط کافی است، اما شرط لازم نیست. خم 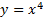 در مبدا تقعر رو به بالا دارد، اما
در مبدا تقعر رو به بالا دارد، اما 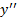 در مبدا مثبت نیست.
در مبدا مثبت نیست.
همچنین ممکن است نقطه عطف در جایی قرار بگیرد که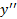 وجود نداشته باشد. در این زمینه به مثال زیر توجه کنید.
وجود نداشته باشد. در این زمینه به مثال زیر توجه کنید.
 مثال: در شکل زیر خم
مثال: در شکل زیر خم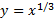 در
در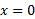 با اینکهمشتق دوم وجود ندارد، نقطه عطف دارد. برای ملاحظه این نکته
با اینکهمشتق دوم وجود ندارد، نقطه عطف دارد. برای ملاحظه این نکته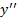 را به ازای
را به ازای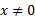 محاسبه می کنیم.
محاسبه می کنیم.
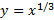
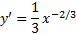

وقتی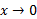 ،
،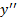 بینهایتمی شود. با وجود این به ازای
بینهایتمی شود. با وجود این به ازای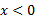 ، خم تقعر رو به بالا دارد ( در اینجا
، خم تقعر رو به بالا دارد ( در اینجا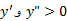 صعودی است) و برای
صعودی است) و برای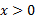 ( که در آن
( که در آن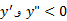 نزولی است ) تقعر رو به پایین دارد.
نزولی است ) تقعر رو به پایین دارد.
کاربرد رسم در نمودار
حال آنچه را آموخته ایم به کار می گیریم و نمودار یک چند جمله ای درجه سه را رسم می کنیم. مراحل 1 تا 5 که در حل مثال زیر آمده است دستورالعملی برای رسم نمودار است.
 مثال: خم زیر را رسم کنید.
مثال: خم زیر را رسم کنید.
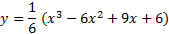
حل:
1.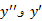 را محاسبه می کنیم.
را محاسبه می کنیم.
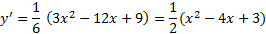
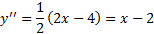
2.نقاطی را که در آن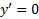 می یابیم و تعیین می کنیم که
می یابیم و تعیین می کنیم که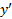 کجا مثبت است و کجا منفی . به این وسیله می توان دریافت که خم در کجا صعود می کند و در کجا نزول. نقاطی که در آن ها
کجا مثبت است و کجا منفی . به این وسیله می توان دریافت که خم در کجا صعود می کند و در کجا نزول. نقاطی که در آن ها 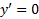 ممکن است مقادیر ماکسیمم و مینیمم موضعی را به دست دهند.
ممکن است مقادیر ماکسیمم و مینیمم موضعی را به دست دهند.
پس از تجزیه 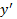 داریم:
داریم: 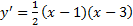
پس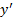 به ازای
به ازای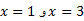 صفر است. طبق شکل زیر
صفر است. طبق شکل زیر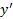 وقتی
وقتی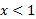 مثبت است،
مثبت است،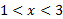 ، منفی است، و وقتی
، منفی است، و وقتی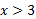 ، مجددا مثبت است. خم در
، مجددا مثبت است. خم در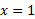 ( که در آن
( که در آن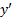 از + به – تغییر می کند) یک ماکسیمم موضعی، و در
از + به – تغییر می کند) یک ماکسیمم موضعی، و در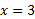
( که در آن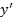 از –به + تغییر می کند) یک مینیمم موضعی دارد.
از –به + تغییر می کند) یک مینیمم موضعی دارد.
3.حال ببینیم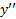 کجا صفر است، و نیز جاهایی را که
کجا صفر است، و نیز جاهایی را که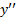 مثبت یا منفی است تعیین کنیم. از این راه اطلاعاتی در مورد تقعر به دست می آوریم. نقاطی که در آن ها
مثبت یا منفی است تعیین کنیم. از این راه اطلاعاتی در مورد تقعر به دست می آوریم. نقاطی که در آن ها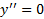 ، ممکن است نقاط عطف باشند.
، ممکن است نقاط عطف باشند.
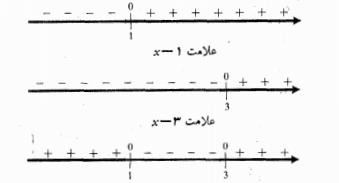
داریم :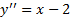
پس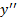 به ازای
به ازای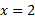 صفر ، به ازای
صفر ، به ازای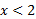 منفی، و به ازای
منفی، و به ازای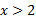 مثبت است. خم بر
مثبت است. خم بر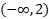 تقعر رو به پایین دارد و بر
تقعر رو به پایین دارد و بر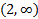 تقعر رو به بالا. نقطه
تقعر رو به بالا. نقطه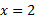 نقطه عطف است زیرا
نقطه عطف است زیرا 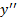 در
در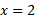 تغییر علامت می دهد.
تغییر علامت می دهد.
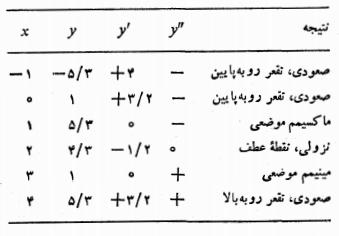
4.جدول کوچکی از مقادیر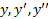 تشکیل می دهیم. این جدول اطلاعاتی را که تا به حال به دست آورده ایم را در بر دارد. عرض از مبدا، و مقادیر
تشکیل می دهیم. این جدول اطلاعاتی را که تا به حال به دست آورده ایم را در بر دارد. عرض از مبدا، و مقادیر چند نقطه اضافی را هم یادداشت می کنیم تا احساسی کلی از شکل خم به دست آوریم.
چند نقطه اضافی را هم یادداشت می کنیم تا احساسی کلی از شکل خم به دست آوریم.
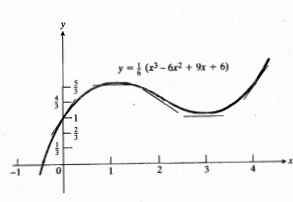
5.نقاط موجود در جدول را مشخص می کنیم، مماس ها را می کشیم، و از اطلاعات موجود درباره صعود، نزول و تقعر استفاده می کنیم و نمودار را رسم می کنیم.
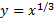
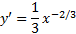
مجانب ها و تقارن
در این قسمت توابع گویا از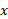 را با در نظر گرفتن رفتارشان، وقتی مخرج به صفر نزدیک یا
را با در نظر گرفتن رفتارشان، وقتی مخرج به صفر نزدیک یا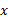 از لحاظ عددی بزرگ می شود، رسم می کنیم. نمودار تابع های فرد یا زوج تقارن هایی دارند که آگاهی از آن ها مهم است، بنابراین این مطلب را بررسی می کنیم.
از لحاظ عددی بزرگ می شود، رسم می کنیم. نمودار تابع های فرد یا زوج تقارن هایی دارند که آگاهی از آن ها مهم است، بنابراین این مطلب را بررسی می کنیم.

تقارن در نمودار تابع های زوج و فرد
تابع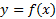 یک تابع زوج از
یک تابع زوج از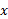 است هرگاه به ازای هر
است هرگاه به ازای هر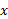 در دامنه تابع،
در دامنه تابع،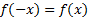 ؛ و یک تابع فرد است هرگاه به ازای هر
؛ و یک تابع فرد است هرگاه به ازای هر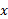 در دامنه تابع،
در دامنه تابع،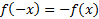 .
.
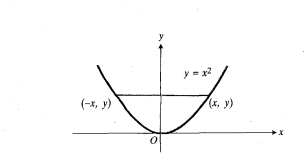
زوج بودن تابع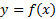 معادل است با اینکه نمودارش نسبت به محور
معادل است با اینکه نمودارش نسبت به محور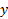 متقارن باشد. چون
متقارن باشد. چون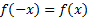 ، نقطه
، نقطه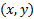 بر خم واقع است اگر و تنها اگر نقطه
بر خم واقع است اگر و تنها اگر نقطه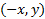 هم بر خم واقع باشد.
هم بر خم واقع باشد.
فرد بودن تابع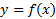 معادل است با اینکه نمودارش نسبت به مبدا متقارن باشد. چون
معادل است با اینکه نمودارش نسبت به مبدا متقارن باشد. چون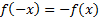 ، نقطه(x,y) بر خم واقع است اگر و تنها اگر نقطه
، نقطه(x,y) بر خم واقع است اگر و تنها اگر نقطه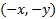 نیز بر خم واقع باشد.
نیز بر خم واقع باشد.
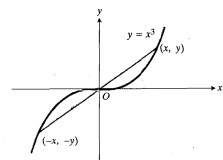
نمودارهای معادلاتی که صرفا شامل توان های زوجx باشند نسبت به محورy متقارن اند. اما قاعده متناظری برای توان های فرد و تقارن نسبت به مبدا وجود ندارد.
مثال: توابع
y=1+1x وy=1x-1
فرد نیستند، هر چند فرمول های آن ها تنها توان های فردx را شامل می شوند. در مورد اول
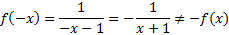
در مورد دوم
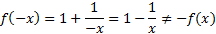
هیچ یک از نمودارها نسبت به مبدا متقارن نیست.
مجانب های افقی و قائم
وقتی یک نقطهp روی نمودار تابعی چون 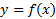 رفته رفته از مبدا دور می شود، ممکن است فاصله بینp و خطی ثابت به صفر نزدیک شود؛ به عبارت دیگر خم وقتی از مبدا دور می شود، به خط «میل می کند». در این حالت خط را مجانب نمودار می نامند. مثلا محورx و محورy ، مجانب های خم هایy=1/x2 وy=1/x هستند.
رفته رفته از مبدا دور می شود، ممکن است فاصله بینp و خطی ثابت به صفر نزدیک شود؛ به عبارت دیگر خم وقتی از مبدا دور می شود، به خط «میل می کند». در این حالت خط را مجانب نمودار می نامند. مثلا محورx و محورy ، مجانب های خم هایy=1/x2 وy=1/x هستند.
مثال مجانب های 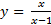 عبارت اند از خط هایy= 1 وx= 1 . این مطلب با تقسیمx برx- 1
عبارت اند از خط هایy= 1 وx= 1 . این مطلب با تقسیمx برx- 1
و سپس نوشتن معادله به صورت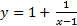 فورا آشکار می شود. خط
فورا آشکار می شود. خط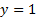 از سمت راست مجانب است زیرا
از سمت راست مجانب است زیرا
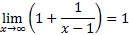
این خط از سمت چپ نیز مجانب است زیرا وقتی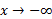 ،
،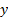 باز هم به 1 میل می کند. به ازای مقادیر بزرگ
باز هم به 1 میل می کند. به ازای مقادیر بزرگ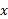 رفتار
رفتار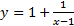 نظیر رفتار
نظیر رفتار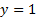 است. خط
است. خط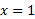 مجانب قائم شاخه سمت راست نمودار است زیرا
مجانب قائم شاخه سمت راست نمودار است زیرا
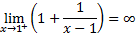
و مجانب قائم شاخه سمت چپ هم هست زیرا
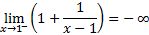
به ازای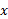 های نزدیک 1 رفتار این تابع شبیه رفتار
های نزدیک 1 رفتار این تابع شبیه رفتار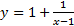 است. بطور کلی، تعریف مجانب افقی و مجانب قائم به شرح زیر است.
است. بطور کلی، تعریف مجانب افقی و مجانب قائم به شرح زیر است.
تعریف مجانب های افقی و قائم
خط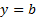 مجانب افقی نمودار تابع
مجانب افقی نمودار تابع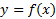 است اگر داشته باشیم
است اگر داشته باشیم
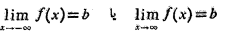
خط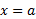 مجانب قائم نمودار تابع است اگر داشته باشیم.
مجانب قائم نمودار تابع است اگر داشته باشیم.
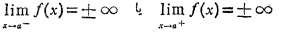
 مثال
مثال
شکل زیر نمودار
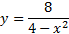
را نشان می دهد. خط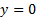 یک مجانب سمت راست است زیرا وقتی
یک مجانب سمت راست است زیرا وقتی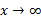 ،
،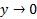 و یک مجانب سمت چپ هم هست زیرا وقتی
و یک مجانب سمت چپ هم هست زیرا وقتی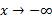 ،
،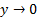 .
.
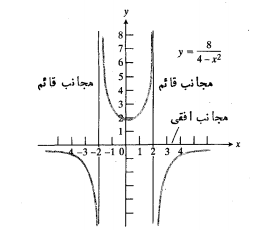
خط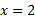 یک مجانب قائم است زیرا
یک مجانب قائم است زیرا
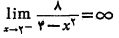
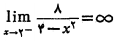
و نیز زیرا
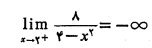
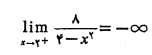
به همین ترتیب خط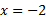 یک مجانب قائم است زیرا وقتی
یک مجانب قائم است زیرا وقتی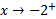 ،
،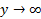 و نیز وقتی
و نیز وقتی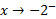 ،
،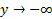 .
.
مجانب های مایل
اگر تابعی گویا خارج قسمت دو چند جمله ای باشد که عامل مشترک نداشته باشند، و اگر درجه صورت، یک واحد بیشتر از درجه مخرج باشد، آنگاه نمودار یک مجانب مایل دارد. برای مثال تابع
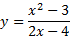
یک مجانب مایل دارد شکل زیر. برای مشاهده دلیل این امر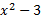 را بر
را بر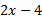 تقسیم می کنیم.
تقسیم می کنیم.
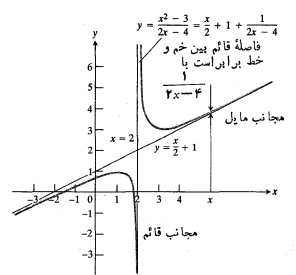
بنابراین داریم
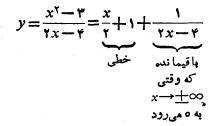
به این ترتیب می بینیم که
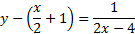
و
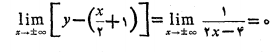
پس فاصله قائم بین خم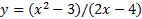 و خط
و خط 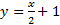 وقتی
وقتی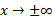 ، به صفر میل می کند. بنابراین خط
، به صفر میل می کند. بنابراین خط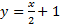 مجانب خم است.
مجانب خم است.
توجه کنید که وقتی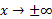 شیب خم یعنی
شیب خم یعنی
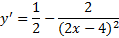
به 2/1 میل می کند که شیب خط است. خط در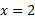 مجانب قائم نیز دارد.
مجانب قائم نیز دارد.
 مثال: نموار تابع زیر را رسم کنید.
مثال: نموار تابع زیر را رسم کنید.
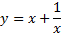
حل: برای رسم نمودار، تقارن، مجانب ها، صعود و نزول، تقعر را در نظر می گیریم.
تقارن، این تابع فرد است؛ لذا نمودارش نسبت به مبدا متقارن است.
مجانب ها، اگر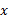 از سمت راست به 0 میل کند، آنگاه
از سمت راست به 0 میل کند، آنگاه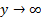 . اگر
. اگر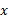 از سمت چپ به 0 میل کند، آنگاه
از سمت چپ به 0 میل کند، آنگاه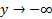 . خط
. خط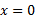 مجانب قائم است.
مجانب قائم است.
وقتی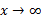 ،
،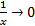 و
و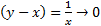 بنابراین، خط
بنابراین، خط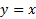 نیز مجانب نمودار است.
نیز مجانب نمودار است.
صعود و نزول. مشتق اول،
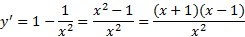
وقتی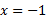 و
و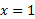 ، برابر با صفر است، و در
، برابر با صفر است، و در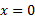 تعریف نمی شود. مشتق وقتی
تعریف نمی شود. مشتق وقتی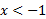 مثبت ، وقتی
مثبت ، وقتی
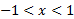 و
و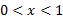 منفی، و وقتی
منفی، و وقتی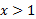 ، مثبت است (شکل زیر).
، مثبت است (شکل زیر).
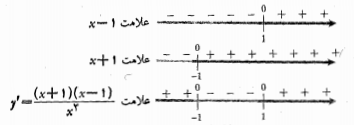
لذا نمودار بر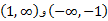 صعود می کند، و بر
صعود می کند، و بر 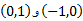 نزول می کند. این تابع در
نزول می کند. این تابع در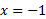 یک مقدار ماکسیمم موضعی دارد زیرا در این نقطه
یک مقدار ماکسیمم موضعی دارد زیرا در این نقطه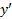 از + به 1- تغییر می کند، و در
از + به 1- تغییر می کند، و در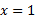 که
که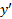 از – به + تغییر می کند یک مقدار مینیمم موضعی دارد.
از – به + تغییر می کند یک مقدار مینیمم موضعی دارد.
تقعر، مشتق دوم؛
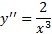
وقتی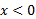 منفی، و وقتی
منفی، و وقتی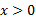 مثبت است. پس وقتی
مثبت است. پس وقتی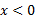 تقعر خم رو به پایین ، و وقتی
تقعر خم رو به پایین ، و وقتی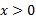 تقعر آن رو به بالا است.
تقعر آن رو به بالا است.
توصیه می کنیم جهت یاد گیری مباحث بیشتر ریاضیسایت لینوم از محصول کپسول آموزشی ریاضی 1 استفاده کنید.