آهنگ تغییر تابع
در اینآموزش ریاضی یکلینوم قصد داریم نظری به سرعت و سایر نمونه های آهنگ تغییر بیندازیم و قضیه ای را بیان کنیم که به کمک آن بتوان حد را به سرعت و با کمترین زحمت محاسبه نمود. برای شروع این بحث به توضیحاتی در مورد مختصات برای صفحه، شیب خط، معادله های خط، تابع و نمودار، قدر مطلق می پردازیم.
1.مختصات برای صفحه
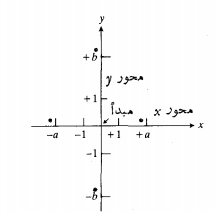
بحث هندسه تحلیلی با انتساب مختصات عددی به همه نقاط واقع در یک صفحه آغاز می شود. برای انتساب مختصات به نقاط واقع در صفحه، دو خط اعداد در نظر می گیریم که در نقاط صفرخود، یکدیگر را به زاویه قائمه قطع کنند.
روی محور X ، عدد مثبت a به فاصله a واحد در سمت راست مبدا قرار دارد و عدد منفی a – به فاصله a واحد در سمت چپ مبدا واقع است. روی محور y، عدد مثبت b به فاصله b واحد بالای مبدا و عدد منفی b- به فاصله b واحد پایین مبدا قرار دارد. درمختصات دکارتی، درجه بندی هریک از محورها نسبت به مبدا متقارن است.
شیوه ی معمولیترسیم دو خط به شکل زیر است. جفت (a,b) به نقطه ای نسبت داده می شود که در آنجا، عمود بر محور X در a، عمود بر محورy در b را قطع می کند. عدد a، عدد واقع در پای عمودی است که از p بر محور X رسم می شود. عدد b عدد واقع در پای عمود از p بر محور y است. عدد a از محور X، مختص X نقطه p است. عدد b از محور y، مختص y نقطه p است. جفت (a,b)، جفت مختصات نقطه p است که یک جفت مرتب می باشد.
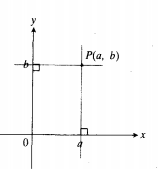
می توان شیوه ای را که به هر نقطه صفحه، یک جفت مرتب از اعداد حقیقی را نسبت می دهد معکوس کرد، تا به هر جفت مرتب ازاعداد حقیقی، نقطه ای در صفحه نسبت داده شود. نقطه ای که به جفت 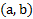 منسوب می شود، محل تقاطع عمود بر محور Xدر a با عمود بر محور y در b است. بنا براین انتساب مختصات، تناظر یک به یکی بین نقاط صفحه و مجموعه همه جفت های مرتب اعداد حقیقی است. می توان گفت که هر نقطه، یک جفت دارد و هر جفت، یک نقطه دارد.
منسوب می شود، محل تقاطع عمود بر محور Xدر a با عمود بر محور y در b است. بنا براین انتساب مختصات، تناظر یک به یکی بین نقاط صفحه و مجموعه همه جفت های مرتب اعداد حقیقی است. می توان گفت که هر نقطه، یک جفت دارد و هر جفت، یک نقطه دارد.
نقاط روی محورهای مختصات دو نوع نشانه عددی دارند: اعداد منفردی از محورها و جفت هایی از اعداد از صفحه. هر نقطه روی محور X، مختص y اش صفر است و هر نقطه روی محور y، مختصات X اش صفر است. مختصات مبدا عبارت اند از(0,0).
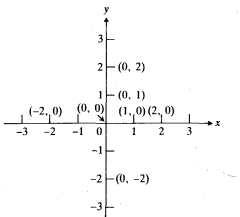
جهت، و ربع صفحه
حرکت بر روی محور Xاز چپ به راست، حرکت درجهت مثبت Xنامیده می شود. حرکت از راست به چپ، حرکت در جهت منفی X است. بر روی محور y، جهت مثبت به سمت بالا و جهت منفی به سمت پایین است. مبدا محور Xرا به دو قسمت تقسیم می کند: قسمت مثبت محور X در سمت راست مبدا و قسمت منفی محور X در سمت چپ مبدا. همچنینمبدا محور y را به قسمت مثبت محور y و قسمت منفی محور y تقسیم می کند.

محورها صفحه را به چهار ناحیه یا ربع تقسیم می کند. جهت روی محورها، X و y در جهت مثبت افزایش و درجهت منفی کاهش می یابند. در شکل زیر ربع ها با عدد رومی نشان داده شده است.

2.شیب خط
شیب خط های غیر قائم
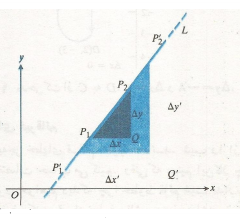
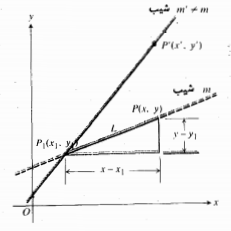
همه خط ها به جزخط های قائم، شیب دارند. شیب را از روی تغییرات مختصات حساب می کنیم. ابتدا فرض کنید L یک خط غیر قائم در صفحه باشد. نیز فرض کنید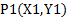 و
و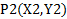 دو نقطه روی L باشند.
دو نقطه روی L باشند.
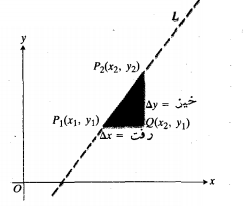
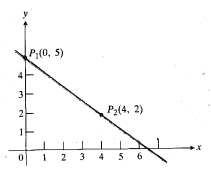
چون L قائم نیست،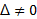 و می توانیم شیب L را به صورت
و می توانیم شیب L را به صورت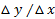 تعریف کنیم، یعنی مقدار خیز در واحد رفت. مرسوم است که شیب را با حرفm نشان می دهند.
تعریف کنیم، یعنی مقدار خیز در واحد رفت. مرسوم است که شیب را با حرفm نشان می دهند.
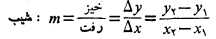
فرض کنید در محاسبه شیب در معادله بالابه جای نقاط y1 و y2 ، زوج دیگری از نقاط مثلا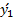 و
و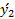 را روی L در نظر بگیریم.
را روی L در نظر بگیریم.
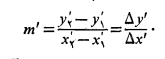
برابرند زیرا نسبت های اضلاع متناظر از مثلث های متشابه اند  اعداد
اعداد
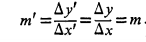
شیب یک خط به سرعت بالارفتن و پایین آمدن خط بستگی دارد و نه به نقاطی که برای محاسبه شیب به کار می بریم
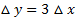 به سمت بالا امتدا می یابد دارایشیب مثبت است. به این معنی است که برای هر تغییر مکان روی خط داریم xخطی که با افزایش
به سمت بالا امتدا می یابد دارایشیب مثبت است. به این معنی است که برای هر تغییر مکان روی خط داریم xخطی که با افزایش
خطی که با افزایش 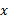 به سمت پایین امتداد می یابد دارای شیب منفی است. در شکل شیب خط افقی صفر است. همه نقاط روی این خط دارای مختص
به سمت پایین امتداد می یابد دارای شیب منفی است. در شکل شیب خط افقی صفر است. همه نقاط روی این خط دارای مختص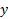 واحدی هستند بنابراین 0
واحدی هستند بنابراین 0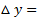
فرمول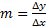 را د رمورد خط های قائم نمی توان به کار برد زیرا
را د رمورد خط های قائم نمی توان به کار برد زیرا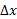 روی هرخط قائم برابر صفر است. وقتی
روی هرخط قائم برابر صفر است. وقتی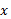 به اندازه 4 واحد افزایش می یابد
به اندازه 4 واحد افزایش می یابد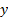 به اندازه 3 واحد کاهش پیدا می کند.
به اندازه 3 واحد کاهش پیدا می کند.
خط هایی که با هم موازی یا برهم عمودند
خط های موازی، زوایای میل مساوی دارند. از این رو اگر قائم نباشند شیب آن ها یکی است. برعکس، خط هایی کهشیب مساوی دارند زوایای میل آن ها برابر است و بنابراین با هم موازی اند.
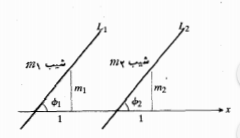
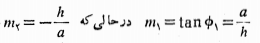
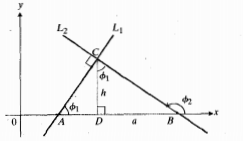
اگر هیچ یک از دو خط عمود برهم L1وL2 قائم نباشد، شیب های آن ها m1 و m2 با معادله 1-=m1 m2 به هم مربوط می شوند. با
با متشابه است. ازاین رو،ϕ1
متشابه است. ازاین رو،ϕ1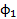 زاویه بالایی
زاویه بالایی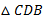 نیز هست. با توجه به اضلاع
نیز هست. با توجه به اضلاع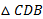 داریم
داریم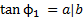 بنابراین.
بنابراین.
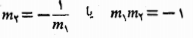
3.معادله های خط
معادله یک خط، معادله ای است که مختصات نقاط واقع بر خط در آن صدق کنند و مختصات نقاطی که برخط قرار ندارند در آن صدق نکنند. این گونه معادلات نشان می دهند که چگونه مقدار y را به ازای هر مقدار x روی یک خط غیرقائم یا مقدار x را به ازای هر مقدار y روی یکخط غیرافقی حساب کنیم.
خط های قائم
هر خط قائم L باید محور x را در نقطه ای چون( a,0) قطع کند. سایر نقاط روی L ، در امتداد مستقیم، بالا یا پایین ( a,0) قرار دارند. یعنی که اولین مختصات هر نقطه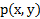 روی L ، باید a باشد در حالی که y می تواند هر عددی باشد. به عبارتی دیگر مختصات تمام نقاط
روی L ، باید a باشد در حالی که y می تواند هر عددی باشد. به عبارتی دیگر مختصات تمام نقاط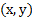 روی L در معادله a = x صدق می کنند.
روی L در معادله a = x صدق می کنند.
برای اینکه مطمئن شویم a = x یک معادله L است، باید بدانیم که نقاط غیر واقع بر L مختصات اولشان متفاوت با a است. قطعا درست است زیرا عمودهایی که از این نقاط بر محور x رسم شوند، این محور را در نقطه a = x قطع نمی کنند.
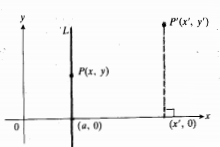
معادله متعارف خط قائم گذرنده از نقطه (a,b) عبارت است از x=a0
آموزش گام به گام این مبحث ریاضی1
خط های غیر قائم
برای نوشتن معادله خطی مانند L که قائم نیست، باید شیبm ومختصات یک نقطه 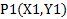 روی آن خط را بدانیم. اگر
روی آن خط را بدانیم. اگر 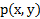 نقطه دیگری روی L باشد. آنگاه x
نقطه دیگری روی L باشد. آنگاه x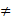 x1و می توانیم شیب L را به صورت
x1و می توانیم شیب L را به صورت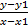 بنویسیم.
بنویسیم.
سپس می توانیم این عبارت را مساوی m قرار دهیم و عبارت m =y-y1x-x1 را بدست آوریم.
اگر دو طرف معادله m = 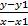 را در x-x1 ضرب کنیم معادله
را در x-x1 ضرب کنیم معادله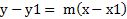 بدست می آید.این یک معادله L است.
بدست می آید.این یک معادله L است.
طول از مبدا و عرض از مبدا
مختص نقطه ای که یک خط در آنجا محور
نقطه ای که یک خط در آنجا محور 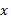 را قطع می کند، طول از مبدا آن خط نامیده می شود. برای یافتن آن درمعادله خط قرار می دهیم y=0 و معادله را نسبت بهx حل می کنیم. مختص y نقطه ای که یک خط در آنجا محور y را قطع می کند، عرض از مبدا آن خط نامیده می شود. برای یافتن آن، در معادله خطx=0 را قرار داده و معادله را نسبت به y حل می کنیم.
را قطع می کند، طول از مبدا آن خط نامیده می شود. برای یافتن آن درمعادله خط قرار می دهیم y=0 و معادله را نسبت بهx حل می کنیم. مختص y نقطه ای که یک خط در آنجا محور y را قطع می کند، عرض از مبدا آن خط نامیده می شود. برای یافتن آن، در معادله خطx=0 را قرار داده و معادله را نسبت به y حل می کنیم.
هر خطی که قائم نباشد باید محور y را در نقطه ای چون (0,b) قطع کند. عدد b، عرض از مبدا خط است. اگر در معادله 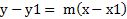 قرار دهیم
قرار دهیم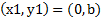 ، معادله خط شیب دست می آید:
، معادله خط شیب دست می آید: 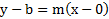 که معادل با
که معادل با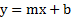 است.
است.
این معادله "شیب-عرض از مبدا" خط نامیده می شود.

مثلا برای ترسیم نمودار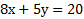 ، نقاط تقاطع با محورها را مشخص می کنیم و خطی از نقاط مشخص شده می گذرانیم.روشی برای ترسیم سریع نمودار خط این است که نقاط تقاطع خط با محورها را مشخص کنیم و خطی از نقاط مشخص شده بگذرانیم. این روش تنها وقتی کارایی ندارد که خط از مبدا بگذرد که در این صورت، به جای دو نقطه تقاطع، یک نقطه خواهیم داشت و یا اینکه مشخص کردننقاط تقاطع در شکل دشوار باشد.
، نقاط تقاطع با محورها را مشخص می کنیم و خطی از نقاط مشخص شده می گذرانیم.روشی برای ترسیم سریع نمودار خط این است که نقاط تقاطع خط با محورها را مشخص کنیم و خطی از نقاط مشخص شده بگذرانیم. این روش تنها وقتی کارایی ندارد که خط از مبدا بگذرد که در این صورت، به جای دو نقطه تقاطع، یک نقطه خواهیم داشت و یا اینکه مشخص کردننقاط تقاطع در شکل دشوار باشد.
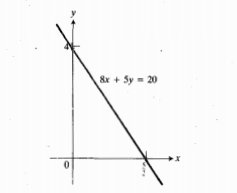
خط های افقی
وقتی خط 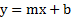 افقی باشد، m=0 و معادله به صورت ساده y=b در می آید. معادله متعارف خط افقی گذرنده از (a,b) عبارت از y = b.
افقی باشد، m=0 و معادله به صورت ساده y=b در می آید. معادله متعارف خط افقی گذرنده از (a,b) عبارت از y = b.
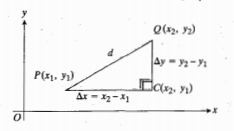
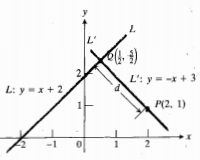
فاصله یک نقطه تا یک خط
برای محاسبه فاصله بین نقاط 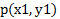 و
و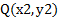 فرمول زیر را استفاده می کنیم.
فرمول زیر را استفاده می کنیم.
برای محاسبه فاصله نقطه ای چون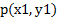 تا خطی مثل L ، نقطه
تا خطی مثل L ، نقطه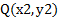 در پای عمود وارد از p بر Lرا پیدا کرده و فاصله p تا Q را حساب می کنیم. d فاصله بین دو نقطه
در پای عمود وارد از p بر Lرا پیدا کرده و فاصله p تا Q را حساب می کنیم. d فاصله بین دو نقطه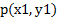 و
و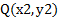 ، با به کاربردنقضیه فیثاغورس در مورد مثلث قائم الزاویه PCQ محاسبه می شود. چون
، با به کاربردنقضیه فیثاغورس در مورد مثلث قائم الزاویه PCQ محاسبه می شود. چون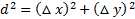 داریم.
داریم.
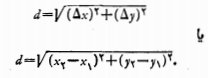
معادله کلی خط
معادله Ax + By = C معادله خط کلی نمامیده می شود که در آن A وB هر دو صفر نیستند. نمودار این معادله همیشه یک خط است و نیز هر خطی معادله اش به این صورت است. معادله های خط شامل موارد زیر است.
| خط قائم گذرنده از(a,b)
| x=a |
| خط افقی گذرنده از(a,b)
| Y=b |
| معادله شیب-عرض از مبدا
| Y=mx + b |
| معادله نقطه-شیب
| y-y1=m(x- x1) |
| معادله کلی خط | Ax + By = C |
4.تابع و نمودار
هر تابع از مجموعه ای چون D به مجموعه ای چون R، قاعده ای است که به هر عنصر D تک عنصری از R را منسوب می کند. منظور از کلمه تک این است که به هر ورودی از دامنه دقیقا یک خروجی از بُرد نسبت داده می شود، نه کمتر و نه بیشتر.
به عبارت دیگر هر ورودی در فهرست جفت های ورودی – خروجی که به وسیله تابع تعریف می شود، دقیقا یک بار ظاهر می شود. عبارت ریاضی این تعریف به شکل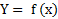 می باشد.
می باشد.
نمودار و ترسیم آن
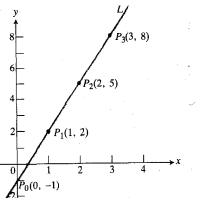
نقاطی از صفحه که جفت های مختصات ان ها جفت های ورودی- خروجی یک تابع هستند،نمودار تابع را تشکیل می دهند. مثلا خط L در شکل نمودار تابع 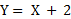 است. زیرا مجموعه نقاطی ازصفحه است که جفت های مختصات
است. زیرا مجموعه نقاطی ازصفحه است که جفت های مختصات 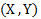 آن ها زوج های ورودی – خروجی این تابع هستند.
آن ها زوج های ورودی – خروجی این تابع هستند.
انتخاب نقاط برای ترسیم نمودار
برای ترسیم نمودار باید مراحل زیر را به ترتیب انجام داد.
باید مراحل زیر را به ترتیب انجام داد.
- نقاط تماس یا تقاطع نمودار با محورها را مشخص کنید. این نقاط با قرار دادن Y=0 و X= 0 در معادله
 به راحتی بدست می آید.
به راحتی بدست می آید. - چند نقطه نزدیک مبدا را مشخص کنید. معمولا وقتی مقادیر X کوچک هستند، مقادیر Y براحتی محاسبه می شوند.
- نمودار تابع را در نقاط انتهایی دامنه اش یا در نزدیکی ان ها رسم کنید.
در شکل های زیر نمودارهای تابع های مثال های زیر نشان داده شده است.
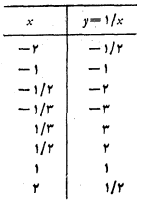
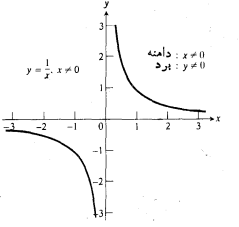
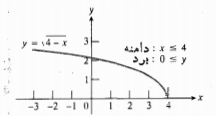
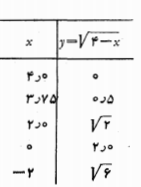
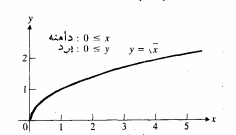
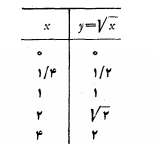
5.قدر مطلق
تابع قدر مطلق
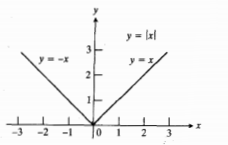
قدر مطلق عددی مانند X ، عدد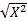 است. اگر X مثبت باشد، قدر مطلق آن همان X است. ولی اگر X منفی باشد، قدر مطلق آن X- است. اگر X صفر باشدقدر مطلق آن صفر است. نماد قدر مطلق
است. اگر X مثبت باشد، قدر مطلق آن همان X است. ولی اگر X منفی باشد، قدر مطلق آن X- است. اگر X صفر باشدقدر مطلق آن صفر است. نماد قدر مطلق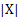 است و تابع آن به صورت زیر می باشد. نمودار تابع
است و تابع آن به صورت زیر می باشد. نمودار تابع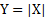 به شکل زیر رسم شده است.
به شکل زیر رسم شده است.
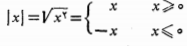
نکته مهم : قدر مطلق مجموع دو عدد هیچ گاه بزرگتر از مجموعقدر مطلق های آن ها نخواهد بود.
ویژگی های عددی قدر مطلق
در ویژگی های عددی قدرمطلق که در ادامه بیان می شوند برای اعداد a وb بر قرار هستند.
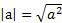
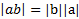
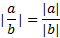
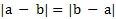
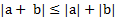
بازه و قدر مطلق
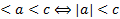
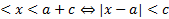
برای تسلط بیشتر بر این مباحث، میتوانید کپسول آموزشی ریاضی یک لینوم را مشاهده کنید.