روش جانشانی در انتگرال گیری
اغلب با تعویض متغیر می توانیم یک انتگرال نا آشنا را به انتگرالی تبدیل کنیم که روش محاسبه آن را می دانیم. روش انجام دادن این کار را روش جانشانی در انتگرال گیری می نامند.
این روش یکی از روش های اصلی محاسبه انتگرال ها است. نخست چگونگی کار کرد روش و سپس علت ثمر بخش بودن آن را نشان می دهیم.
 مثال 1 برای محاسبه
مثال 1 برای محاسبه
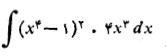
این مراحل را طی می کنیم
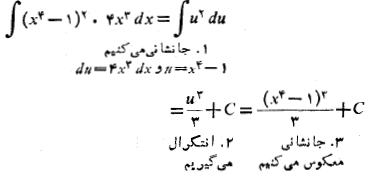
این روش ثمربخش است زیرا
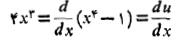
بخشی از انتگرالده است. به کمکقاعده زنجیری داریم
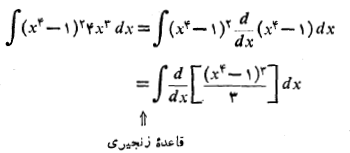
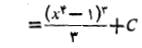
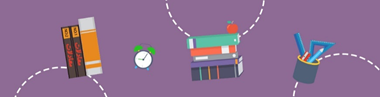
 مثال 2 برای محاسبه
مثال 2 برای محاسبه
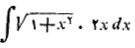
این مراحل را طی می کنیم
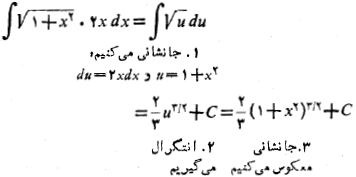
این روش اثربخش است زیرا
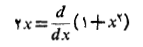
بخشی از انتگرالده است. به کمک قاعده زنجیری داریم
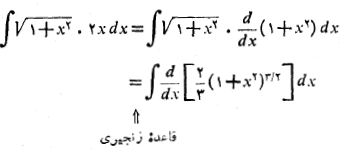
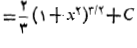
قاعده ای که در مثال های 1و2 به کار رفت چنین است
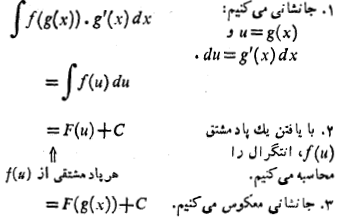
این سه مرحله، مراحل روش جانشانی در انتگرال گیری اند.
روش جانشانی در انتگرال گیری
برای محاسبه انتگرال
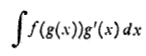
که در آن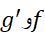 توابعی پیوسته اند،مراحل زیر را طی کنید.
توابعی پیوسته اند،مراحل زیر را طی کنید.
1.جانشان های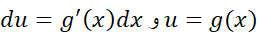 را انجام دهید تاانتگرال زیر به دست آید
را انجام دهید تاانتگرال زیر به دست آید
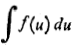
2.نسبت بهu انتگرال بگیرید.
انتگرال بگیرید.
3.در نتیجه به دست آمدهg(x) را به جایu بگذارید.
بگذارید.
 مثال 3 انتگرال زیر را حساب کنید
مثال 3 انتگرال زیر را حساب کنید
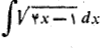
حل: چنین جانشانی می کنیم
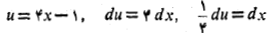
بنابراین
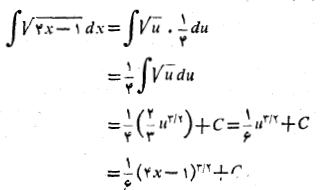
 مثال 4 انتگرال زیر را حساب کنید
مثال 4 انتگرال زیر را حساب کنید
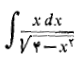
حل: چنین جانشانی می کنیم
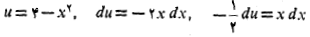
بنابراین
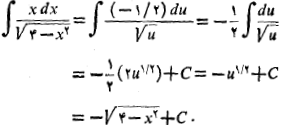
چنانکه مثال بعد نشان می دهد برای جانشانی موفق، بیش از یک راه وجود دارد.
 مثال 5 انتگرال زیر را حساب کنید
مثال 5 انتگرال زیر را حساب کنید
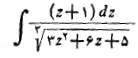
حل: روش جانشانی را می توان به عنوان یک ابزار اکتشافی به کاربرد: پیچیده ترین بخش انتگرالده را انتخاب می کنیم، و جانشینی برای آن در نظر می گیریم.
در این مثال می توان 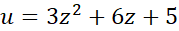 و یا حتی اگر بخت یاری کند
و یا حتی اگر بخت یاری کند
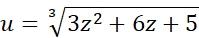 را آزمود. در این صورت آنچه پیش می آید چنین است.
را آزمود. در این صورت آنچه پیش می آید چنین است.
جانشانی های زیر را انجام می دهیم
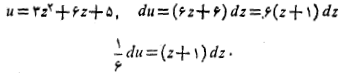
در این صورت داریم
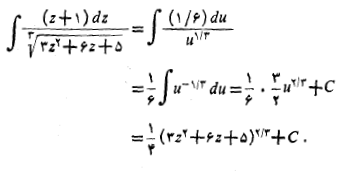
جانشانی های زیر را انجام می دهیم
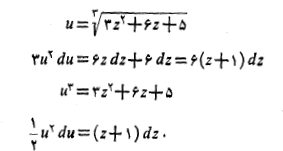
آنگاه داریم
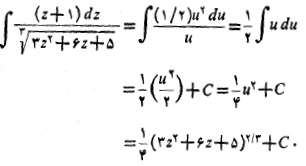
علت درستی روش جانشانی
اگر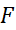 پاد مشتقی از
پاد مشتقی از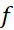 باشد، بنا به قاعده زنجیری داریم
باشد، بنا به قاعده زنجیری داریم
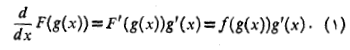
بنابراین
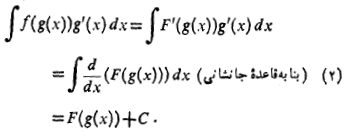
با قرار دادن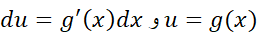 در انتگرال همین نتیجه به دست می آید
در انتگرال همین نتیجه به دست می آید
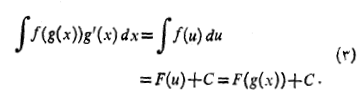

فرمول های انتگرال ها با استفاده از نمادهای دیفرانسیلی
به کمک نمادهای دیفرانسیلی می توان فرمول انتگرال ها را ساده تر بیان کرد.
مثلا 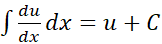 به صورت
به صورت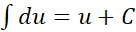 در می آید.
در می آید.
و
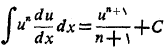 به صورت
به صورت 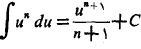 ،
،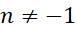 در می آید.
در می آید.
همچنین
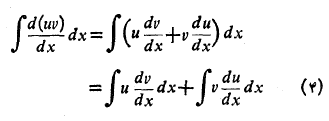
به این صورت در می آید:
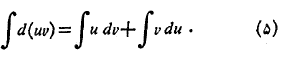
انتگرال تابع های مثلثاتی
از فرمول هایمشتق
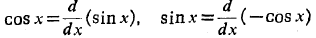
فرمول های انتگرال گیری زیر را به دست می آوریم
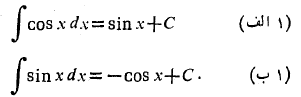
اگر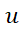 تابعی مشتق پذیر از
تابعی مشتق پذیر از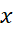 باشد، با به کار بردن قاعده زنجیری در مورد
باشد، با به کار بردن قاعده زنجیری در مورد 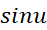 داریم
داریم
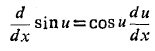
با جابه جا کردن طرفین تساوی چنین به دست می آید
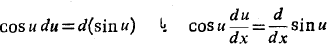
پس
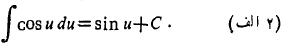
همچنین

و بنابراین
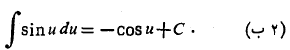
به کمک رابطه های (1) و (2) می توان بسیاری ازانتگرال های مثلثاتی را حساب کرد.
 مثال 1 انتگرال زیر را حساب کنید
مثال 1 انتگرال زیر را حساب کنید
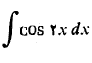
حل: جانشانی های زیر را به کار می بریم
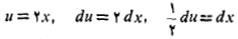
بنابراین
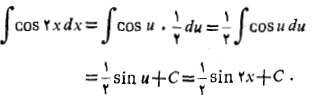
 مثال 2 انتگرال زیر را حساب کنید
مثال 2 انتگرال زیر را حساب کنید
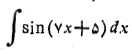
حل: با جانشانی های
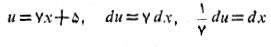
داریم
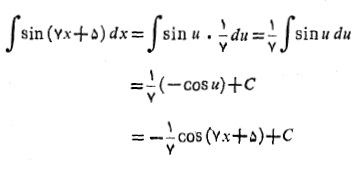
 مثال3 انتگرال زیر را حساب کنید
مثال3 انتگرال زیر را حساب کنید
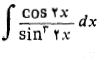
حل: با جانشانی های
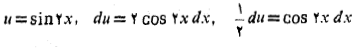
داریم
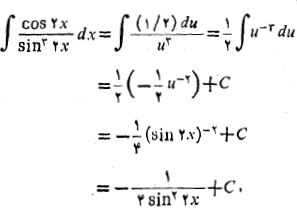
ممکن است بیش از یک راه برای یک جانشانی موفق وجود داشته باشد. در مثال زیر برای جانشانی بخش پیچیده انتگرال از دو راه بهره می گیریم که هر دو راه قرین موفقیت اند.
 مثال4 انتگرال زیر را حساب کنید
مثال4 انتگرال زیر را حساب کنید
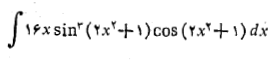
حل: با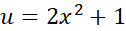 . با جانشانی های
. با جانشانی های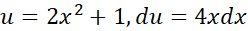
داریم
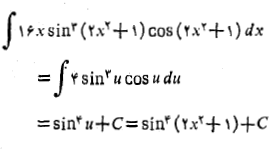
حل: با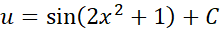 . با جانشانی های
. با جانشانی های
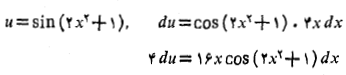
داریم
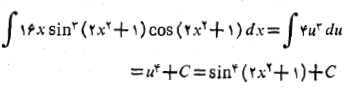
 مثال5 انتگرال زیر را حساب کنید
مثال5 انتگرال زیر را حساب کنید
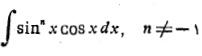
حل: با جانشانی های
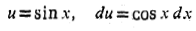
داریم

 مثال6 انتگرال زیر را حساب کنید
مثال6 انتگرال زیر را حساب کنید
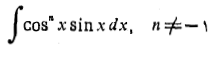
حل: با جانشانی های
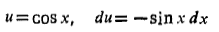
داریم
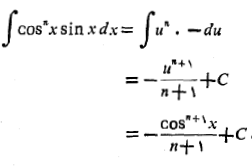
اگر در مثال های 5و6،n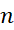 برابربا 1-می بود با انتگرال ها چه می کردیم؟ به ازای
برابربا 1-می بود با انتگرال ها چه می کردیم؟ به ازای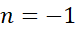 این انتگرال ها به این صورت در می آیند:
این انتگرال ها به این صورت در می آیند:
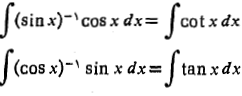
با اینکه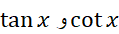 پاد مشتق دارند، نمی توانیم آن ها را بر حسب توابعی که فعلا می شناسیم بیان کنیم. بنابراین باید با تابع لگاریتمی طبیعی و انتگرال ها آشنا شویم.
پاد مشتق دارند، نمی توانیم آن ها را بر حسب توابعی که فعلا می شناسیم بیان کنیم. بنابراین باید با تابع لگاریتمی طبیعی و انتگرال ها آشنا شویم.
انتگرال تابع های مثلثاتی دیگر
با استفاده از فرمول هایمشتق تابع های نانژانتی، کتانژانتی، سکانتی و کسکانتی،فرمول های انتگرالی زیر را به دست می آیند.
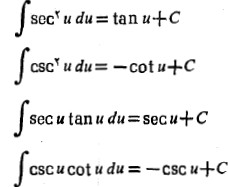
در همه فرمول هاu باید تابعی مشتق پذیر ازx
باید تابعی مشتق پذیر ازx باشد. درستی هر فرمول را می توان با مشتق گیری ازطرف چپ فرمول نسبت بهx
باشد. درستی هر فرمول را می توان با مشتق گیری ازطرف چپ فرمول نسبت بهx بررسی کرد. در هر مورد برای به دست آوردن انتگرالده طرف چپ، قاعده زنجیری به کار می رود.
بررسی کرد. در هر مورد برای به دست آوردن انتگرالده طرف چپ، قاعده زنجیری به کار می رود.
 مثال7
مثال7
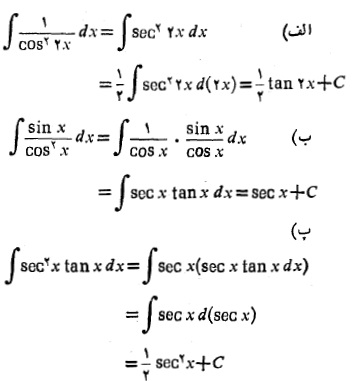
 مثال 8 انتگرال زیر را حساب کنید
مثال 8 انتگرال زیر را حساب کنید
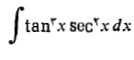
حل: با جانشانی های
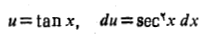
داریم
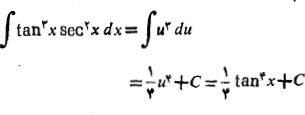
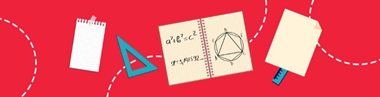
استفاده از اتحاد های مثلثاتی
برای تبدیل یک انتگرال نا آشنا به انتگرالی که بتوان آن را محاسبه کرد، اغلب می توان ازاتحادهای مثلثاتی استفاده کرد. اینک چند مثال می آوریم.
 مثال9 انتگرال زیر را حساب کنید
مثال9 انتگرال زیر را حساب کنید
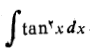
حل: اتحاد 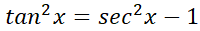 را به کار می بریم
را به کار می بریم
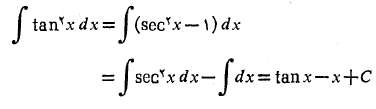
 مثال 10 انتگرال زیر را حساب کنید
مثال 10 انتگرال زیر را حساب کنید
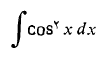
حل: با استفاده از فرمول دو برابر زاویه،
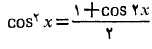
داریم
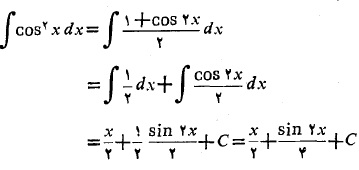
 مثال11 انتگرال زیر را حساب کنید
مثال11 انتگرال زیر را حساب کنید
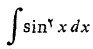
حل: با استفاده از فرمول دو برابر زاویه،
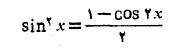
داریم
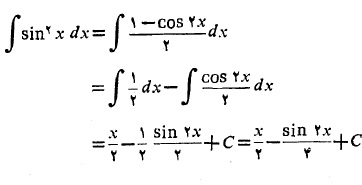
 مثال12 انتگرال زیر را حساب کنید
مثال12 انتگرال زیر را حساب کنید
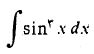
حل: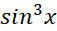 را چنین می نویسیم
را چنین می نویسیم
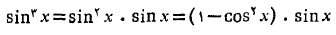
بنابراین
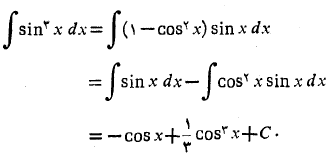
برای محاسبه انتگرال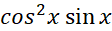 نسبت به
نسبت به 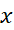 از نتیجه مثال 6 استفاده کرده ایم.
از نتیجه مثال 6 استفاده کرده ایم.
انتگرال معین: مساحت ناحیه زیر یک خم
اکنون به نوع دیگری از انتگرال گیری یعنی انتگرال گیری به کمک مجموعیابی می پردازیم. این انتگرال ها، انتگرال های معین نامیده می شوند تا از انتگرال های نامعین متمایز باشند.
انتگرال معین یک حد عددی است . دسته ای از پاد مشتق ها نیست؛ و ممکن است تعجب کنید که چرا این دو مقوله متفاوت ریاضی انتگرال نام دارند و ارتباط بین آن ها چیست.
روشی که برای این نوع انتگرال گیری اتخاذ می کنیم چنین است که نخست به تعریف مساحت ناحیه محصور بین نمودار یک تابع پیوسته نامنفی مانند
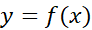 و بازه ای از محور
و بازه ای از محور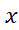 مانند
مانند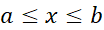 می پردازیم.
می پردازیم.
در آغاز تا آنجا که می توانیم، طبق شکل زیر، بخش هر چه بیشتری از ناحیه را با مستطیل های محاطی قائم پر می کنیم. مجموع مساحت های مستطیل ها تقریبی است از مساحت ناحیه.
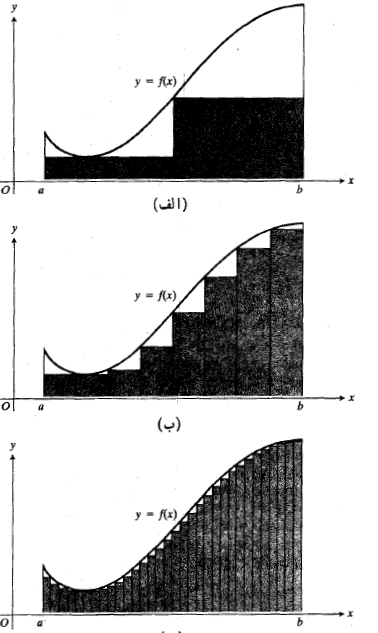
هرچه تعداد مستطیل ها بیشتر باشد، تقریب بهتری به دست می آید. بنا به تعریف، مساحت این ناحیه، حد مجموع مساحت های مستطیل ها است وقتی که مستطیل ها کوچک و کوچکتر شوند و تعداد آن ها به سوی بینهایت میل کند.
پس از اینکه بیان دقیق ریاضی این مطلب را ارائه کردیم دو موضوع روشن خواهند شد. نخست اینکه اگر به جای مستطیل های محاطی، مستطیل های محیطی در شکل زیر و یا هر نوع مستطیل های دیگری که قاعده پایین آن ها بر محور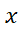 منطبق باشد و قاعده بالای آن ها خم را قطع کند به کار بریم دقیقا همان حد به دست می آید.
منطبق باشد و قاعده بالای آن ها خم را قطع کند به کار بریم دقیقا همان حد به دست می آید.
دوم اینکه،حد مجموع مساحت های این مستطیل ها نه تنها برای توابع پیوسته نامنفی،که بحث خود را با آن ها آغاز کردیم، بلکه برای هر تابع پیوسته ای وجود دارد.
تقریب زدن مساحت به کمک مستطیل ها
فرض می کنیم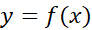 تابعی پیوسته و نامنفی روی بازه بسته
تابعی پیوسته و نامنفی روی بازه بسته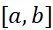 باشد. می خواهیم مساحت ناحیه محدود به نمودار
باشد. می خواهیم مساحت ناحیه محدود به نمودار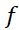 ، خطوط
، خطوط 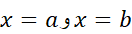 ، و محور
، و محور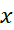 را تعریف کنیم. این ناحیه را ناحیه زیر خم
را تعریف کنیم. این ناحیه را ناحیه زیر خم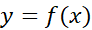 از
از 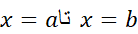 می نامیم.
می نامیم.
کار را با یک برآورد شروع می کنیم. بدین منظور، ناحیه را به کمک خطوط عمود بر محور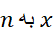 نوار نازک با پهنای یکسان
نوار نازک با پهنای یکسان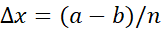 تقسیم می کنیم. این خطوط از نقاط انتهایی
تقسیم می کنیم. این خطوط از نقاط انتهایی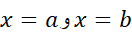 و نقاط میانی بسیاری که آن ها را با
و نقاط میانی بسیاری که آن ها را با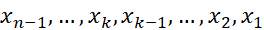 نشان می دهیم می گذرند براساس شکل زیر.
نشان می دهیم می گذرند براساس شکل زیر.

هر نوار را با مستطیلی محاطی تقریب می زنیم که از قاعده پایینی نوار که بر محور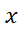 واقع است تا پایین ترین نقطه خم که در بالای این قاعده قرار دارد امتداد می یابد.
واقع است تا پایین ترین نقطه خم که در بالای این قاعده قرار دارد امتداد می یابد.
اگر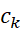 نقطه ای باشد که در آن مقدار تابع
نقطه ای باشد که در آن مقدار تابع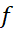 در بازه از
در بازه از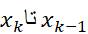 مینیمم باشد (چنین نقطه ای وجود دارد زیرا
مینیمم باشد (چنین نقطه ای وجود دارد زیرا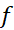 پیوسته است)، ارتفاع این مستطیل
پیوسته است)، ارتفاع این مستطیل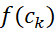 است. مساحت این مستطیل، حاصل ضرب ارتفاع در طول قاعده آن است
است. مساحت این مستطیل، حاصل ضرب ارتفاع در طول قاعده آن است
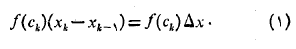
بنابراین، در شکل فوق مساحت اولین مستطیل محاطی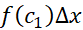 ، مساحت مستطیل دوم
، مساحت مستطیل دوم 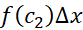 و به همین ترتیب، مساحت مستطیلn ام یا آخر
و به همین ترتیب، مساحت مستطیلn ام یا آخر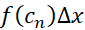 است. مجموع این مساحت ها یعنی
است. مجموع این مساحت ها یعنی
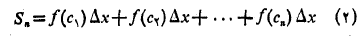
مقدار تقریبی مساحت ناحیه زیرخم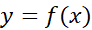 از
از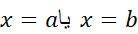 را به دست می دهد.
را به دست می دهد.
 مثال1 مساحت ناحیه زیرخم
مثال1 مساحت ناحیه زیرخم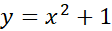 از
از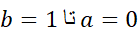 را با
را با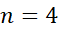 مستطیل محاطی برآورد کنید.
مستطیل محاطی برآورد کنید.
حل: خم را در بازه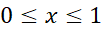 رسم می کنیم مطابق شکل.
رسم می کنیم مطابق شکل.
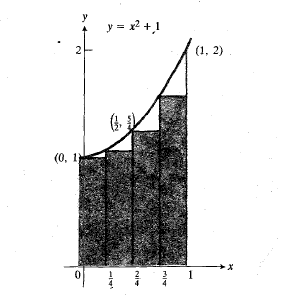
سپس بازه را به کمک نقاط زیر به چهار بخش تقسیم می کنیم
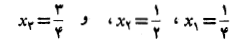
طول هرزیر بازه برابر است با∆x=1/4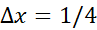 . مستطیل محاطی مربوط به هرزیر بازه را رسم می کنیم. در اینجا ارتفاع هر مستطیل برابر با طول لبه چپ آن است. بنابراین مجموع مساحت های مستطیل ها این است
. مستطیل محاطی مربوط به هرزیر بازه را رسم می کنیم. در اینجا ارتفاع هر مستطیل برابر با طول لبه چپ آن است. بنابراین مجموع مساحت های مستطیل ها این است
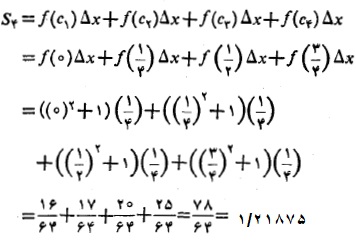
حاصل جمع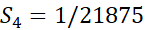 مقدار تقریبی مساحت ناحیه زیر خم
مقدار تقریبی مساحت ناحیه زیر خم
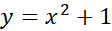 از
از است. چون مستطیل ها همه ناحیه زیرخم را نمی پوشانند، مقدار
است. چون مستطیل ها همه ناحیه زیرخم را نمی پوشانند، مقدار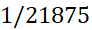 تقریبی نقصانی از مساحت است.
تقریبی نقصانی از مساحت است.
نماد مجموع
برای رعایت اختصار، غالبا مجموعه هایی نظیر
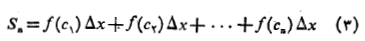
را با استفاده از حرف بزرگ یونانی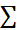 (سیگما) که مشخص کننده کلمه «مجموع» است به صورت زیر می نویسیم
(سیگما) که مشخص کننده کلمه «مجموع» است به صورت زیر می نویسیم
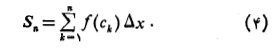
( این رابطه را چنین می خوانیم:«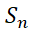 برابر است با مجموع
برابر است با مجموع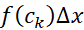 از
از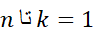 »). این نمادگذاری را نوشتن مجموع با نماد سیگما می نامند.
»). این نمادگذاری را نوشتن مجموع با نماد سیگما می نامند.
توجه کنید که هر جمله مجموع در رابطه (3) به صورت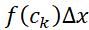 ، و تفاوت جمله ها با یکدیگر در اندیس
، و تفاوت جمله ها با یکدیگر در اندیس است.
است.
اندیس را با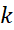 نشان داده ایم. اما از
نشان داده ایم. اما از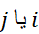 یا از هر نماد دیگری که برای چیز دیگری به کار نرود می توان استفاده کرد.
یا از هر نماد دیگری که برای چیز دیگری به کار نرود می توان استفاده کرد.
اندیس در نخستین جمله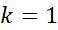 ، در دومین جمله
، در دومین جمله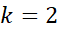 ، به همین ترتیب،...در آخرین جمله یا
، به همین ترتیب،...در آخرین جمله یا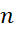 اامین جمله
اامین جمله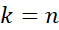 است. این مطلب رابا نوشتن
است. این مطلب رابا نوشتن 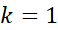 در زیر
در زیر مشخص کردیم تا روشن شود که مجموع
مشخص کردیم تا روشن شود که مجموع
با جمله ای آغاز می شود که از قرار دادن 1 به جایk در رابطه بعد از علامت سیگما به دست می آید. حرفn
در رابطه بعد از علامت سیگما به دست می آید. حرفn در بالای سیگما جای توقف را به ما نشان می دهد. مثلا اگر
در بالای سیگما جای توقف را به ما نشان می دهد. مثلا اگر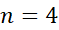 ، داریم
، داریم
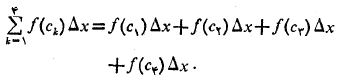
تنها تفاوت هر جمله با جمله بعدی اش مقدارk است. به جایk
است. به جایk ؛ اول1، بعد2،بعد3، و بعد4 را قرار می دهیم. سپس آن ها را جمع می کنیم.
؛ اول1، بعد2،بعد3، و بعد4 را قرار می دهیم. سپس آن ها را جمع می کنیم.
 مثال2
مثال2

مساحت ناحیه زیریک خم
فرمول های کلی مساحت مثلث، ذوزنقه و دایره را که همگی شکل هایی در هندسه کلاسیک یونانی هستند می دانیم. اما از دوران قبل از پیدایش حساب دیفرانسیل وانتگرال هیچ فرمول کلی برای مساحت ناحیه دلخواه زیر نمودار توابع نامنفی پیوسته درست نیست. اکنون باید این مساحت ها را تعریف کنیم.
این مساحت ها را به صورت حد مجموع مساحت های مستطیل های محاطی تعریف می کنیم. بر مبنای قضیه ای که بعدا بیان می کنیم این حدها همواره وجود دارند.
تعریف مساحت ناحیه زیریک خم
مساحت ناحیه زیر نمودار تابع پیوسته نامنفی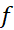 در بازه
در بازه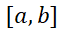 حد مجموع مساحت های مستطیل محاطی با قاعده مساوی است وقتی که تعداد مستطیل ها،
حد مجموع مساحت های مستطیل محاطی با قاعده مساوی است وقتی که تعداد مستطیل ها،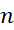 ، به سویبینهایت میل کند. با استفاده از نمادها
، به سویبینهایت میل کند. با استفاده از نمادها
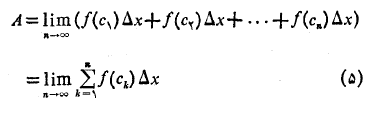
که در آن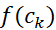 کمترین مقدار
کمترین مقدار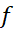 روی بازه
روی بازه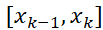 است.
است.
انتگرال ریمان
وجود حد در معادله(5) نتیجه قضیه کلیتری است که در مورد هر تابع پیوسته روی بازه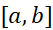 به کار می رود. در این قضیه کلیتر، تابع می تواند منفی هم باشد.
به کار می رود. در این قضیه کلیتر، تابع می تواند منفی هم باشد.
نخست قضیه را بیان می کنیم، و سپس به علت درستی آن می پردازیم. برای سهولت بررسی، از تصاویر توابع مثبت کمک می گیریم ولی مطالب کلی ای که به کمک این تصاویر تشریح می شوند برای هر تابع پیوسته دلخواهی صادق اند.
تابع مفروض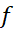 را که روی
را که روی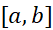 پیوسته است در نظر می گیریم. مطابق شکل نقاط زیر را بین
پیوسته است در نظر می گیریم. مطابق شکل نقاط زیر را بین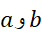 درج می کنیم.
درج می کنیم.
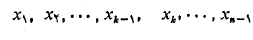
این نقاط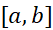 را به
را به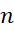 زیر بازه با طول های زیر که ضرورتی ندارد مساوی باشند، تقسیم می کنند
زیر بازه با طول های زیر که ضرورتی ندارد مساوی باشند، تقسیم می کنند
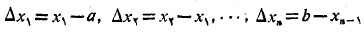
چون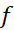 پیوسته است درهر زیر بازه یک مقدارمینیمم،
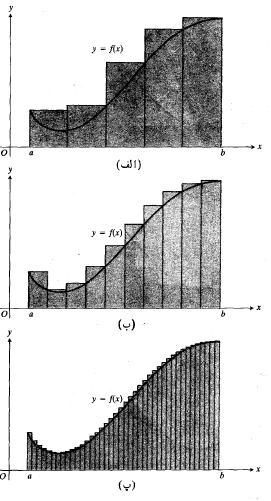
پیوسته است درهر زیر بازه یک مقدارمینیمم،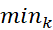 ، و یک مقدار ماکسیمم،
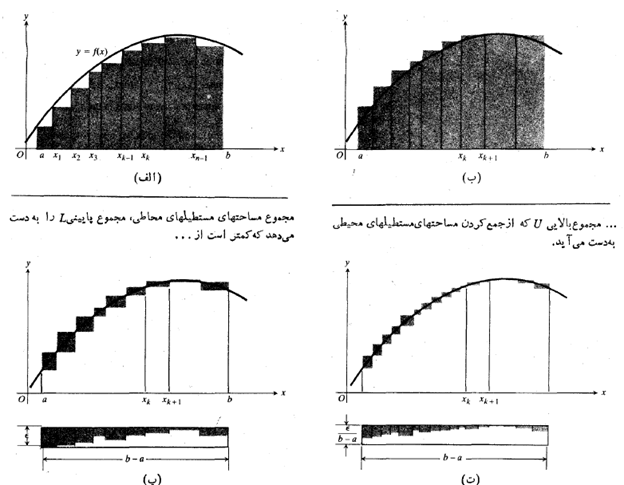
، و یک مقدار ماکسیمم،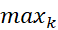 دارد. در مجموع مساحت های مستطیل های سایه دار، در قسمت (الف) شکل فوق را مجموع پایینی می نامیم. این مجموع چنین است
دارد. در مجموع مساحت های مستطیل های سایه دار، در قسمت (الف) شکل فوق را مجموع پایینی می نامیم. این مجموع چنین است
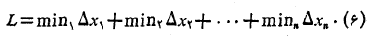
مجموع مساحت های مستطیل های سایه دار قسمت(ب) شکل فوق را مجموع بالایی می نامیم. این مجموع چنین است
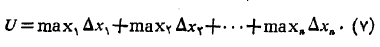
تفاضل مجموعه های بالایی و پایینی یعنی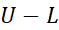 برابر مجموع مساحت های بلوک های سایه دار قسمت(پ) شکل فوق است.
برابر مجموع مساحت های بلوک های سایه دار قسمت(پ) شکل فوق است.
ایده ای که ما به دنبال آن هستیم و قسمت(پ) شکل فوق آن را القا می کند این است که هرچه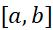 ظریف تر تقسیم شود،مساحت
ظریف تر تقسیم شود،مساحت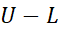 کمتر است.
کمتر است.
هدف این است که کاری کنیم که ضلع بالایی مستطیل ها تقریبا برخم منطبق شوند و در نتیجه تفاضل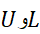 کاهش یابد. دست کم در نظر داریم تعداد
کاهش یابد. دست کم در نظر داریم تعداد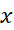 ها را افزایش دهیم تا پهنای مستطیل ها کوچکتر شود.
ها را افزایش دهیم تا پهنای مستطیل ها کوچکتر شود.
به بیان دیگر می خواهیم تقسیم را ظریف تر انجام دهیم یعنی را چنان تقسیم کنیم که چهن ترین زیربازه کوچکتر از قبل شود. بنابراین نرم تقسیم
را چنان تقسیم کنیم که چهن ترین زیربازه کوچکتر از قبل شود. بنابراین نرم تقسیم
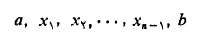
را پهنای پهن ترین زیر بازه تعریف می کنیم. بنابراین وقتی که نرم به سمت صفر میل کند تعداد زیربازه ها بیشتر و پهنای آن ها کمتر می شود. در قسمت (پ) شکل فوق با میل کردن نرم به سمت صفر، تعداد بلوک ها افزایش می یابد و پهنای آن ها کم می شود ( اما مجموع پهنای آن ها ثابت و برابر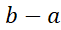 است) و هرچه پهنایشان کمتر شود کوتاهتر نیز می شوند.
است) و هرچه پهنایشان کمتر شود کوتاهتر نیز می شوند.
مطابق قسمت(ت) شکل با میل کردن نرم تقسیم بازه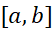 به سمت قفر تفاضل
به سمت قفر تفاضل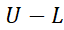 از هر
از هر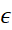 مثبت از قبل تعیین شده ای کمتر شود. به بیان دیگر
مثبت از قبل تعیین شده ای کمتر شود. به بیان دیگر
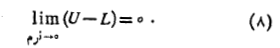
و همانگونه که در کتاب های پیشرفته اثبات می شود داریم
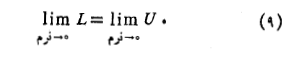
روابط(8) و (9) برای هر تابع پیوسته ای صادق است و ویژگی خاصی به اسمپیوستگی یکنواخت دارد، که توابع پیوسته در یک بازه بسته کراندار دارند. این ویژگی تضمین می کند که وقتی نرم به سمت صفر میل کند، بلوک های (پ) شکل بالا که تفاضل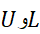 را نشان می دهند کوتاهتر و نازکتر می شوند، و م یتوانیم با نازک کردن آن ها به قدر دلخواه کوتاهشان کنیم.
را نشان می دهند کوتاهتر و نازکتر می شوند، و م یتوانیم با نازک کردن آن ها به قدر دلخواه کوتاهشان کنیم.
این استدلال در اساس درست است و تصویری صحیح از اثبات کامل به دست می دهد.
فرض می کنیم اثبات کرده ایم که رابطه (9) در مورد هرتابع پیوسته روی 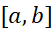 صدق می کند. درهر زیربازه
صدق می کند. درهر زیربازه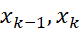 که از تقسیم بازه
که از تقسیم بازه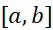 به دست می آید نقطه ای مانند
به دست می آید نقطه ای مانند در نظر می گیریم و مجموع زیر را تشکیل می دهیم
در نظر می گیریم و مجموع زیر را تشکیل می دهیم
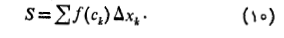
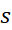 نیز مانند مجموع های
نیز مانند مجموع های
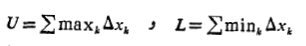
مجموعی است از حاصل ضرب مقادیر تابع در طول بازه ها. اما در اینجا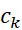 ها به طور تصادفی انتخاب شده اند و آنچه درباره مقدار
ها به طور تصادفی انتخاب شده اند و آنچه درباره مقدار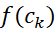 می دانیم این است که
می دانیم این است که
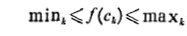
ولی دانستن همین مطلب برای به دست اوردن رابطه زیر کافی است

و بنابراین داریم
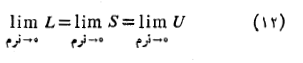
به بیان دیگر حد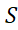 با حد
با حد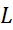 و حد
و حد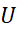 یکی است. از رابطه (12) حقیقتا به نتیجه ای قابل ملاحظه دست می یابیم. بنابارین تساوی، چگونگی انتخاب نقاط
یکی است. از رابطه (12) حقیقتا به نتیجه ای قابل ملاحظه دست می یابیم. بنابارین تساوی، چگونگی انتخاب نقاط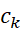 برای تشکیل مجموع
برای تشکیل مجموع
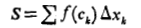
برای یک تابع پیوسته در بازه ای چون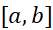 اهمیت ندارد، و اگر نرم تقسیم به سمت صفر میل کند همواره یک حد ثابت به دست می آید.
اهمیت ندارد، و اگر نرم تقسیم به سمت صفر میل کند همواره یک حد ثابت به دست می آید.
اگر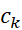 را چنان برگزینیم که
را چنان برگزینیم که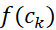 روی
روی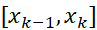 مقدار ماکسیمم
مقدار ماکسیمم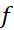 باشد، حد فرق نمی کند. می توان
باشد، حد فرق نمی کند. می توان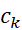 ها را تصادفی هم انتخاب کرد.
ها را تصادفی هم انتخاب کرد.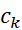 ها هرچه باشند حد فرق نمی کند.
ها هرچه باشند حد فرق نمی کند.
انتگرال ریمان به شکل زیر نشان داده می شود
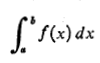
گیر انداختن حد بین مجموع های بالایی و پایینی از ایده های ریمان بود. مجموع
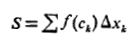
را مجموع تقریب زننده یا مجموع ریمان انتگرال می نامند. اعداد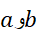 را حدود انتگرال گیری،
را حدود انتگرال گیری،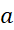 حد پایینی و
حد پایینی و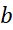 را حد بالایی آن می نامند.
را حد بالایی آن می نامند.
جهت مطالعه بیشتر مباحث فوق از محصولکپسول آموزشی ریاضی عمومی 1 از سایتلینوم استفاده کنید.