انتگرال گیری
یکی از اولین هنرهای حساب دیفرانسیل و انتگرال پیش بینی مکان آینده یک جسم متحرک به کمک مکان ان در لحظات پیشین و تابع سرعتش بود. ما امروزه به این امر به عنوان یکی از مواردی می نگریم که در آن ها توابع را از اطلاعاتی که دربازه مشتقاتشان داریم تعیین می کنیم.
ما سرعت اجسامی را که شتابان معلوم است محاسبه می کنیم. میزان جمعیت در آینده را با استفاده از جمعیت فعلی و آهنگ تغییر آن حساب می کنیم.
نظریه یافتن توابعی که مشتقاتشان معلوم اند قسمتی از حساب انتگرال است. انتگرال گرفتن از یک تابع، یافتن همه توابعی است که مشتقشان آن تابع است،یا اصطلاحا یافتن همه «پاد مشتق ها» ی تابع مفروض است. وقتی از لغت انتگرال گیری به معنی مجموع یابی استفاده می کنیم، منظورمان فرایندیریاضی است که ما را قادر می سازد مساحت ناحیه ای را که مرز خمیده دارد، حجم جسمی در فضا، نیرویی که آب پشت سد به سد وارد می کند، یا مقدار انرژی لازم برای بردن یک ماهواره به مدار را محاسبه کنیم.
انتگرال گیری نامعین
این قسمت را با یافتن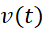 ، تابع سرعت جسمی که از حال سکون با شتاب ثابت
، تابع سرعت جسمی که از حال سکون با شتاب ثابت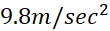 سقوط می کند آغاز می کنیم.
سقوط می کند آغاز می کنیم.
برای این منظور معادله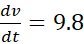 را با شرط
را با شرط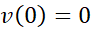 حل می کنیم. این معادله یکی از معادلات دیفرانسیلی (معادلاتی که در آن ها مشتق وجود دارد) است که با معکوس کردن فرمول های آشنایمشتق قابل حل است.
حل می کنیم. این معادله یکی از معادلات دیفرانسیلی (معادلاتی که در آن ها مشتق وجود دارد) است که با معکوس کردن فرمول های آشنایمشتق قابل حل است.
مجموعه همه پاد مشتق های یک تابع را انتگرال نامعین آن تابع می نامیم.
تعیین سرعت
شتاب گرانش در نزدیکی سطح زمین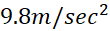 است. یعنی آهنگ تغییر سرعت
است. یعنی آهنگ تغییر سرعت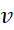 ی جسمی که در نزدیکی سطح زمین و خلاء سقوط آزاد می کند برابر است با
ی جسمی که در نزدیکی سطح زمین و خلاء سقوط آزاد می کند برابر است با

اگر جسم از حال سکون رها شود، سرعت آن پس از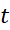 ثانیه چقدر است؟
ثانیه چقدر است؟
برای تعیین سرعت،
 ، باید از تنها دو مطلبی که دربازه
، باید از تنها دو مطلبی که دربازه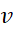
 به صورت تابعی از
به صورت تابعی از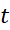 می دانیم بهره بگیریم. یعنی اینکه
می دانیم بهره بگیریم. یعنی اینکه

کار را با معادله شتاب شروع می کنیم و می پرسیم«چه توابعی از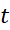 مشتقشان دقیقا برابر با 9.8 است؟ » یکی از این توابع، بنا به تجربه، این است
مشتقشان دقیقا برابر با 9.8 است؟ » یکی از این توابع، بنا به تجربه، این است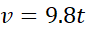
اما جواب های دیگری نیز وجود دارند، زیرا

به ازای هر مقداری از ثابت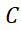 یک جواب است. سرعت یک جسم در حال سقوط از رابطه زیر به ازای مقدار مشخصی از
یک جواب است. سرعت یک جسم در حال سقوط از رابطه زیر به ازای مقدار مشخصی از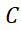 به دست می آید
به دست می آید

این سوال مطرح می شود که این مقدار مشخص 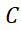
 در این مسئله خاص کدام است؟ برای پاسخ دادن به این سوال،
در این مسئله خاص کدام است؟ برای پاسخ دادن به این سوال،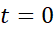 را در معادله (3) قرار می دهیم و با استفاده از این واقعیت که
را در معادله (3) قرار می دهیم و با استفاده از این واقعیت که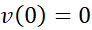 ، چنین به دست می آوریم
، چنین به دست می آوریم
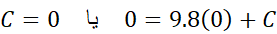
بنابراین ، سرعت جسم در حال سقوط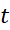
 ثانیه پس از رها شدن چنین است
ثانیه پس از رها شدن چنین است

معادله های دیفرانسیل
از نظر ریاضی، مساله تعیین سرعت یک جسم در حال سقوطاز روی شتابش حالت خاصی است از تعیین یک تابع 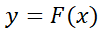 گه مشتقش را معادله زیر روی بازه ای از مقادیر
گه مشتقش را معادله زیر روی بازه ای از مقادیر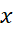
 به دست می دهد.
به دست می دهد.

معادله ای نظیرمعادله (5) را که در آن مشتق وجود دارد معادله دیفرانسیل می نامند.
معادله(5)،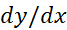 را به صورت تابعی از
را به صورت تابعی از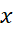
 به دست می دهد. در یک معادله دیفرانسیل پیچیده تر مانند معادله زیر،
به دست می دهد. در یک معادله دیفرانسیل پیچیده تر مانند معادله زیر،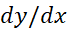 می تواند تابعی از
می تواند تابعی از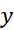
 هم باشد
هم باشد
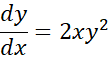
معادله دیفرانسیل می تواند شامل مشتقات مراتب بالاتر هم باشد
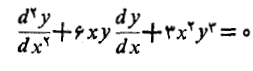
اما فعلا تنها به معادلاتی می پردازیم که شامل یک تک مشتق مرتبه اول اند. تابع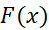 را یک جواب معادله دیفرانسیل
را یک جواب معادله دیفرانسیل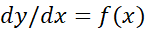 روی بازه
روی بازه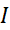
 می نامیم هرگاه نقطه
می نامیم هرگاه نقطه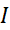 مشتق پذیر باشد و درهر نقطه از
مشتق پذیر باشد و درهر نقطه از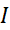
 داشته باشیم
داشته باشیم
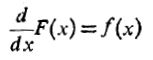
تابع را یک پاد مشتق
را یک پاد مشتق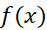 نیز می نامند.
نیز می نامند.
حل کردن معادله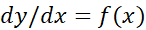 در بازه
در بازه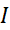 به معنی یافتن همه توابعی است که روی
به معنی یافتن همه توابعی است که روی تعریف بشوند و پاد مشتق
تعریف بشوند و پاد مشتق باشند. بازه می تواند متناهی یا نامتناهی باشد.
باشند. بازه می تواند متناهی یا نامتناهی باشد.
انتگرال نامعین
اگر تابع پاد مشتق
پاد مشتق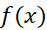 باشد، آنگاه
باشد، آنگاه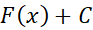 به ازای هر مقدار ثابت
به ازای هر مقدار ثابت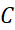
 یک پاد مشتق
یک پاد مشتق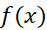 است زیرا اگر
است زیرا اگر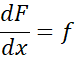 ، آنگاه
، آنگاه
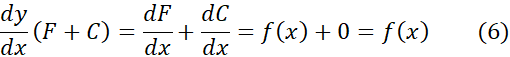
آیا جز پاد مشتق هایی که فرمول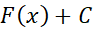 به به دست می دهد،
به به دست می دهد،
 پاد مشتق دیگری هم دارد؟ نتیجه 3ی قضیه مقدار میانگین چنین بیان می کند:«خیر. هر پاد مشتق
پاد مشتق دیگری هم دارد؟ نتیجه 3ی قضیه مقدار میانگین چنین بیان می کند:«خیر. هر پاد مشتق
 از این فرمول به ازای مقدار خاصی از
از این فرمول به ازای مقدار خاصی از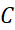 به دست می آید». بنابراین اگر
به دست می آید». بنابراین اگر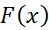 جوابی برای
جوابی برای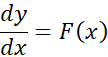 باشد، فرمول
باشد، فرمول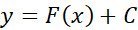 همه جواب را به دست می دهد.
همه جواب را به دست می دهد.
مجموعه همه پاد مشتق های یک تابع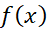 را انتگرال نامعین
را انتگرال نامعین نسبت به
نسبت به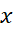
 می نامند. نماد انتگرال نامعین چنین است
می نامند. نماد انتگرال نامعین چنین است
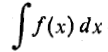
هرگاه فرمول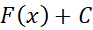 همه پاد مشتق های
همه پاد مشتق های
 را به دست دهد، آن را چنین مشخص می کنیم
را به دست دهد، آن را چنین مشخص می کنیم
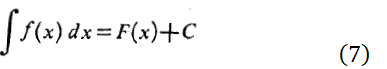
این معادله را به دو صورت می توان خواند:«انتگرال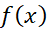 نسبت به
نسبت به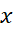
 برابر است با
برابر است با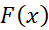 به علاوه
به علاوه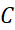
 » یا «انتگرال
» یا «انتگرال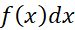 برابر است با
برابر است با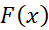 به علاوه
به علاوه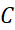 ».نماد∫ علامت انتگرال است. تابع
».نماد∫ علامت انتگرال است. تابع
 انتگرالده انتگرال، و
انتگرالده انتگرال، و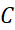
 ثابت انتگرال گیری است.
ثابت انتگرال گیری است.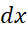 نشان می دهد که متغیر انتگرالگیری
نشان می دهد که متغیر انتگرالگیری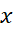 است.
است.
در مثال جسم در حال سقوط ، دریافتیم که انتگرال9.8 نسبت به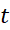
 برابر است با
برابر است با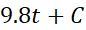 :
:

در اینجا انتگرالده،تابع ثابت 9.8 و متغیر انتگرال گیری،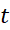
 است.
است.
 مثال 1 معادله دیفرانسیل زیر را حل کنید
مثال 1 معادله دیفرانسیل زیر را حل کنید
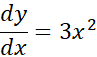
حل:بنا به تجربه می دانیم که
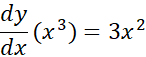
بنابراین
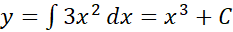
جدا کردن متغیرها
اگر در یک معادله دیفرانسیل،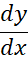 هم بر حسب
هم بر حسب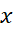
 و هم بر حسب
و هم بر حسب بیان شود، معادله ای داریم که یک متغیر را صریحا بر حسب دیگری به دست نمی دهد. حل معادله دیفرانسیل
بیان شود، معادله ای داریم که یک متغیر را صریحا بر حسب دیگری به دست نمی دهد. حل معادله دیفرانسیل

به معنی یک تابع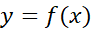 است کهمشتق آن،
است کهمشتق آن،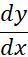 ، درهر
، درهر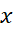
 خاصی مساوی
خاصی مساوی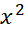 برابر مقدار
برابر مقدار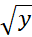 در
در
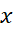 باشد. روشی که گاه به کار می رود چنین است که همه جملات شامل
باشد. روشی که گاه به کار می رود چنین است که همه جملات شامل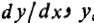 را به یک طرف معادله و همه جملات شامل
را به یک طرف معادله و همه جملات شامل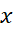
 را به طرف دیگر ببریم. این روش را جدا کردن متغیرهامی نامیم.
را به طرف دیگر ببریم. این روش را جدا کردن متغیرهامی نامیم.
اگر بتوانیم متغیرها را جدا کنیم، چنانکه در مثال زیر دیده می شود، می توانیم
 را با انتگرال گیری تعیین کنیم.
را با انتگرال گیری تعیین کنیم.
 مثال 2 معادله دیفرانسیل زیر را حل کنید.
مثال 2 معادله دیفرانسیل زیر را حل کنید.

حل: برای جدا کردن متغیرها طرفین معادله را بر 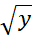 تقسیم می کنیم
تقسیم می کنیم

با این فرض که معادله اصلی را به صورت تابعی مشتق پذیر از
را به صورت تابعی مشتق پذیر از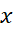 تعریف می کند، می بینیم که طرف چپ معادله(9)مشتق تابع
تعریف می کند، می بینیم که طرف چپ معادله(9)مشتق تابع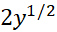 نسبت به
نسبت به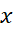
 است.
است.
طرف راست مشتق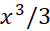 نسبت به
نسبت به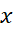 است. بنابراین با انتگرال گیری از دو طرف معادله(9) نسبت به
است. بنابراین با انتگرال گیری از دو طرف معادله(9) نسبت به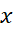 داریم
داریم
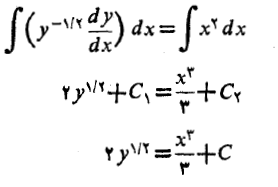
که در آن 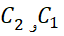 ادغام شده و به صورت یک ثابت
ادغام شده و به صورت یک ثابت 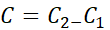 در آمده اند. هرگاه بتوان دسته ای جواب را با یک ثابت توصیف کرد نیازی به توصیف آن با دو ثابت نیست،زیرا با استفاده از دو ثابت به انتگرال های نامعین کلیت بیشتری بخشیده نمی شود.
در آمده اند. هرگاه بتوان دسته ای جواب را با یک ثابت توصیف کرد نیازی به توصیف آن با دو ثابت نیست،زیرا با استفاده از دو ثابت به انتگرال های نامعین کلیت بیشتری بخشیده نمی شود.
فرمول های انتگرال گیری
به کمک فرمول هایی در بسیاری از موارد می توان کمتر به حدس تکیه کرد. در این فرمول ها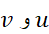 توابعمشتق پذیر از
توابعمشتق پذیر از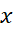 اند،
اند،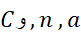 ثابت اند.
ثابت اند.
شرح این فرمول ها چنین است:
1.انتگرال مشتق یک تابع مشتق پذیر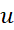 برابر است با
برابر است با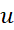
 به علاوه یک ثابت دلخواه.
به علاوه یک ثابت دلخواه.
2.یک ثابت را می توان از زیر نماد انتگرال گیری بیرون آورد. ( توجه: عباراتی را که توابعی از متغیرانتگرال گیری اند نمی توان از زیرنماد انتگرال گیری بیرون آورد.)
3.انتگرال مجموع دو تابع برابر مجموع انتگرال های آن ها است. این مطلب را می توان به مجموع هر تعداد متناهی از توابع تعمیم داد.
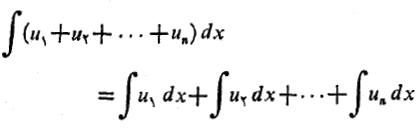
4.اگر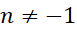 ، انتگرال
، انتگرال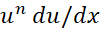 با افزودن 1 به نما، تقسیم نتیجه بر نمای جدید،و افزودن یک ثابت دلخواه به حاصل به دست می آید.
با افزودن 1 به نما، تقسیم نتیجه بر نمای جدید،و افزودن یک ثابت دلخواه به حاصل به دست می آید.
فرمول (1) بیان دیگری است از تعریف انتگرال نامعین به عنوان مجموعه همه توابع دارای یکمشتق مفروض.
این فرمول حاکی است که هر تابعی که مشتقش 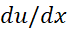 باشد باید با فرمول
باشد باید با فرمول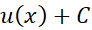 ، به ازای مقدار خاصی از
، به ازای مقدار خاصی از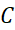
 ، مشخص شود. با چند مثال چگونگی استفاده از این فرمول ها را در به دست آوردن انتگرال های نامعین نشان می دهیم.
، مشخص شود. با چند مثال چگونگی استفاده از این فرمول ها را در به دست آوردن انتگرال های نامعین نشان می دهیم.
فرمول های انتگرال گیری
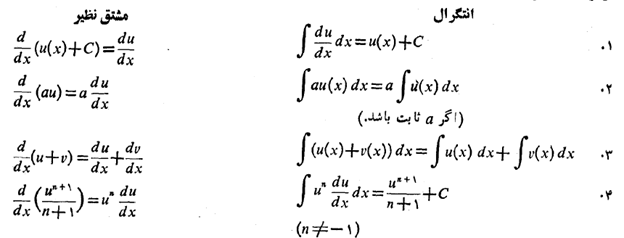
 مثال 3
مثال 3
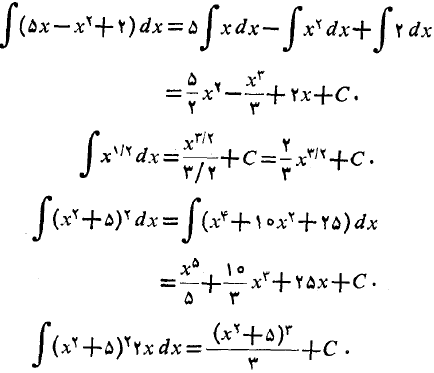
برای به دست آوردن انتگرال رابطه آخر، فرمول
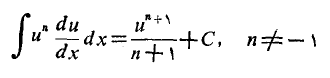
را به ازای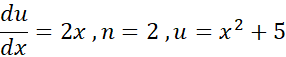 به کار برده ایم.
به کار برده ایم.
 مثال 4 تعدیل انتگرالده به کمک یک ثابت. انتگرال زیر را حساب کنید.
مثال 4 تعدیل انتگرالده به کمک یک ثابت. انتگرال زیر را حساب کنید.
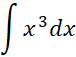
حل: می دانیم که
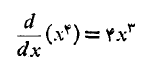
بنابراین
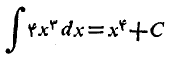
از این رو انتگرال مطلوب را می توان چنین حساب کرد: انتگرالده را به صورت زیر می نویسیم
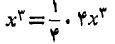
و¼ را از زیر نماد انتگرال بیرون می آوریم
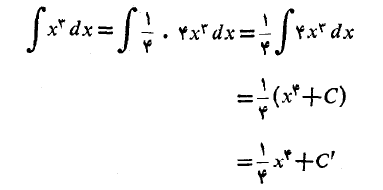
که در آن 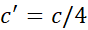

خط مشی اسلوبمند حدس و بررسی
برای به دست آوردن انتگرال تابع مفروضی که نمی توان بی درنگانتگرال آن را حساب کرد روندی وجود دارد. برای استفاده از این روند باید تجربه کافی داشته باشیم تا درباره پاسخ حدس مناسبی بزنیم اما ضرورتی ندارد حدسمان در وهله نخست درست باشد.
مراحل این روند چنین اند:
1.حدس زدن یک پاسخ مناسب
2.مقایسه مشتق این پاسخ با انتگرالده
3.تصحیح این پاسخ حدسی
4.بررسی نتیجه و انجام تصحیحات در صورت نیاز
5. افزودن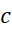
 .
.
 مثال 5 انتگرال زیر را حساب کنید
مثال 5 انتگرال زیر را حساب کنید
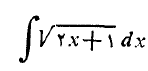
حل: تابعی را می جوییم که مشتقش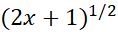 باشد. نمای این مشتق را با 1 جمع می کنیم و
باشد. نمای این مشتق را با 1 جمع می کنیم و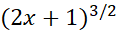 را می آزماییم. مشتق
را می آزماییم. مشتق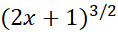 چنین است
چنین است
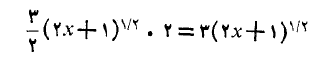
فرق این با انتگرالده در ضریب 3 است. یعنی تابع حدسی ما 3 برابر بزرگتر است. این تابع را بر 3 تقسیم می کنیم و تابع حدسی جدید زیر را به دست می آوریم
در ضریب 3 است. یعنی تابع حدسی ما 3 برابر بزرگتر است. این تابع را بر 3 تقسیم می کنیم و تابع حدسی جدید زیر را به دست می آوریم
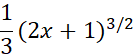
مشتق این تابع جدید چنین است
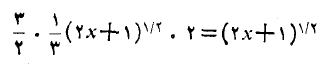
و این همان تابعی است که ما انتگرالش را می جستیم. پس
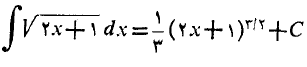
انتخاب مقدار ثابت انتگرال گیری
در حل یک معادله دیفرانسیل مانند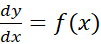 معمولا به دنبال جواب خاصی هستیم که شرایط عددی از پیش تعیین شده را برآورده سازد.
معمولا به دنبال جواب خاصی هستیم که شرایط عددی از پیش تعیین شده را برآورده سازد.
بدین منظور نخست جواب عمومی،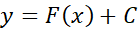 ، را تعیین می کنیم که همه جواب های ممکن را به دست می دهد. سپس مقداری از
، را تعیین می کنیم که همه جواب های ممکن را به دست می دهد. سپس مقداری از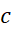 را تعیین می کنیم که جواب خاص مطلوب را به دست دهد.
را تعیین می کنیم که جواب خاص مطلوب را به دست دهد.
همه نمودارهای خم های جواب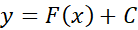 از انتقال خم جواب
از انتقال خم جواب 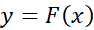 به اندازه
به اندازه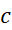
 در امتداد قائم به دست می آید. بنابراین، این نمودارها دسته ای از خم های«موازی» تشکیل می دهند و کنار هم قرار می گیرند و صفحه بالا و پایین دامنه
در امتداد قائم به دست می آید. بنابراین، این نمودارها دسته ای از خم های«موازی» تشکیل می دهند و کنار هم قرار می گیرند و صفحه بالا و پایین دامنه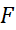
 را پر می کنند.
را پر می کنند.
با نگاهی به شکل زیر متوجه موضوع خواهید شد. در این شکل چند تا از خم های تشکیل دهنده جواب عمومی معادله 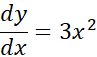 ، یعنی
، یعنی 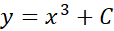 رسم شده است.
رسم شده است.
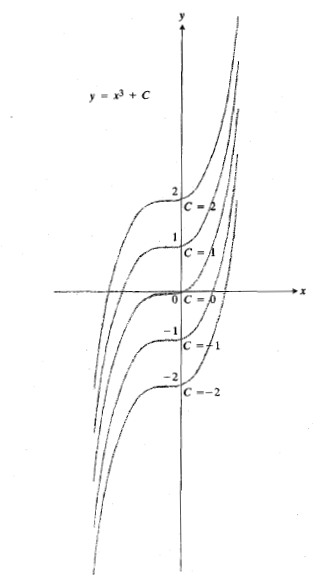
اگر نقطه ای چون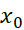 از دامنه
از دامنه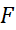 را درنظر بگیریم و مقدار دلخواه
را درنظر بگیریم و مقدار دلخواه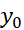 را برگزینیم، می توان با قرار دادن
را برگزینیم، می توان با قرار دادن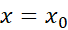 و
و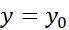 در معادله
در معادله
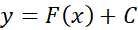 و حل آن نسبت به
و حل آن نسبت به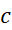 جوابی را یافت که از نقطه
جوابی را یافت که از نقطه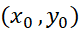 بگذرد. به این ترتیب داریم
بگذرد. به این ترتیب داریم
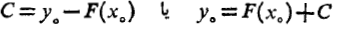
خم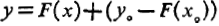 خمی است که از
خمی است که از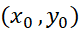 می گذرد.
می گذرد.
این شرط که «وقتی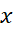 برابر با
برابر با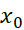 است
است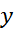 برابر با
برابر با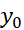 است.» یک شرط اول نام دارد. این نامگذاری از مسائلی ناشی می شود که در آن ها زمان، متغیر مستقل و
است.» یک شرط اول نام دارد. این نامگذاری از مسائلی ناشی می شود که در آن ها زمان، متغیر مستقل و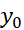 سرعت یا مکان جسم متحرک در زمان اولیه
سرعت یا مکان جسم متحرک در زمان اولیه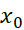 است.
است.
تا اینجا دریافتیم که همواره می توان از جواب عمومی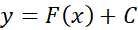 جواب خاصی را برگزید که در شرط اولیه مفروضی، مشروط به اینکه
جواب خاصی را برگزید که در شرط اولیه مفروضی، مشروط به اینکه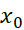 در دامنه
در دامنه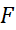
 باشد، صدق کند.
باشد، صدق کند.
 مثال 1 با توجه به شکل قسمت قبل خمی بیابید که شیب ان در نقطه
مثال 1 با توجه به شکل قسمت قبل خمی بیابید که شیب ان در نقطه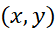 برابر
برابر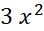 باشد و از نقطه
باشد و از نقطه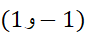 بگذرد.
بگذرد.
حل: به زبان ریاضی، مطلوب ما حل مساله ای است که با مشخصات زیر
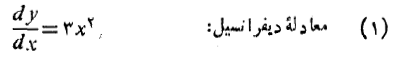
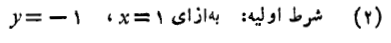
نخست با انتگرال گیری از طرفین معادله دیفرانسیل نسبت به جواب عمومی آن را می یابیم.
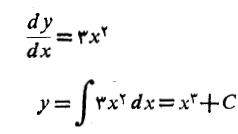
سپس برای تعیین جواب خاصی که نمودارش از نقطه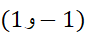 بگذارد، مقداری از
بگذارد، مقداری از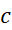
 را می یابیم که به ازای آن وقتی
را می یابیم که به ازای آن وقتی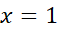 داشته باشیم
داشته باشیم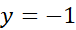 .
.
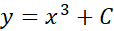
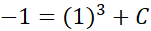
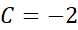
بنابراین جواب مطلوب 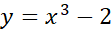 است. شیب خم،
است. شیب خم، 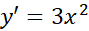 است و خم از نقطه
است و خم از نقطه 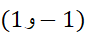 می گذارد.
می گذارد.
 مثال 2 سرعت جسم متحرکی در لحظه
مثال 2 سرعت جسم متحرکی در لحظه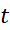
 چنین است
چنین است
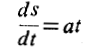
که در آنa ثابت و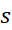 مکان جسم در لحظه
مکان جسم در لحظه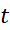
 است. اگر به ازای
است. اگر به ازای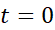 داشته باشیم
داشته باشیم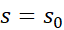 ، تابع
، تابع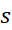 بر حسب
بر حسب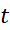 را بیابید.
را بیابید.
حل: مطلوب ما حل مساله ای است با این مشخصات:
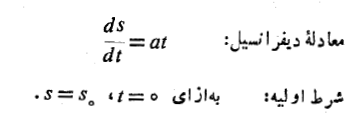
با انتگرال گیری از طرفین معادله دیفرانسیل نسبت به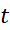 ، جواب عمومی آن را می یابیم
، جواب عمومی آن را می یابیم
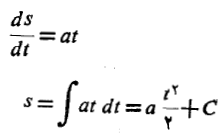
سپس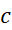
 را چنان می یابیم که جواب خاص،برآورنده شرط
را چنان می یابیم که جواب خاص،برآورنده شرط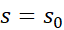 و
و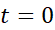 باشد. برای انجام این کار
باشد. برای انجام این کار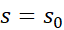 و
و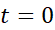 را در فرمول جواب عمومی قرار می دهیم و
را در فرمول جواب عمومی قرار می دهیم و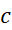 را محاسبه می کنیم.
را محاسبه می کنیم.
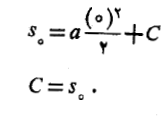
جواب مطلوب چنین است
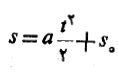
 مثال 3 پرتابه ای از یک سکو که در ارتفاع 10 فوتی از سطح زمین قرار دارد در امتداد قائم به طرف بالا پرتاب می شود. سرعت اولیه160 ft/sec است.
مثال 3 پرتابه ای از یک سکو که در ارتفاع 10 فوتی از سطح زمین قرار دارد در امتداد قائم به طرف بالا پرتاب می شود. سرعت اولیه160 ft/sec است.
بنابه فرض، تنها نیروی موثر برحرکت پرتابه در ضمن حرکتش نیروی گرانش است که به اندازه 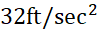 شتاب به طرف پایین ایجاد می کند. به فرض اینکه در لحظه پرتاب
شتاب به طرف پایین ایجاد می کند. به فرض اینکه در لحظه پرتاب 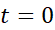 باشد معادله ای برای ارتفاع پرتابه از سطح زمین، به صورت تابعی از
باشد معادله ای برای ارتفاع پرتابه از سطح زمین، به صورت تابعی از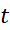
 بیابید.
بیابید.
حل: اگر ارتفاع پرتابه از سطح زمین را با
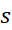 نشان دهیم، سرعت و شتاب پرتابه چنین اند
نشان دهیم، سرعت و شتاب پرتابه چنین اند
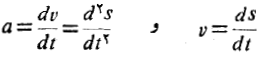
چون پرتابه به طرف بالا پرتاب، و نیروی گرانش در جهت مخالف بر آن وارد می شود سرعت، تابعی نزولی از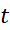
 است. بنابراین معادله دیفرانسیلی که باید حل شود معادله
است. بنابراین معادله دیفرانسیلی که باید حل شود معادله
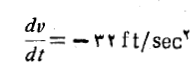
با شرط اولیه زیر است
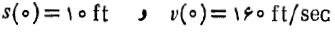
پس از یک بارانتگرال گیری داریم
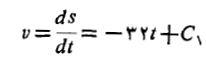
اگر از این معادله دوباره انتگرال بگیریم چنین به دست می آید
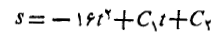
مقادیر مناسب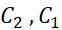 از شرایط اولیه چنین به دست می آیند
از شرایط اولیه چنین به دست می آیند
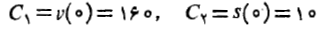
پس معادله حرکت چنین است
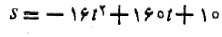
برای مطالعه مباحث پیشرفته و بیشتر درسایت لینوم ازمحصول کپسول ریاضی 1 استفاده کنید.