کاربرد انتگرال معین
اهمیت حساب انتگرال از این واقعیت ناشی می شود که بسیاری از چیزهایی را که مایلیم بدانیم می توانیم با انتگرال محاسبه کنیم. مساحت رویه های محدود به خم ها، حجم اجسام سه بعدی، طول خم ها، مساحت رویه های خمیده، گشتاورهای لختی، جذر میانگین مربع ولتاژ، نیروهای وارد بر سدها نمونه هایی هستند که همگی را می توان به طور طبیعی به عنوان حد مجموعه های متناهی تعریف کرد.
هریک از این مجموع ها، مجموع ریمانی تابعی پیوسته است که فرمولش از متنی که در آن محاسبه انجام می شود معلوم می گردد. بنابراین حد هریک از این مجموعه ها وجود دارد و می توان آن را با استفاده از قضیه محاسبه انتگرال به صورت انتگرال معین محاسبه کرد.

تغییر خالص مکان و مسافتی که یک جسم متحرک می پیماید.
برای تعیین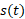 ، تغییر خالص مکان جسمی که روی یک خط از لحظه
، تغییر خالص مکان جسمی که روی یک خط از لحظه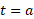 تا لحظه
تا لحظه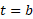 حرکت می کند، از تابع سرعت جسم،
حرکت می کند، از تابع سرعت جسم،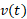 ، از
، از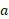 تا
تا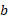 انتگرالمی گیریم.
انتگرالمی گیریم.
برای یافتن کل مسافت پیموده شده توسط جسمی که روی یک خط به عقب و جلو حرکتمی کند به عوض سرعت جسم،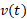 ، از مقدار سرعت، |
، از مقدار سرعت، |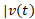 ، انتگرال می گیریم. این مقاله علت درستی این کار و روش انجام محاسبات را نشان می دهد.
، انتگرال می گیریم. این مقاله علت درستی این کار و روش انجام محاسبات را نشان می دهد.
تغییر خالص مکان
اگر جسمی روی خطی حرکت کند و سرعتش،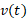 ، تابعی پیوسته از زمان باشد،به کمک انتگرال گیری می توان تابع مکان جسم را که شامل یک ثابت نامشحص
، تابعی پیوسته از زمان باشد،به کمک انتگرال گیری می توان تابع مکان جسم را که شامل یک ثابت نامشحص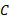 است به دست آورد.
است به دست آورد.
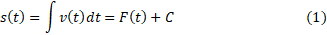
که در آن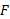 پاد مشتقی از
پاد مشتقی از است. برای یافتن تغییر خالص مکان جسم در هر فاصله زمانی خاص از
است. برای یافتن تغییر خالص مکان جسم در هر فاصله زمانی خاص از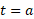 تا
تا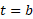 ،
،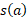 را از
را از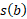 کم می کنیم
کم می کنیم
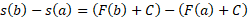
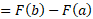
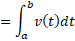
بنابراین تغییر خالص مکان جسم برابر است باانتگرالسرعت جسم از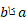 .
.
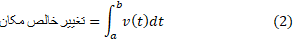
در فیزیک تغییر خالص مکان را جابجایی می نامند.
 مثال1 سرعت جسمی که روی یک خط حرکت می کند چنین است
مثال1 سرعت جسمی که روی یک خط حرکت می کند چنین است
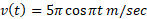
تغییر خالص مکان جسم را از لحظه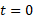 تا لحظه
تا لحظه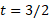 بیابید.
بیابید.
حل: بنا به تساوی (2) تغییر خالص چنین است
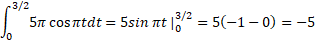
بنابراین حاصل حرکت جسم از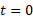 تا
تا 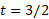 ، 5 متر جابجایی آن به سمت چپ است. مانند شکل
، 5 متر جابجایی آن به سمت چپ است. مانند شکل
توجه کنید که برای حل مثال 1 ضرورتی نداشت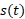 را تعیین کنیم. این بی نیازی به یافتن
را تعیین کنیم. این بی نیازی به یافتن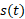 جالب است زیرا براساس اظلاعات مفروض تنها می توانیم بگوییم به ازای مقدار خاصی از
جالب است زیرا براساس اظلاعات مفروض تنها می توانیم بگوییم به ازای مقدار خاصی از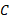 داریم
داریم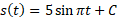 .
.
برای تعیین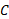 باید
باید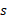 را به ازای مقدار خاصی از
را به ازای مقدار خاصی از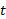 بدانیم. البته ندانستن مقدار
بدانیم. البته ندانستن مقدار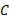 اشکالی در محاسبه تغییر خالص
اشکالی در محاسبه تغییر خالص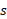 از
از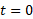 تا
تا 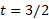 به وجود نمی آورد، زیرا
به وجود نمی آورد، زیرا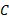 ضمن محاسبات حذف می شود
ضمن محاسبات حذف می شود
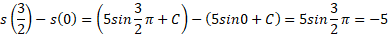
بنابراین حتی اگر دقیقا ندانیم که ذره در کجا قرار دارد، فرمول انتگرال در تساوی(2) تغییر خالص مکان ذره را به دست می دهد.
مسافت پیموده شده
اگر جهت حرکت جسمی ضمن حرکتش روی یک خط عوض شود، تغییر خالص مکان جسم از کل مسافتی که می پیماید کمتر خواهد شد. مثلا اگر جسمی از مکان اولیه اش 5 متر به طرف جلو و سپس 5 متر به طرف عقب حرکت کند، تغییر خالص مکانش صفر است در حالی که مسافتی را که می پیماید 10 متر است.
برای محاسبه کل مسافت پیموده شده به کمک انتگرال باید به گونه ای عمل کنیم که مسافات پیموده شده در حرکت به جلو و عقب همدیگر را خنثی نکنند. بدین منظور از قدر مطلقسرعت ازbتاa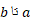 انتگرال می گیریم.
انتگرال می گیریم.
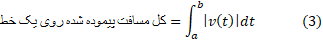
 مثال2 سرعت جسمی که روی یک خط حرکت می کند چنین است
مثال2 سرعت جسمی که روی یک خط حرکت می کند چنین است
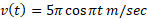
کل مسافتی را که جسم از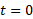 تا
تا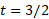 بیابید.
بیابید.
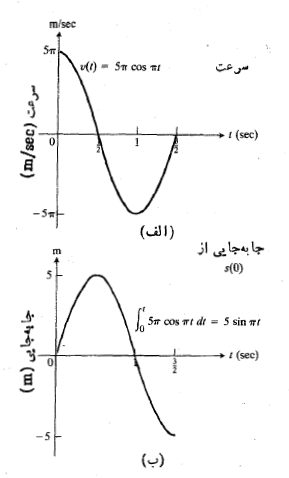
حل: نمودار را رسم می کنیم تا محل تغییر علامت مشخص شود شکل بالا قسمت (الف). بنا به تساوب(3) داریم
را رسم می کنیم تا محل تغییر علامت مشخص شود شکل بالا قسمت (الف). بنا به تساوب(3) داریم
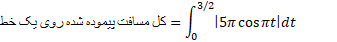
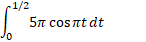
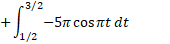
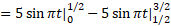
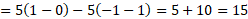
جسم ضمن حرکت 5 متر به طرف جلو و 10 متر به طرف عقب می رود و در مجموع 15 متر می پیماید. چنان که در مثال 1 دیدیم تغییر خالص مکان جسم 5 متر جابجایی به طرف چپ است.
مساحت نواحی بین خم ها
فرض می کنیم روی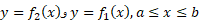 پیوسته اند و داریم
پیوسته اند و داریم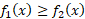 . به این ترتیب مطابق شکل از
. به این ترتیب مطابق شکل از 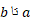 نمودار
نمودار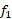 بالای نمودار
بالای نمودار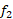 قرار می گیرد. مساحت ناحیه محدود به دو نمودار و خطوط قائم
قرار می گیرد. مساحت ناحیه محدود به دو نمودار و خطوط قائم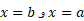 را به طریق زیر تعریف می کنیم.
را به طریق زیر تعریف می کنیم.
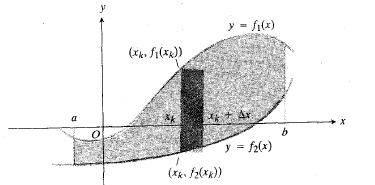
نخست بازهa≤x≤b را به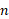 زیر بازه به طول
زیر بازه به طول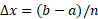 تقسیم می کنیم. بدین منظور مانند کاری که در تعریفمجموعه های ریمان کردیم، روی بازه نقاط
تقسیم می کنیم. بدین منظور مانند کاری که در تعریفمجموعه های ریمان کردیم، روی بازه نقاط 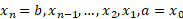 را مشخص می کنیم. سپس ناحیه بین خم ها را با مستطیل های قائم که از یک خم تا خم دیگر امتداد دارند تقریب می زنیم.
را مشخص می کنیم. سپس ناحیه بین خم ها را با مستطیل های قائم که از یک خم تا خم دیگر امتداد دارند تقریب می زنیم.
مطابق شکل بالا برای هرزیر بازه یک مستطیل در نظر می گیریم. مساحت یک مستطیل نمونه چنین است.
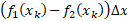
مجموع مساحت های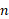 مستطیل چنین است
مستطیل چنین است
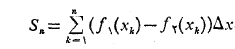
وقتی که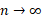 ، مجموع
، مجموع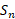 به موجب قضیه وجود انتگرال به حد زیر می گراید
به موجب قضیه وجود انتگرال به حد زیر می گراید
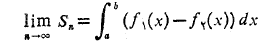
این حد مقداری است که ما آن را مساحت ناحیه بین خم ها از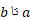 تعریف می کنیم.
تعریف می کنیم.
تعریف مساحت ناحیه بین دو خم

اگر در سراسر بازه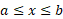 داشته باشیم
داشته باشیم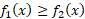 ، مساحت ناحیه بین نمودار های
، مساحت ناحیه بین نمودار های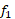 و
و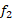 از
از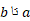 برابر است با انتگرال
برابر است با انتگرال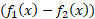 از
از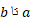 .
.
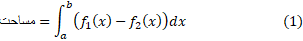
راهی برای به خاطر سپردن فرمول (1) این است که فکر کنیم مساحت نوارهای قائم،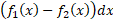 ، را در امتداد محور
، را در امتداد محور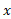 از
از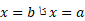 ، به کمک انتگرال جمع می کنیم. در این نماد، دیفرانسیل
، به کمک انتگرال جمع می کنیم. در این نماد، دیفرانسیل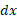 نقش دو گانه ای ایفا می کند، یعنی هم پهنای نوار مستطیلی و هم متغیر انتگرال گیری در انتگرال را نشان می دهد.
نقش دو گانه ای ایفا می کند، یعنی هم پهنای نوار مستطیلی و هم متغیر انتگرال گیری در انتگرال را نشان می دهد.
 مثال1 مساحت ناحیه ای را که از بالا به سهمی
مثال1 مساحت ناحیه ای را که از بالا به سهمی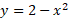 و از پایین به خط
و از پایین به خط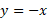 محدود است بیابید.
محدود است بیابید.
حل: برای یافتن مساحت، باید نقاط شروع و پایان ناحیه را تعیین می کنیم. بنابراین سهمی و خط را با هم رسم می کنیم مانند شکل.
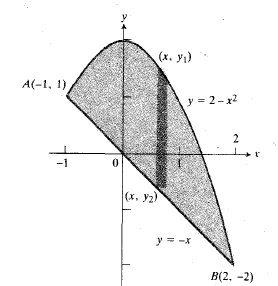
حدود انتگرال گیری انتگرال مساحت در تساوی(1) مختصهای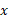 نقاط تقاطع سهمی و خط اند. این مختصها را از حل دستگاه معادلات
نقاط تقاطع سهمی و خط اند. این مختصها را از حل دستگاه معادلات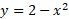 و
و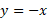 نسبت به
نسبت به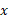 به دست می آوریم
به دست می آوریم
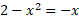
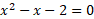
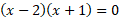
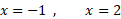
حدود انتگرال گیری 1- و 2 هستند.
به ازای همه مقادیر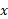 بین 1- و 2، سهمی
بین 1- و 2، سهمی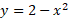 بالای خط
بالای خط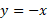 قرار دارد. بنابراین در تساوی(1) باید
قرار دارد. بنابراین در تساوی(1) باید 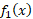 را برابر
را برابر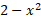 و
و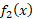 را برابر
را برابر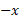 اختیار کنیم.
اختیار کنیم.
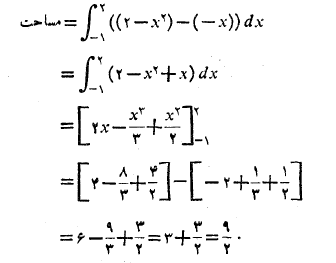
گاه چنانکه در مثال بعد خواهیم دید برای یافتن یک مساحت آسان تر است که به عوضانتگرال گیری از مساحت نوارهای قائم روی بازه ای واقع بر محور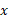 ، از نوارهای افقی روی بازه ای واقع بر محور
، از نوارهای افقی روی بازه ای واقع بر محور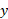 انتگرال بگیریم.
انتگرال بگیریم.
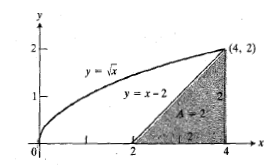
 مثال 2 مساحت ناحیه ای را بیابید که از طرف راست به خط
مثال 2 مساحت ناحیه ای را بیابید که از طرف راست به خط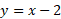 ، از طرف چپ به سهمی
، از طرف چپ به سهمی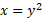 ، و از پایین به محور
، و از پایین به محور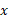 محدود است.
محدود است.
حل: روش یک انتگرال گیری نسبت به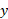 . شکل ناحیه را رسم می کنیم.
. شکل ناحیه را رسم می کنیم.
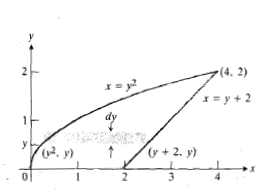
مختص های نقاط تقاطع سهمی و خط ر می توان از حل دستگاه معادلات
نقاط تقاطع سهمی و خط ر می توان از حل دستگاه معادلات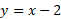 و
و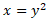 نسبت به
نسبت به 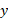 به دست آورد. با قرار دادن معادله و
به دست آورد. با قرار دادن معادله و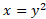 در
در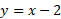 چنین به دست می آید.
چنین به دست می آید.
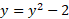
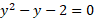
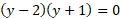
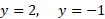
از این دو جواب تنها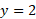 ، نقطه (4،2) یعنی نقطه تقاطع واقع در ربع اول را که ناحیه در آن قرار دارد، به دست می دهد. حال یک نوار افقی نازک را در نظر می گیریم که از سهمی واقع در طرف چپ ناحیه تا خط واقع در طرف راست آن کشیده شده است.
، نقطه (4،2) یعنی نقطه تقاطع واقع در ربع اول را که ناحیه در آن قرار دارد، به دست می دهد. حال یک نوار افقی نازک را در نظر می گیریم که از سهمی واقع در طرف چپ ناحیه تا خط واقع در طرف راست آن کشیده شده است.
این نوار از نقطه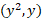 تا نقطه
تا نقطه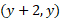 امتداد دارد. طول نوار
امتداد دارد. طول نوار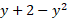 و عرض آن
و عرض آن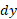 است. بنابراین مساحت نوار برابر است با
است. بنابراین مساحت نوار برابر است با 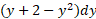 . مساحت ناحیه بین خم ها را با انتگرال گیری از
. مساحت ناحیه بین خم ها را با انتگرال گیری از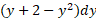 از
از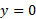 تا
تا 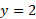 به دست می آوریم
به دست می آوریم
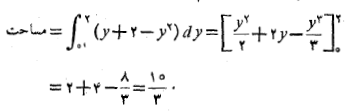
روش دوم. انتگرال گیری نسبت به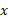 مطابق شکل زیر. در این مورد انتگرال گیری نسبت به
مطابق شکل زیر. در این مورد انتگرال گیری نسبت به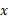 به آسانی انتگرال گیری نسبت به
به آسانی انتگرال گیری نسبت به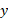 نیست. زیرا به جای یک انتگرال با دو انتگرال سرو کار خواهیم داشت. با حرکت دادن یک نوار قائم در سراسر ناحیه، از
نیست. زیرا به جای یک انتگرال با دو انتگرال سرو کار خواهیم داشت. با حرکت دادن یک نوار قائم در سراسر ناحیه، از 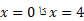 ، فرمول طول نوار در
، فرمول طول نوار در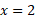 عوض می شود. طول نوار در سمت چپ
عوض می شود. طول نوار در سمت چپ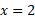 برابر با
برابر با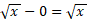 و درسمت راست
و درسمت راست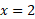 برابر با
برابر با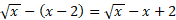 است. برای یافتن مساحت قسمت چپ نقطه
است. برای یافتن مساحت قسمت چپ نقطه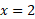 ، انتگرال
، انتگرال 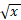 را از
را از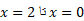 محاسبه می کنیم.
محاسبه می کنیم.
برای یافتن مساحت سمت راست، انتگرال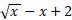 را از
را از 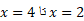 حساب می کنیم. سپس برای یافتن مساحت کل ناحیه ، نتایج را با هم جمع می کنیم
حساب می کنیم. سپس برای یافتن مساحت کل ناحیه ، نتایج را با هم جمع می کنیم
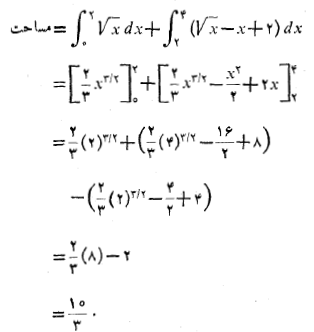
روش سوم. تفریق مساحت های شکل زیر. این روش به علت شکل هندسی این مساله خاص سریع ترین روش است. مساحتی که می خواهیم حساب کنیم، تفاضل مساحت مثلث با قاعده 2 و ارتفاع 2 است از مساحت ناحیه بین محور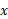 و خم
و خم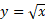 ، روی بازه
، روی بازه 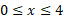 ؛
؛
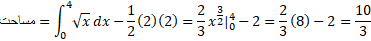
مثال 2 نشان می دهد که گاه یافتن مساحت یک ناحیه به کمک انتگرال گیری نسبت به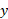 ساده تر است تا به کمک انتگرال گیری نسبت به
ساده تر است تا به کمک انتگرال گیری نسبت به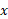 . بنابراین بهتر است قبلا ناحیه را بررسی کنیم تا روشن شود کدام روش، در صورتی که هردو روش را بتوان به کار برد، آسانتر است. همان طور که در روش3 مثال بالا دیدیم شکل ناحیه نیز ممکن است نشان دهد که چگونه از هندسه برای ساده کردن محاسبات استفاده کنیم.
. بنابراین بهتر است قبلا ناحیه را بررسی کنیم تا روشن شود کدام روش، در صورتی که هردو روش را بتوان به کار برد، آسانتر است. همان طور که در روش3 مثال بالا دیدیم شکل ناحیه نیز ممکن است نشان دهد که چگونه از هندسه برای ساده کردن محاسبات استفاده کنیم.
محاسبه حجم به روش برش دادن. حجم اجسام دورانی
اکنون که می توانیم مساحت بسیاری از نواحی مسطح را حساب کنیم، می توانیم روش تشکیل مجموعهای ریمان را تعمیم دهیم و حجم اجسامی را که این نواحی سطح مقطع های آن ها هستند به دست آوریم.
روش برش دادن
در وهله اول حجم استوانه ای را که مساحت قاعده آن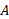 و ارتفاعش
و ارتفاعش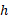 است به صورت
است به صورت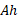 تعریف می کنیم. این تعریف تعمیمی است از فرمول زیر(در هندسه قضایی) در مورد استوانه های مستدیر به استوانه هایی با قاعده های دلخواه، نظیر استوانه ای که در شکل زیردیده می شود.
تعریف می کنیم. این تعریف تعمیمی است از فرمول زیر(در هندسه قضایی) در مورد استوانه های مستدیر به استوانه هایی با قاعده های دلخواه، نظیر استوانه ای که در شکل زیردیده می شود.
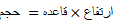
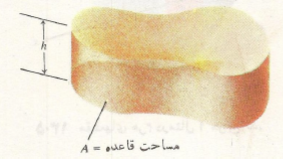
اکنون فرض کنید می خواهیم حجم جسمی را محاسبه کنیم که در شکل زیر دیده می شود.جسم به صفحاتی محدود است که در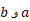 بر محور
بر محور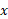 عمودند و شکلش بین این دو صفحه تغییر می کند. بدیهی است که این جسم حجمی دارد، اما چگونه این حجم را محاسبه کنیم و یا حتی آن را تعریف کنیم؟
عمودند و شکلش بین این دو صفحه تغییر می کند. بدیهی است که این جسم حجمی دارد، اما چگونه این حجم را محاسبه کنیم و یا حتی آن را تعریف کنیم؟
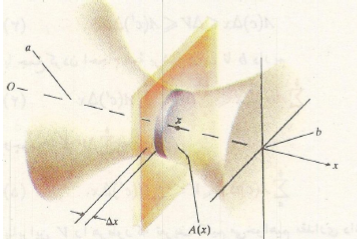
فرض می کنیم جسم را صفحاتی عمود بر محور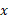 قطع کنند و به صورت برش های نازکی به ضخامت
قطع کنند و به صورت برش های نازکی به ضخامت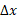 درآورند. به این ترتیب
درآورند. به این ترتیب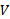 ، حجم جسم، برابر با مجموع حجم های این برش ها است. اما چگونه می توان
، حجم جسم، برابر با مجموع حجم های این برش ها است. اما چگونه می توان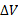 را تعریف کنیم، میل داریم که این جسم حداقل برابر
را تعریف کنیم، میل داریم که این جسم حداقل برابر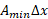 باشد، یعنی برابر با حجم استوانه ای که قاعده آن سطح مقطعی از برش با کمترین مساحت است. در شکل زیر این استوانه همان استوانه کوچک داخل برش است.
باشد، یعنی برابر با حجم استوانه ای که قاعده آن سطح مقطعی از برش با کمترین مساحت است. در شکل زیر این استوانه همان استوانه کوچک داخل برش است.
همچنین میل داریم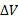 از
از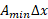 بزرگتر نباشد که این مقدار برابر حجم استوانه ای است که قاعده آن سطح مقطعی از برش با بیشترین مساحت است. این استوانه در شکل زیر استوانه بزرگی است که برش را در بردارد.
بزرگتر نباشد که این مقدار برابر حجم استوانه ای است که قاعده آن سطح مقطعی از برش با بیشترین مساحت است. این استوانه در شکل زیر استوانه بزرگی است که برش را در بردارد.
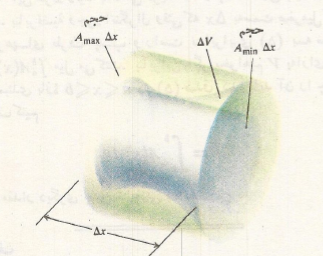
آنچه می خواهیم؛ با استفاده از نماد چنین است.
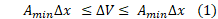
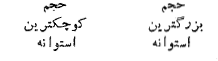
اگر مساحت سطح مقطع جسم در حالت عمود بر محور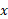 تابعی پیوسته چون
تابعی پیوسته چون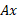 باشد، مقدار آن در بازه
باشد، مقدار آن در بازه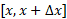 در نقطه ای چون
در نقطه ای چون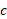 مینیمم و در نقطه ای چون
مینیمم و در نقطه ای چون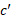 ماکسیمم است.
ماکسیمم است.
یعنی
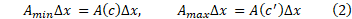
با اینجانشانی ها رابطه (1) چنین می شود

با جمع کردن احجام همه برش ها ازbتاa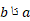 داریم
داریم
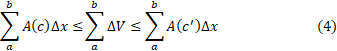
و چون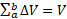 ، داریم
، داریم
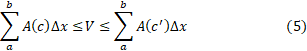
بنابراین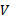 را هر طور که تعریف کنیم می خواهیم مقداری داشته باشد که به ازای هر تقسیم بندی بازه
را هر طور که تعریف کنیم می خواهیم مقداری داشته باشد که به ازای هر تقسیم بندی بازه 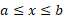 در نابرابری(5) صدق کند.
در نابرابری(5) صدق کند.
این شرط دقیقا به ما می گوید که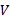 چه مقداری باید داشته باشد. بنا بر قضیه وجود انتگرال وقتی که
چه مقداری باید داشته باشد. بنا بر قضیه وجود انتگرال وقتی که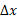 به سمت صفر میل کند مجموعه های طرف چپ و راست نابرابری(5) به سوی
به سمت صفر میل کند مجموعه های طرف چپ و راست نابرابری(5) به سوی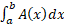 میل می کنند. بنابراین اگر بخواهیم
میل می کنند. بنابراین اگر بخواهیم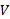 به ازای هر تقسیم بندی بازه
به ازای هر تقسیم بندی بازه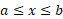 در (5) صدق کند، باید آن را چنین تعریف کنیم
در (5) صدق کند، باید آن را چنین تعریف کنیم
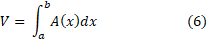
هیچ مقدار دیگری چنین خاصیتی را ندارد.
تعریف
حجم جسمی که مساحت سطح مقطع آن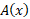 است از
است از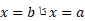 چنین به دست می آید
چنین به دست می آید
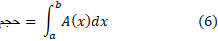
برای استفاده از این تعریف مادام که انتگرال وجود دارد لازم نیست که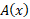 پیوسته باشد. مراحل عملی لازم برای محاسبه حجم اجسام به کمک تساوی (6) این ها هستند.
پیوسته باشد. مراحل عملی لازم برای محاسبه حجم اجسام به کمک تساوی (6) این ها هستند.
مرحله1: شکل جسم و یک سطح مقطع نمونه آن را می کشیم.
مرحله2: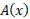 را می یابیم.
را می یابیم.
مرحله3: حدود انتگرال گیری را تعیین می کنیم.
مرحله4: انتگرال می گیریم.

 مثال1 قاعده هرمی به ارتفاع 3 متر، مربعی است به ضلع 3 متر. سطح مقطعی از هرم که عمود بر ارتفاع است و
مثال1 قاعده هرمی به ارتفاع 3 متر، مربعی است به ضلع 3 متر. سطح مقطعی از هرم که عمود بر ارتفاع است و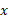 واحد از راس هرم فاصله دارد مربعی است به ضلع
واحد از راس هرم فاصله دارد مربعی است به ضلع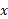 واحد. حجم هرم را بیابید.
واحد. حجم هرم را بیابید.
حل:هرم را چنان رسم می کنیم که ارتفاعش بر محور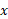 و رأسش بر مبدأ منطبق باشد. سپس یک سطح مقطع نمونه را می کشیم مطابق شکل.
و رأسش بر مبدأ منطبق باشد. سپس یک سطح مقطع نمونه را می کشیم مطابق شکل.
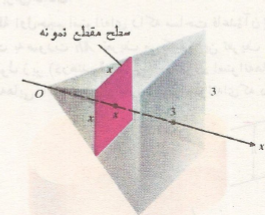
چون سطح مقطع مربعی به ضلع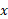 متر است، مساحتش برابر است با
متر است، مساحتش برابر است با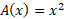 . حجم هرم برابر است با انتگرال
. حجم هرم برابر است با انتگرال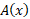 از
از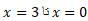 .
.
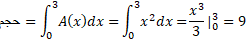
حجم برابر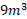 است که با مقدار زیر که از فرمول حجم هرم در هندسه فضایی به دست می آید یکی است.
است که با مقدار زیر که از فرمول حجم هرم در هندسه فضایی به دست می آید یکی است.
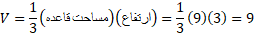
 مثال 2 از استوانه مستدیر قائمی به شعاع
مثال 2 از استوانه مستدیر قائمی به شعاع به وسیله دو صفحه، گوه خمیده ای می بریم. یکی از صفحات بر محور استوانه عمود است و دیگری با اولی زاویه حاده
به وسیله دو صفحه، گوه خمیده ای می بریم. یکی از صفحات بر محور استوانه عمود است و دیگری با اولی زاویه حاده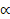 می سازد و آن را در مرکز استوانه قطع می کند. حجم گوه را بیابید.
می سازد و آن را در مرکز استوانه قطع می کند. حجم گوه را بیابید.
راه حل1: مقطع های عمود بر محور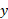 . گوه و یک مقطع نمونه عمود بر محور
. گوه و یک مقطع نمونه عمود بر محور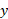 را رسم می کنیم مطابق شکل.
را رسم می کنیم مطابق شکل.
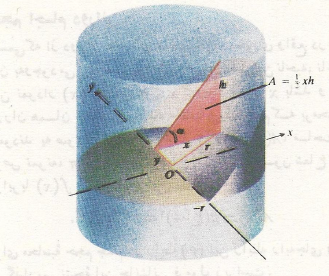
سطح مقطع مثلثی است با مساحت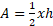
برای اینکه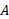 را برحسب
را برحسب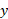 بیان کنیم، از رابطه مثلثاتی
بیان کنیم، از رابطه مثلثاتی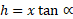 و رابطه زیر (قضیه فیثاعورس) استفاده می کنیم
و رابطه زیر (قضیه فیثاعورس) استفاده می کنیم
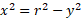 .
.
بنابراین داریم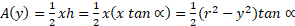
حجم گوه برابر است با انتگرال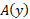 ازrتا-r
ازrتا-r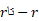 .
.
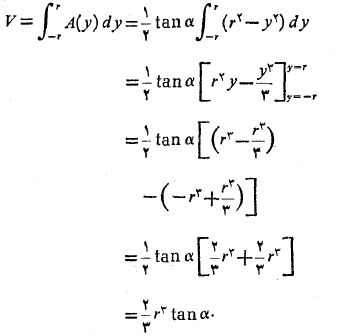
راه حل2: مقطع های عمود بر محور . در راه حل 1، استفاده از مقطع های عمود بر محور
. در راه حل 1، استفاده از مقطع های عمود بر محور اختیاری بود. اگر از مقطع های عمود بر محور
اختیاری بود. اگر از مقطع های عمود بر محور استفاده کنیم نتایجی به دست می آوریم که به همان اندازه راه حل1 مناسب اند همانند شکل.
استفاده کنیم نتایجی به دست می آوریم که به همان اندازه راه حل1 مناسب اند همانند شکل.
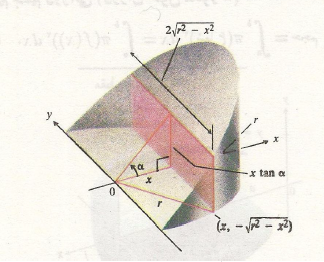
این مقاطع مستطیل اند و مساحت آن ها چنین به دست می آید
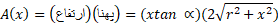
حجم گوه برابر است باانتگرال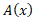 از
از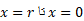 :
:
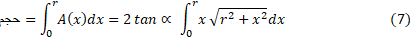
برای محاسبه انتگرال، ازجانشانی های زیر استفاده می کنیم
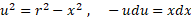
بنابراین
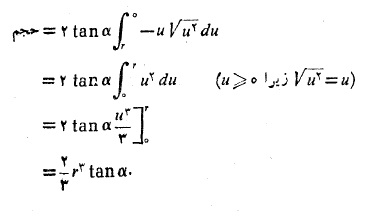
حجم جسم دورانی
جسمی که از دوران ناحیه ای مسطح حول محوری واقع در صفحه آن به وجود می آید جسم دورانی نام دارد. اگر این ناحیه، ناحیه ای بین نمودار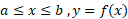 ، و محورx باشد و محور دوران همان محور
، و محورx باشد و محور دوران همان محور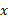 باشد، مقطع هایی از جسم که بر محور
باشد، مقطع هایی از جسم که بر محور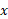 عمودند و به صورت قرص اند همانند شکل زیر.
عمودند و به صورت قرص اند همانند شکل زیر.
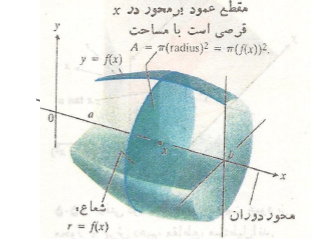
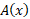 ، مساحت یک قرص نمونه،
، مساحت یک قرص نمونه،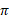 برابر مجذور شعاع آن است. چون شعاع در
برابر مجذور شعاع آن است. چون شعاع در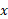 برابر با
برابر با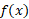 است داریم
است داریم
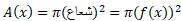
برای محاسبه حجم جسم در رابطه (6) این رابطه را به جای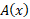 می گذاریم. نتیجه این جانشانی فرمول زیر است.
می گذاریم. نتیجه این جانشانی فرمول زیر است.
حجم جسم دورانی(دوران حول محور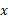 )
)
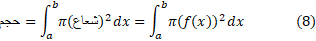
 مثال3 خم
مثال3 خم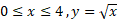 حول محور
حول محور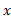 دوران می کند و جسم شکل زیر را بوجود می آورد. حجم این جسم را بیابید.
دوران می کند و جسم شکل زیر را بوجود می آورد. حجم این جسم را بیابید.

حل: شعاع قرص مقطع در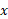 برابر است با
برابر است با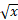 . بنابراین حجم جسم چنین به دست می آید
. بنابراین حجم جسم چنین به دست می آید
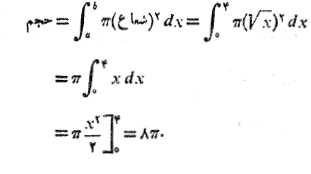
 مثال4 نیمدایره
مثال4 نیمدایره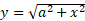 حول محور
حول محور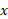 دوران می کند و یک کره به دست می آید. حجم این کره را بیابید.
دوران می کند و یک کره به دست می آید. حجم این کره را بیابید.
حل: کره و یک قرص مقطع نمونه را رسم می کنیم مطابق شکل.
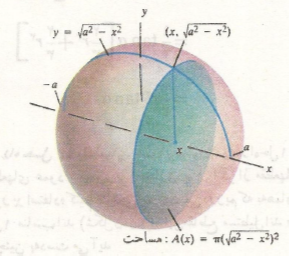
شعاع قرص برابر است با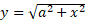 . بنابراین حجم کره چنین به دست می آید
. بنابراین حجم کره چنین به دست می آید
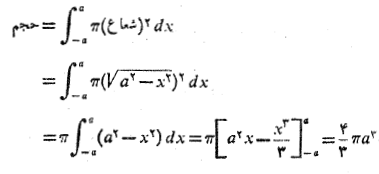
این نتیجه نیز مانند مثال1 با فرمول حجم مربوطه در هندسه فضایی مطابقت دارد.
برای یاد گیری مباحث بیشتر از محصولکپسول آموزشی ریاضی عمومی1 استفاده کنید.