قضیه اساسی حساب انتگرال
در این مقاله راهی را دنبال می کنیم که لایب نیتس و نیوتن پیش گرفتند تا نشان دهند چگونه می توان انتگرال های معین را به کمک حساب دیفرانسیل و انتگرال محاسبه کرد.
چنانچه خواهیم دیدهمه چیز از یک نکته اساسی به دست می آید: هرگاهf پیوسته باشد،انتگرال
پیوسته باشد،انتگرال
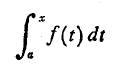
تابعی مشتق پذیر ازx است. این قضیه ارتباط بسیار مهم بین انتگرال های معین و پاد مشتق ها را به وجود می آورد.
است. این قضیه ارتباط بسیار مهم بین انتگرال های معین و پاد مشتق ها را به وجود می آورد.

توابعی که به کمک انتگرال تعریف می شوند: قضیه های اساسی حساب دیفرانسیل و انتگرال
انتگرال معین هرتابع پیوسته ای چون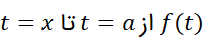 عددی مانند
عددی مانند
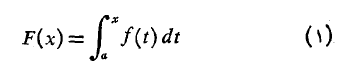
را تعریف می کند که می توان آن را به عنوان تابعی ازx در نظر گرفت. این انتگرال به ازای هر مقدارx
در نظر گرفت. این انتگرال به ازای هر مقدارx در دامنهf
در دامنهf ، خروجیF(x) به دست می دهد.
، خروجیF(x) به دست می دهد.
به این ترتیب راه مهمی برای تعریف توابع جدید به دست می آید. مثلا لگاریتم طبیعی عددی مثبت چونx را با فرمول زیر تعریف می کنیم.
را با فرمول زیر تعریف می کنیم.
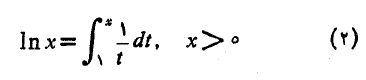
تابع خطای
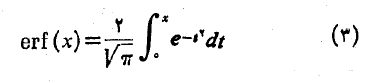
که در نظریه های احتمال، جریان گرما، و انتقال سیگنال به کار می رود وانتگرال سینوسی
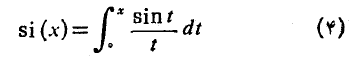
و نظایر آن که در مهندسی کاربرد دارند، نمونه هایی از تعریف تابع به کمک انتگرال اند.
برای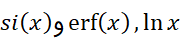 نه فرمولی ساده تر از معادلات(2) –(4) وجود دارد و نه به توصیف ساده تر آن ها نیازی هست. فرمول های انتگرالی، علی رغم نامانوس بودنشان، ما را قادر می سازند مقادیر توابعی را که تعریف می کنند،با هریک از روش های متعدد عددی برای تخمین زدن انتگرال ها، با دقت مطلوب محاسبه کنیم.
نه فرمولی ساده تر از معادلات(2) –(4) وجود دارد و نه به توصیف ساده تر آن ها نیازی هست. فرمول های انتگرالی، علی رغم نامانوس بودنشان، ما را قادر می سازند مقادیر توابعی را که تعریف می کنند،با هریک از روش های متعدد عددی برای تخمین زدن انتگرال ها، با دقت مطلوب محاسبه کنیم.
نوشتن مقدار لگاریتم طبیعی 2 به صورت
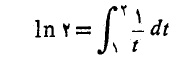
حقیقتا با نوشتن نسبت محیط یک دایره به قطرش به صورت π ، فرقی نمی کند. هیچ راهی برای نوشتن مقدار دقیق این نسبت وجود ندارد مگر نوشتن ان به صورت π
، فرقی نمی کند. هیچ راهی برای نوشتن مقدار دقیق این نسبت وجود ندارد مگر نوشتن ان به صورت π . اما هرگاه بخواهیم می توانیم تقریب عددی این نسبت را تا هر چند رقم اعشار که مطلوب باشد محاسبه کنیم.
. اما هرگاه بخواهیم می توانیم تقریب عددی این نسبت را تا هر چند رقم اعشار که مطلوب باشد محاسبه کنیم.
فرمول
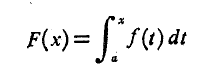
ارتباط میان پادمشتق و انتگرال معین را به دست می دهد: اگرf تابعی پیوسته باشد، آنگاهF
تابعی پیوسته باشد، آنگاهF تابعی مشتق پذیر ازx
تابعی مشتق پذیر ازx است، و
است، و
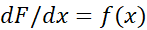 . اگر قرار باشد به جزیره ای لم یزرع تبعید شوید و تنها بتوانید با خود یک فرمول به همراه داشته باشید، فرمول
. اگر قرار باشد به جزیره ای لم یزرع تبعید شوید و تنها بتوانید با خود یک فرمول به همراه داشته باشید، فرمول
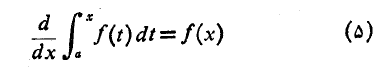
می تواند انتخاب خوبی باشد. این معادله حاکی است که معادله دیفرانسیل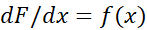 به ازای هر تابع پیوستهf
به ازای هر تابع پیوستهf جواب دارد. این معادله می گوید که هر تابع پیوسته ای
جواب دارد. این معادله می گوید که هر تابع پیوسته ای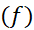 مشتق تابع دیگری
مشتق تابع دیگری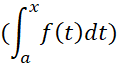 است. این معادله حاکی است که هر تابع پیوسته ای یک پادمشتق دارد. اهمیت معادله (5) آن قدر است که آن را نخستین قضیه اساسی حساب دیفرانسیل و انتگرال می نامیم.
است. این معادله حاکی است که هر تابع پیوسته ای یک پادمشتق دارد. اهمیت معادله (5) آن قدر است که آن را نخستین قضیه اساسی حساب دیفرانسیل و انتگرال می نامیم.
قضیه2
نخستین قضیه اساسی حساب دیفرانسیل و انتگرال
اگرf روی بازه
روی بازه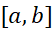 پیوسته باشد، آنگاه
پیوسته باشد، آنگاه
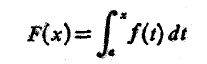
در هر نقطهx در
در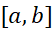 مشتق پذیر است و داریم
مشتق پذیر است و داریم
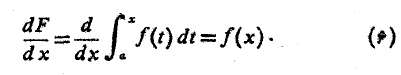

نتیجه
وجود پادمشتق تابع های پیوسته
اگر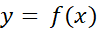 روی بازه
روی بازه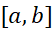 پیوسته باشد، آنگاه یک تابعF(x) وجود دارد که مشتقش روی
پیوسته باشد، آنگاه یک تابعF(x) وجود دارد که مشتقش روی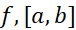 است.
است.
اثبات نتیجهفرض می کنیم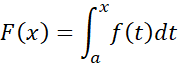 . بنا به قضیه وجود انتگرال و بنا به نخستین قضیه اساسی داریم
. بنا به قضیه وجود انتگرال و بنا به نخستین قضیه اساسی داریم 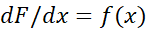 .
.
برای اثبات نخستین قضیه اساسی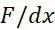 را به کمک تعریفش، به عنوان حد کسر زیر وقتی که
را به کمک تعریفش، به عنوان حد کسر زیر وقتی که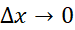 ، محاسبه می کنیم
، محاسبه می کنیم
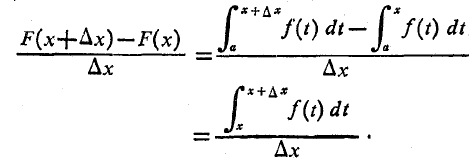
لذا حد زیر را حساب می کنیم
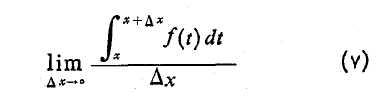
و نشان می دهیم که مقدار این حد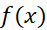 است. اما نخست نظری به تعبیر هندسی قضیه می افکنیم.
است. اما نخست نظری به تعبیر هندسی قضیه می افکنیم.
اگرf مثبت باشد، انتگرالش از
مثبت باشد، انتگرالش از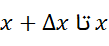 برابر با مساحت نوار زیر نمودار
برابر با مساحت نوار زیر نمودار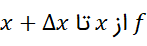 است.
است.
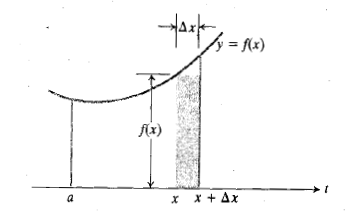
ارتفاع و پهنای نوار به ترتیب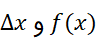 حدودا است.بنابراین
حدودا است.بنابراین
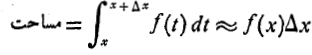
از تقسیم این رابطه به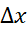 داریم
داریم
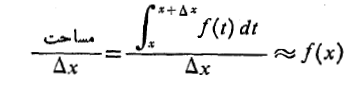
وقتی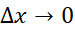 ، تقریب بهتر می شود، و انتظار داریم در حد، برابری به دست آید.
، تقریب بهتر می شود، و انتظار داریم در حد، برابری به دست آید.
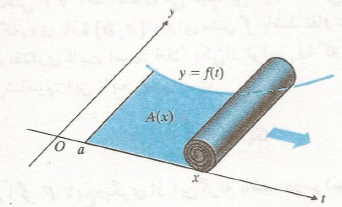
حال تعبیری از معادله(6) به کمک حرکت ارائه می دهیم. تصور کنید ناحیه زیر خم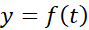 را با باز کردن فرشی به چهنای متغیر
را با باز کردن فرشی به چهنای متغیر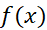 از چپ به راست می پوشانیم. آهنگ فرش شدن کف وقتی لوله فرش بهx
از چپ به راست می پوشانیم. آهنگ فرش شدن کف وقتی لوله فرش بهx می رسد
می رسد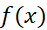 است.
است.
اثبات نخستین قضیه اساسی برای اثبات قضیه نشان می دهیم که برای هر تابع پیوستهf ،رابطه
،رابطه
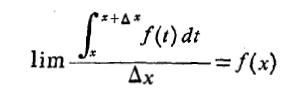
به ازای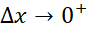 و به ازای
و به ازای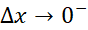 بر قرار است. این روش نشان می دهد که وقتی
بر قرار است. این روش نشان می دهد که وقتی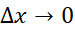 ، حد دو طرفه وجود دارد و برابر با
، حد دو طرفه وجود دارد و برابر با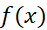 است.
است.
به ازای مقادیر مثبت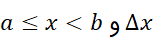 ، محاسبه به این صورت است: چون
، محاسبه به این صورت است: چون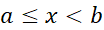 ، می توان با مقادیر آن چنان کوچکی از
، می توان با مقادیر آن چنان کوچکی از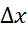 شروع کرد که
شروع کرد که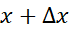 بین
بین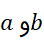 قرار گیرد.
قرار گیرد.
چونf در بازه بسته از
در بازه بسته از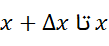 پیوسته است، در این بازه یک مقدار مینیمم
پیوسته است، در این بازه یک مقدار مینیمم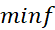 ، و یک مقدار ماکسیمم
، و یک مقدار ماکسیمم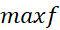 دارد.
دارد.
بنابراین با به کار بردن نابرابری انتگرالی در مورد بازه
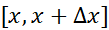 داریم
داریم
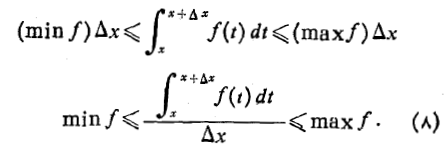
چونf پیوسته است، در نقطه ای چونc
پیوسته است، در نقطه ای چونc از بازه
از بازه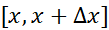 ماکسیمم و در نقطه ای چونc' از این بازه مینیمم می شود. یعنی
ماکسیمم و در نقطه ای چونc' از این بازه مینیمم می شود. یعنی
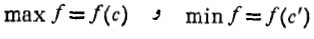
با اینجانشانی ها معادله(8) چنین می شود
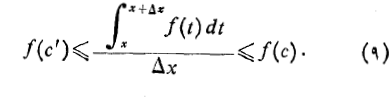
وقتی که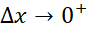 ، چونcوc' بین
، چونcوc' بین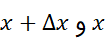 قرار دارند هر دو بهx
قرار دارند هر دو بهx میل می کنند و چونf
میل می کنند و چونf درx
درx پیوسته است،
پیوسته است،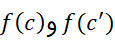 هر دو به
هر دو به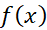 میل می کنند. بنابراین طرف راست و چپ معادله(9) هر دو به
میل می کنند. بنابراین طرف راست و چپ معادله(9) هر دو به
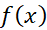 میل می کنند و با استفاده از قضیه ساندویچ داریم
میل می کنند و با استفاده از قضیه ساندویچ داریم
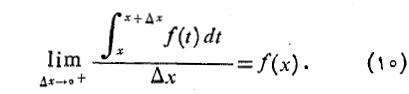
استدلال مشابهی نشان می دهد که وقتی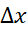 منفی باشد و
منفی باشد و
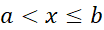 ، داریم
، داریم
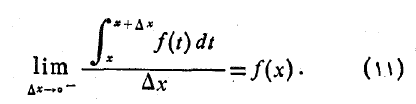
معادلات (10) و (11) همراه با هم چنین نتیجه می دهند که در هر نقطه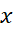 از
از 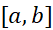 داریم
داریم
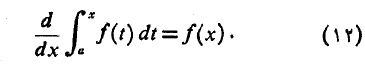
به این ترتیب نخستین قضیه اساسی اثبات می شود.
 مثال 1
مثال 1
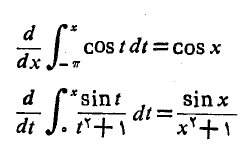
 مثال2 اگر
مثال2 اگر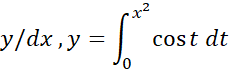 را بیابید.
را بیابید.
حل: کلید حل این مسالهقاعده زنجیریاست.y را به صورت ترکیب زیر در نظر می گیریم.
را به صورت ترکیب زیر در نظر می گیریم.
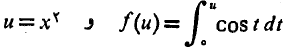
با استفاده از قاعده زنجیری به صورت
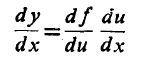
داریم
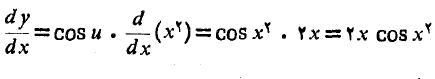
بنابراین
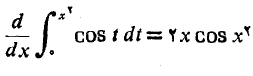
 مثال 3 اگر
مثال 3 اگر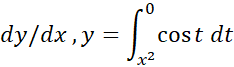 را بیابید.
را بیابید.
حل: در این مساله حد متغیر انتگرال گیری حد پایینی است و نه حد بالایی، بنابراین قبل از به کار بردن نخستین قضیه اساسی باید حدودانتگرال گیری را عوض کنیم.
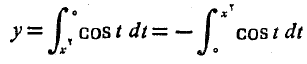
حال می توان نتیجه مثال 2 را به کار برد:
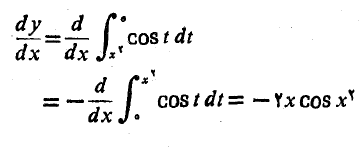
قضیه تعیین مقدار انتگرال
اکنون به قضیه مهمی می پردازیم که چگونگی استفاده از پاد مشتق در تعیین مقدار انتگرال معین را مشخص می کند. با در اختیار داشتن این قضیه دیگر مجبور نخواهیم بود انتگرال معین را به صورت حد حساب کنیم. سودمندی این قضیه به اندازه ای است که اغلب آن را دومین قضیه اساسی حساب دیفرانسیل و انتگرال می نامند.
قضیه 2
قضیه تعیین مقدار انتگرال (دومین قضیه اساسی حساب دیفرانسیل و انتگرال)
اگرf در هر نقطه ای از
در هر نقطه ای از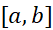 پیوسته باشد، وF
پیوسته باشد، وF هر پاد مشتقی ازf
هر پاد مشتقی ازf روی
روی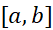 باشد، آنگاه
باشد، آنگاه
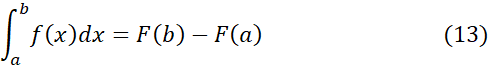
قضیه تعیین مقدار انتگرال حاکی است که برای محاسبه انتگرالf روی
روی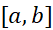 کافی است چنین کنیم:
کافی است چنین کنیم:
1.پادمشتقی چونF ازf
ازf را به دست آوریم، و
را به دست آوریم، و
2.مقدار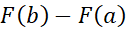 را حساب کنیم.
را حساب کنیم.
این مقدار برابر با 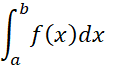 خواهد بود. بنا به نخستین قضیه اساسی، وجود پاد مشتقF
خواهد بود. بنا به نخستین قضیه اساسی، وجود پاد مشتقF حتمی است. برای انجام محاسبه، کافی استF
حتمی است. برای انجام محاسبه، کافی استF را بیابیم و مقدار آن را تعیین کنیم.
را بیابیم و مقدار آن را تعیین کنیم.
اثباتبرای اثبات این قضیه از نتیجه 3ی قضیه مقدار میانگین استفاده می کنیم. این نتیجه حاکی است هر دو تابعی که روی بازه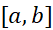 دارای مشتقf
دارای مشتقf باشند تفاوتشان روی این بازه مقداری ثابت است. فعلا یکی از توابعی را که مشتقشf
باشند تفاوتشان روی این بازه مقداری ثابت است. فعلا یکی از توابعی را که مشتقشf است را می شناسیم. این تابع چنین است
است را می شناسیم. این تابع چنین است
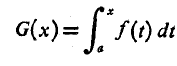
بنابراین اگرF تابع دیگری از این گونه باشد، در سراسر
تابع دیگری از این گونه باشد، در سراسر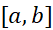 به ازای مقدار ثابتی مانندCداریم
به ازای مقدار ثابتی مانندCداریم
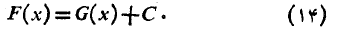
اگر برای محاسبه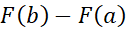 معادله(14) را به کار ببریم
معادله(14) را به کار ببریم
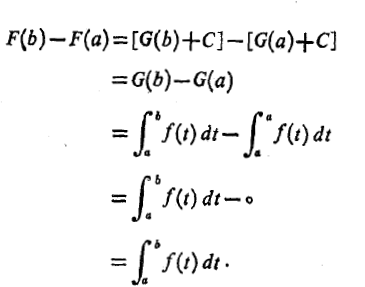
که همان معادله (13) است.
مرسوم است که برای مقدار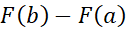 نماد
نماد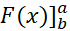 را به کار ببرند؛ ما نیز در مثال های زیر از این نماد استفاد می کنیم.
را به کار ببرند؛ ما نیز در مثال های زیر از این نماد استفاد می کنیم.
 مثال4 مساحت ناحیه زیر خط
مثال4 مساحت ناحیه زیر خط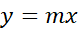 را بیابید.
را بیابید.
حل:
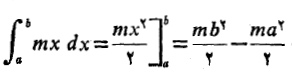
 مثال5 مساحت ناحیه زیر خم
مثال5 مساحت ناحیه زیر خم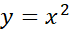 را بیابید.
را بیابید.
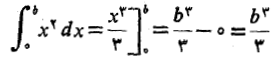

 مثال6 مساحت ناحیه محصور بین محورx
مثال6 مساحت ناحیه محصور بین محورx و یکی از قوس های خم
و یکی از قوس های خم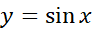 را بیابید.
را بیابید.
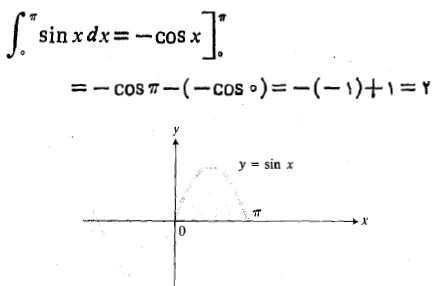
حل: قوس بین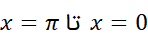 را بر می گزینیم.مساحت محصور بین این قوس و محورx
را بر می گزینیم.مساحت محصور بین این قوس و محورx چنین است
چنین است
 مثال7 در این مثال از چند ویژگی جبری انتگرال های معین استفاده می کنیم.
مثال7 در این مثال از چند ویژگی جبری انتگرال های معین استفاده می کنیم.
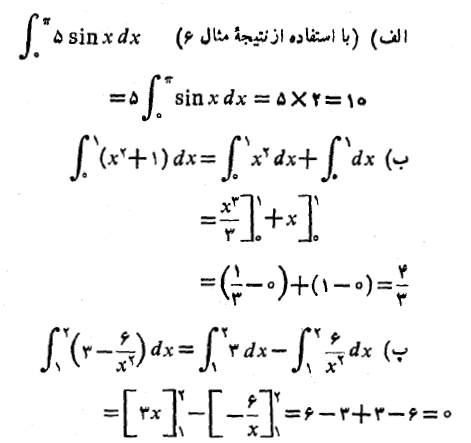
اگر تابع پیوسته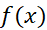 روی بازه
روی بازه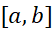 مقدار منفی نداشته باشد، انتگرالش از bتاa برابر مساحت بین نمودارش و محورx
مقدار منفی نداشته باشد، انتگرالش از bتاa برابر مساحت بین نمودارش و محورx است.
است.
اگرf روی این بازه منفی یا نامثبت باشد، چنانکه در مثال بعد می بینیم،انتگرالش برابر با قرینه این مساحت است.
روی این بازه منفی یا نامثبت باشد، چنانکه در مثال بعد می بینیم،انتگرالش برابر با قرینه این مساحت است.
 مثال 8 با توجه به شکل مطلوب است تعیین
مثال 8 با توجه به شکل مطلوب است تعیین
الف) مساحت ناحیه بین خم 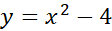 و محورx
و محورx از
از
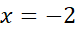 تا
تا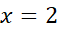
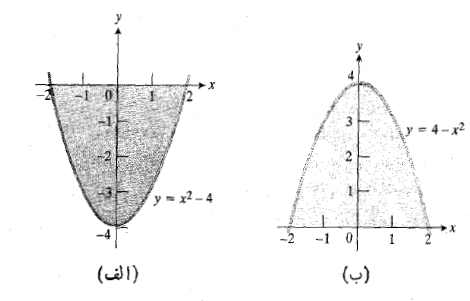
ب)مساحت ناحیه بین خم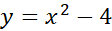 و محورx
و محورx از
از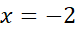 تا
تا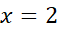
حل:
الف) انتگرال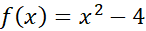 روی بازه از 2- تا 2 چنین است
روی بازه از 2- تا 2 چنین است
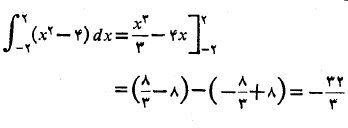
مساحت بین خم و محورx از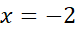 تا
تا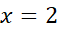 برابر با32/3 واحد مساحت است.
برابر با32/3 واحد مساحت است.
ب) نمودار
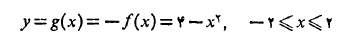
که در قسمت (ب) شکل دیده می شود تصویر آینه ای نمودارf نسبت به محورx
نسبت به محورx است. مساحت بین نمودار gو محورx
است. مساحت بین نمودار gو محورx
چنین است
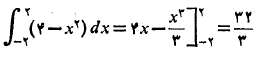
اگر مطابق شکل زیر بخشی از نمودار تابعی چونf روی بازه
روی بازه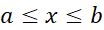 در بالای محورx
در بالای محورx و بخشی در زیر محورx
و بخشی در زیر محورx باشد، انتگرالf روی این بازه جمع جبری مساحت های علامت دار است.
باشد، انتگرالf روی این بازه جمع جبری مساحت های علامت دار است.
مساحت های بالای محور را مثبت و مساحت های زیر محور را منفی در نظر می گیریم. در چنین حالتی مقدار انتگرال از کل مساحت ناحیه بین خم و محورx کمتر است.
کمتر است.
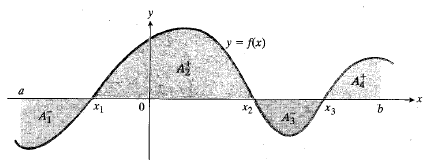
مثلا اگر در شکل فوق قدر مطلق های مساحت های بین خم و محور
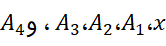 باشند، آنگاه
باشند، آنگاه
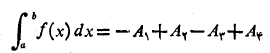
که کمتر از مساحت کل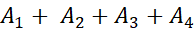 است. برای محاسبه مساحت کل، نقاط
است. برای محاسبه مساحت کل، نقاط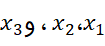 یعنی محل تقاطع خم با محورx
یعنی محل تقاطع خم با محورx را تعیین می کنیم و انتگرال هر قسمت را جداگانه به دست می آوریم
را تعیین می کنیم و انتگرال هر قسمت را جداگانه به دست می آوریم
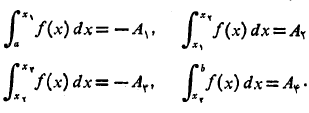
سپس قدر مطلق های این انتگرال ها را با هم جمع می کنیم.
 مثال9 مساحت ناحیه بین خم
مثال9 مساحت ناحیه بین خم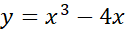 و محورx
و محورx را بیابید.
را بیابید.
حل: برای تعیین شکل و حدودانتگرال گیری نمودار
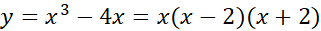 را رسم می کنیم(شکل زیر).
را رسم می کنیم(شکل زیر).
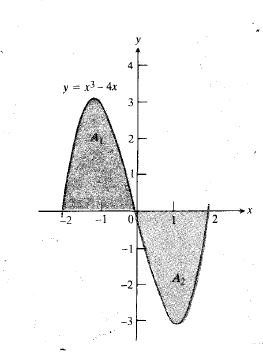
خم از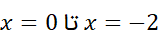 بالای محورx
بالای محورx و از
و از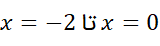 زیر محورx
زیر محورx قرار دارد. انتگرال های زیر را حساب می کنیم:
قرار دارد. انتگرال های زیر را حساب می کنیم:
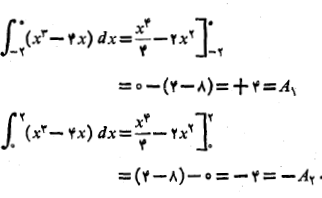
مساحت ناحیه برابر است با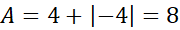 .
.
فرمول های جانشانی برای انتگرال های معین
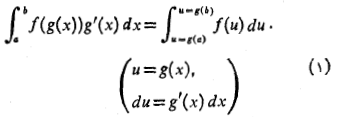
اگرg' روی بازه از 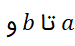
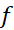 روی مجموعه مقادیری کهg اختیار می کند پیوسته باشند، فرمول بالا برقرار است.
روی مجموعه مقادیری کهg اختیار می کند پیوسته باشند، فرمول بالا برقرار است.
برای اثبات رابطه(1)، فرض می کنیمF پاد مشتقی ازf
پاد مشتقی ازf باشد. بنابراین
باشد. بنابراین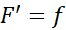 . پس
. پس
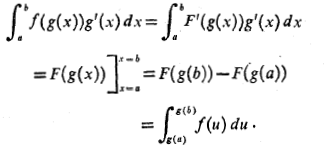
 مثال1 به کمک رابطه(1) انتگرال زیر را حساب کنید
مثال1 به کمک رابطه(1) انتگرال زیر را حساب کنید
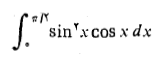
حل: از جانشانی های زیر استفاده می کنیم
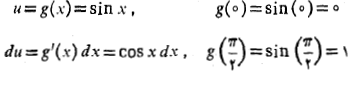
بنابراین داریم
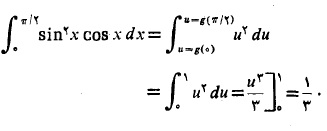
 مثال2 انتگرال زیر را حساب کنید
مثال2 انتگرال زیر را حساب کنید
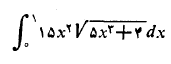
حل: از دو راه می توان مساله را حل کرد
راه اول: انتگرال را تبدیل می کنیم و مانند رابطه(1) انتگرال تبدیل شده را با حدود تبدیل شده محاسبه می کنیم.
جانشانی های زیر را انجام می دهیم
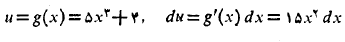
بنابراین
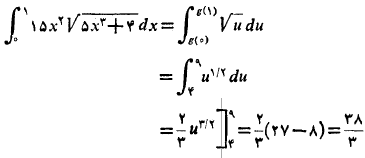
راه دوم: مانند قبل انتگرال را تبدیل می کنیم، و انتگرال حاصل را محاسبه می کنیم. سپس معکوس آن را بر حسبx می نویسیم و از حدود اصلی بر حسبx
می نویسیم و از حدود اصلی بر حسبx استفاده می کنیم.
استفاده می کنیم.
با جانشانی های زیر
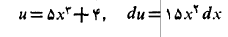
داریم
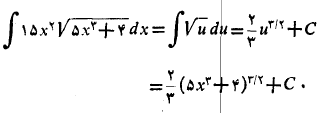
بنابراین
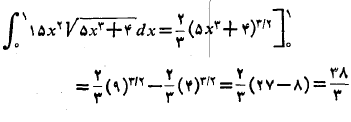
کدام یک از این روش ها بهتر است: محاسبهانتگرال تبدیل شده با حدود تبدیل شده یا محاسبه انتگرال اصلی با حدود اصلی؟ در این مثال هر دو روش مناسب اند، اما گاه یک روش از روش دیگر آسانتر است. به طور کلی، بهتر است با هر دو روش آشنا باشیم، و بر حسب مورد روش بهتر را برگزینیم.
جهت مطالعه مباحث بیشتر از محصولکپسول ریاضی عمومی 1 استفاده کنید.