قواعدی برای تقریب زدن انتگرال های معین
برای محاسبه انتگرال های معین توابعی نظیر
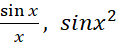
و
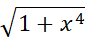
که پاد مشتق هایشان فرمول ساده ای ندارند، از روش های عددی نظیر قاعده ذوزنقه ای و قاعده سیمپسون استفاده می کنیم. به کمک این قواعد همچنین می توانیم انتگرال یک تابع را از جدول مقادیرش، حتی اگرفرمولی برای آن تابع دراختیار نداشته باشیم، به دست آوریم.
چنین حالتی وقتی پیش می آید که اطلاعات ما درباره یک تابع به صورت مجموعه ای از مقادیرخاص باشد که در آزمایشگاه یا ضمن کار به دست می آید.

قاعده ذوزنقه ای
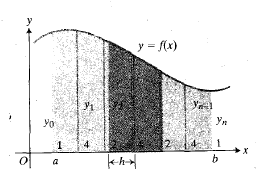
قاعده ذوزنقه ای برای محاسبه مقدار یکانتگرال معین بر پایه تقریب زدن ناحیه بین یک خم و محور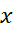 به کمک ذوزنقه ها به جای مستطیل ها استوار است (شکل زیر).
به کمک ذوزنقه ها به جای مستطیل ها استوار است (شکل زیر).
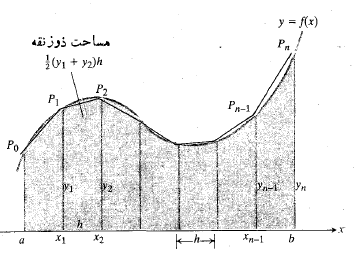
طول زیر بازه هایی که از تقسیم بازه به کمک نقاط 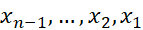 به دست می آیند ضرورتی ندارد برابر باشند، اما اگر برابر باشند فرمول حاصل ساده تر می شود. بنابراین فرض می کنیم طول هر بازه چنین باشد:
به دست می آیند ضرورتی ندارد برابر باشند، اما اگر برابر باشند فرمول حاصل ساده تر می شود. بنابراین فرض می کنیم طول هر بازه چنین باشد:
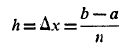
به این ترتیب مجموع مساحت های ذوزنقه ها برابراند با
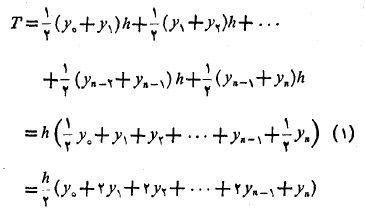
که در آن
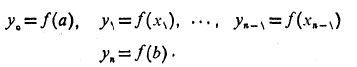
قاعده ذوزنقه ای می گوید که«برای برآورد کردن انتگرال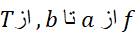 استفاده کنید».
استفاده کنید».
قاعده ذوزنقه ای
برایتقریب زدن
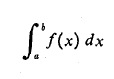
از رابطه
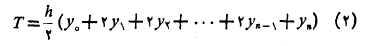
استفاده کنید. ( طول هریک از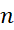 زیر بازه،
زیر بازه،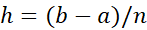 است.)
است.)
 مثال1 برای تقریب زدن انتگرال زیر از قاعده ذوزنقه ای با ضابطه
مثال1 برای تقریب زدن انتگرال زیر از قاعده ذوزنقه ای با ضابطه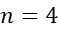 استفاده کنید.
استفاده کنید.
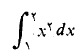
مقدار تقریبی به دست آمده را با مقدار دقیق انتگرال مقایسه کنید.
حل: مقدار دقیق انتگرال چنین است
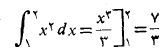
برای یافتن تقریب ذوزنقه ای، بازه انتگرال گیری را به چهار زیر بازه انتهایی و نقاط میانی فهرست می کنیم(جدول زیر).
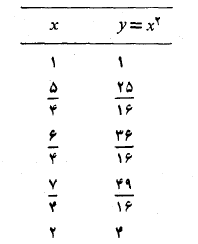
سپس رابطه (2) را به ازای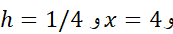 محاسبه می کنیم
محاسبه می کنیم
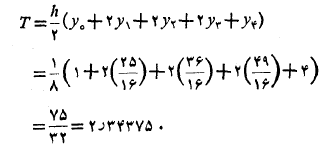
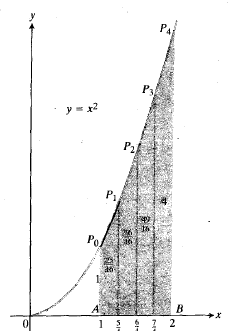
مقدار تقریبی مساحت، حدود نیم درصد از مقدار واقعی آن بیشتر است زیرا هر ذوزنقه قدری بزرگتر از نوار نظیر زیر خم است (شکل زیر)
برآورد خطا در قاعده ذوزنقه ای
با افزایش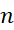 و میل کردن طول زیر بازه ها،
و میل کردن طول زیر بازه ها،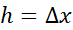 ، به سمت صفر،
، به سمت صفر،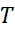 به سمت مقدار دقیق
به سمت مقدار دقیق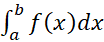 میل می کند. علت این امر این است
میل می کند. علت این امر این است
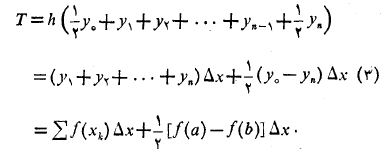
وقتی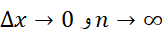 داریم
داریم
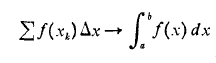
و
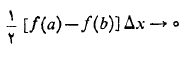
بنابراین
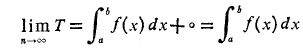
یعنی از لحاظ نظری می توانیم با انتخاب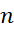 ی که به اندازه کافی بزرگ باشد تفاضل
ی که به اندازه کافی بزرگ باشد تفاضل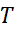 وانتگرال را تا آنجا که بخواهیم کوچک کنیم. اما واقعا
وانتگرال را تا آنجا که بخواهیم کوچک کنیم. اما واقعا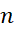 باید چقدر بزرگ باشد تا خطا از حد معینی تجاوز نکند؟
باید چقدر بزرگ باشد تا خطا از حد معینی تجاوز نکند؟
این سوال را به کمک نتیجه ای از حساب دیفرانسیل و انتگرال پیشرفته پاسخ می گوییم. بنا به نتیجه اگر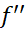 روی
روی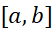 پیوسته باشد، به ازای عددی چون
پیوسته باشد، به ازای عددی چون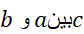 داریم
داریم
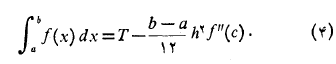
بنابراین وقتی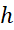 به سمت صفر میل کند، خطا،
به سمت صفر میل کند، خطا،
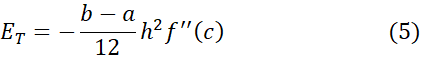
به صورت مجذور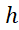 به سمت صفر میل می کند.
به سمت صفر میل می کند.
نا برابری
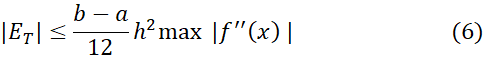
که در آن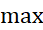 به بازه
به بازه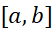 مربوط می شود، یک کران بالا برای اندازه خطا به دست می دهد. معمولا در عمل نمی توانیم مقدار دقیق
مربوط می شود، یک کران بالا برای اندازه خطا به دست می دهد. معمولا در عمل نمی توانیم مقدار دقیق 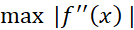 را به دست آوریم و باید یک کران بالا یا «بدترین حالت» را به جای آن برآورد کنیم.
را به دست آوریم و باید یک کران بالا یا «بدترین حالت» را به جای آن برآورد کنیم.
اگر 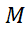 یک کران بالا برای مقادیر
یک کران بالا برای مقادیر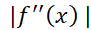 روی
روی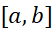 باشد، آنگاه
باشد، آنگاه
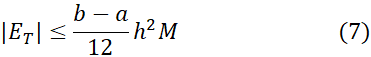
معمولا برای برآورد کردن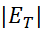 این نابرابری را به کار می بریم. بهترین
این نابرابری را به کار می بریم. بهترین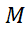 ی را که می توانیم بیابیم تعیین می کنیم و به کمک آن
ی را که می توانیم بیابیم تعیین می کنیم و به کمک آن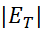 را برآورد می کنیم.
را برآورد می کنیم.
ممکن است این فرمول جواب های دقیق به دست ندهد. برای اینکه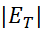 به ازای یک
به ازای یک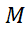 مفروض کوچک باشد،
مفروض کوچک باشد،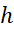 را کوچک می گیریم.
را کوچک می گیریم.
برآورد خطا در قاعده ذوزنقه ای
اگر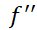 پیوسته و
پیوسته و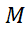 یک کران بالا برای مقادیر
یک کران بالا برای مقادیر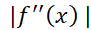 روی
روی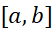 باشد، آنگاه خطای
باشد، آنگاه خطای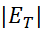 در تقریب ذوزنقه ای انتگرال
در تقریب ذوزنقه ای انتگرال 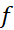 ااز
ااز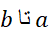 در نا برابری زیر صدق می کند
در نا برابری زیر صدق می کند
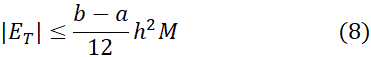
 مثال2 یک کران بالا برای خطای تقریبی که در مثال 1 برای انتگرال زیر به دست آوردیم، بیابید
مثال2 یک کران بالا برای خطای تقریبی که در مثال 1 برای انتگرال زیر به دست آوردیم، بیابید
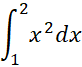
نخست یک کران بالا چون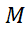 برای اندازهمشتق دوم
برای اندازهمشتق دوم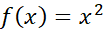 روی بازه
روی بازه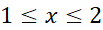 می یابیم. چون به ازای همه
می یابیم. چون به ازای همه 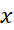
 ها داریم
ها داریم 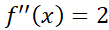 ، با اطمینان
، با اطمینان 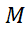 را برابر با 2 می گیریم. به ازای
را برابر با 2 می گیریم. به ازای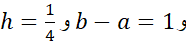 ، معادله (8) چنین می شود
، معادله (8) چنین می شود
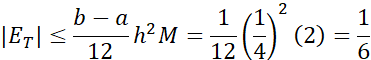
که دقیقا برابر با تفاضل 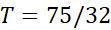 از
از 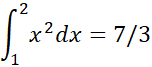 یعنی
یعنی
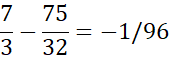 است.
است.
در این مثال توانستیم مقداردقیق خطا را به دست دهیم زیرامشتق دوم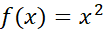 ثابت است و درانتخاب جمله
ثابت است و درانتخاب جمله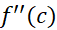 در معادله (4) تردید نداشتیم. اما هماره این چنین بخت یار نیست و در اکثر موارد بهترین کاری که می توانیم بکنیم این است که تفاضل
در معادله (4) تردید نداشتیم. اما هماره این چنین بخت یار نیست و در اکثر موارد بهترین کاری که می توانیم بکنیم این است که تفاضل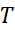 وانتگرال را تا آنجا که بخواهیم برآورد کنیم.
وانتگرال را تا آنجا که بخواهیم برآورد کنیم.
 مثال 3 قرار است برای برآورد مقدار انتگرال زیر با
مثال 3 قرار است برای برآورد مقدار انتگرال زیر با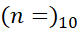 گام قاعده ذوزنقه ای را به کار ببریم
گام قاعده ذوزنقه ای را به کار ببریم
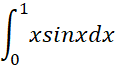
یک حد بالا برای خطای حاصل از این برآورد بیابید.
حل: فرمول زیر را به ازای 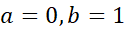 و
و 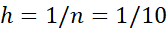 به کار می بریم
به کار می بریم
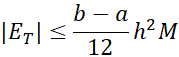
بنابراین
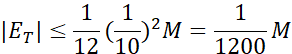
عدد 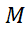 می تواند هر کران بالایی برای مقادیر
می تواند هر کران بالایی برای مقادیر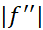 روی
روی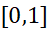 باشد. برای انتخاب مقداری برای
باشد. برای انتخاب مقداری برای 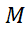 و
و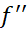 را محاسبه می کنیم تا از میزان بزرگی آن آگاه شویم. بامشتق گیری مستقیم داریم
را محاسبه می کنیم تا از میزان بزرگی آن آگاه شویم. بامشتق گیری مستقیم داریم
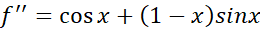
بنابراین چون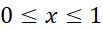 و
و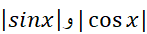 هرگز از 1 بزرگتر نخواهد شد، داریم
هرگز از 1 بزرگتر نخواهد شد، داریم
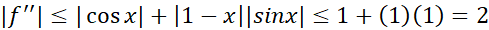
از این رو با اطمینان می توان 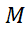 را برابر با 2 برگزید. پس
را برابر با 2 برگزید. پس
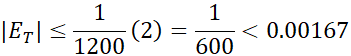
خطا از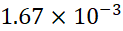 بیشتر نیست.
بیشتر نیست.
برای به دست آوردن دقت بیشتر 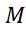 را تصحیح نمی کنیم بلکه گام های بیشتری بر می داریم. مثلا ل به ازای
را تصحیح نمی کنیم بلکه گام های بیشتری بر می داریم. مثلا ل به ازای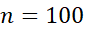 و
و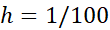 داریم
داریم
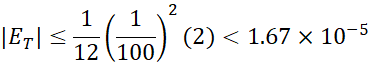
 مثال4 برای تقریب زدن
مثال4 برای تقریب زدن
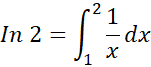
کمک قاعده ذوزنقه ای، چند تقسیم باید انجام شود تا قدر مطلق خطا کمتر از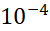 باشد؟
باشد؟
حل: برای تعیین تعداد تقسیمات،
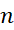 ، معادله (8) را به ازای
، معادله (8) را به ازای
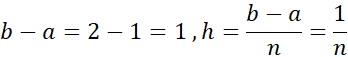
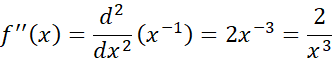
به کار می بریم و به دست می آوریم
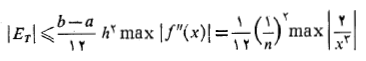
که در آن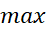 به بازه
به بازه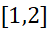 مربوط می شود. این حالت که در آن عملا می توانیم
مربوط می شود. این حالت که در آن عملا می توانیم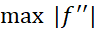 را بیابیم و مجبور نیستیم یک کران بالا به جای آن قرار دهیم به ندرت پیش می آید.
را بیابیم و مجبور نیستیم یک کران بالا به جای آن قرار دهیم به ندرت پیش می آید.
روی بازه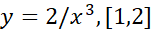 به تدریج ازماکسیمم،
به تدریج ازماکسیمم،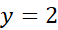 ، به مینیمم،
، به مینیمم، 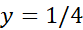 ، کاهش می یابد(شکل زیر).
، کاهش می یابد(شکل زیر).
بنابراین
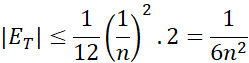
پس قدر مطلق خطا در صورتی کمتر از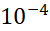 است که
است که
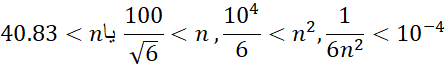
نخستین عدد صحیح بزرگتر از40.83 برابر است با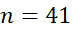 .
.
با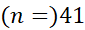 تقسیم می توان تضمین کرد که اندازه خطای محاسبه
تقسیم می توان تضمین کرد که اندازه خطای محاسبه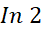 کمتراز
کمتراز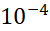 است. برای هر
است. برای هر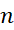
 بزرگتری نیز چنین است.
بزرگتری نیز چنین است.
قاعده سیمپسون
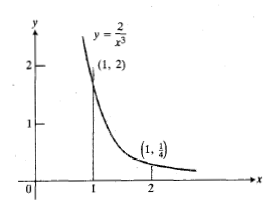
هر سه نقطه ای از یک صفحه را که روی یک خط راست واقع نباشند می توان روی یک سهمی جای داد. قاعده سیمپسون برپایه تقریب زدن خم ها با سهمی ها (به عوض ذوزنقه ها) استوار است. مساحت سایه دار زیر سهمی در شکل چنین است
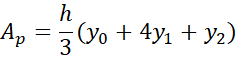
با کاربرد پیاپی این فرمول درسراسر خم پیوسته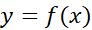
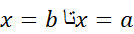 برآوردی از
برآوردی از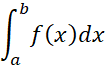 به دست می آید که معمولا برای یک اندازه گام مفروض
به دست می آید که معمولا برای یک اندازه گام مفروض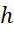 از
از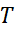 دقیق تر است.
دقیق تر است.
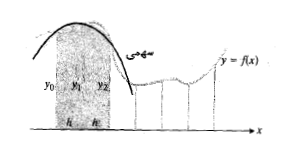
فرمول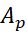 چنین به دست می آید: برای ساده کردن محاسبات جبری، دستگاه مختصات نشان داده شده در شکل زیر را به کار می بریم.
چنین به دست می آید: برای ساده کردن محاسبات جبری، دستگاه مختصات نشان داده شده در شکل زیر را به کار می بریم.
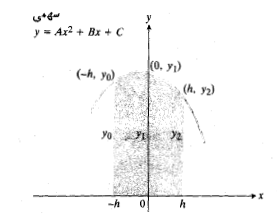
اگر مقیاس محور قائم ثابت بماند،محل محور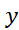 هر جا که باشد مساحت زیر سهمی همواره ثابت می ماند. سهمی معادله ای به صورت زیردارد
هر جا که باشد مساحت زیر سهمی همواره ثابت می ماند. سهمی معادله ای به صورت زیردارد
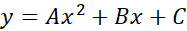
بنابراین مساحت زیر سهمی از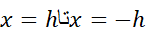 چنین است
چنین است
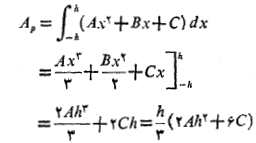
چون خم از سه نقطه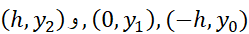 می گذرد داریم
می گذرد داریم
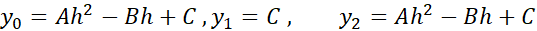
که چنین به دست می آید
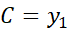
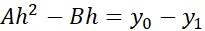
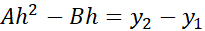
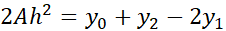
بنابراین، مساحت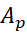 بر حسب مختصهای
بر حسب مختصهای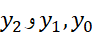 چنین است
چنین است
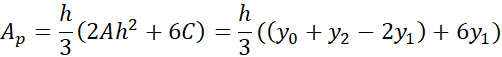
یا
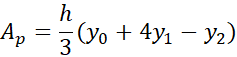
قاعده سیمپسون عبارت است از به کار بردن فرمول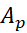 در مورد قطعات متوالی خم
در مورد قطعات متوالی خم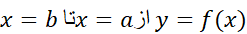 . هر قطعه مجزایی از خم بر زیر بازه ای از
. هر قطعه مجزایی از خم بر زیر بازه ای از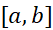 به پهنای
به پهنای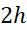 را قوسی از سهمی گذرنده از نقاط انتهایی و میانی زیر بازه تقریب می زند.
را قوسی از سهمی گذرنده از نقاط انتهایی و میانی زیر بازه تقریب می زند.
با افزودن مساحت های زیر قوس های سهمی ها قاعده سیمپسون به دست می آید.

قاعده سیمپسون
برای تقریب زدن
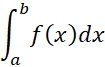
فرمول زیر را به کار می بریم
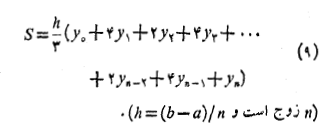
در معادله (9) ،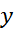 ها مقادیر
ها مقادیر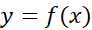 در نقاط
در نقاط
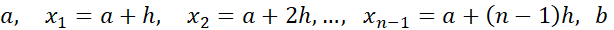
هستند که این نقاط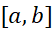 را به
را به 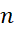 زیر بازه مساوی به طول
زیر بازه مساوی به طول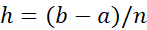 تقسیم می کنند (شکل زیر). چون هر قوس سهموی از دو زیر بازه استفاده می کند، برای به کاربردن این قاعده باید
تقسیم می کنند (شکل زیر). چون هر قوس سهموی از دو زیر بازه استفاده می کند، برای به کاربردن این قاعده باید 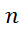 زوج باشد.
زوج باشد.
برآورد خطا در قاعده سیمپسون
برای برآورد کردن خطا در قاعده سیمپسون، با یک نتیجه از حساب دیفرانسیل وانتگرال پیشرفته کار را آغاز می کنیم. این نتیجه حاکی است که اگر مشتق چهارم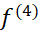 پیوسته باشد،آنگاه برای نقطه ای مانند c بینa و b داریم
پیوسته باشد،آنگاه برای نقطه ای مانند c بینa و b داریم
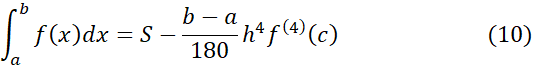
بنابارین وقتی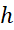
 به سمت صفر میل می کند،خطای
به سمت صفر میل می کند،خطای
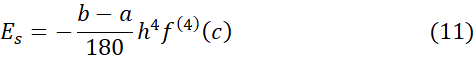
به صورت توان چهارم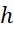
 به سمت صفر میل می کند. ( این مطلب توضیحی است برای اینکهه چرا قاعده سیمپسون احتمالا نتایج بهتری از قاعده ذوزنقه ای به دست می دهد.)
به سمت صفر میل می کند. ( این مطلب توضیحی است برای اینکهه چرا قاعده سیمپسون احتمالا نتایج بهتری از قاعده ذوزنقه ای به دست می دهد.)
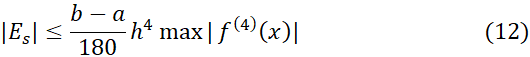
که درآن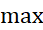 به بازه
به بازه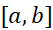 مربوط می شود کران بالایی برای اندازه خطا به دست می دهد. معمولا مقدار دقیق
مربوط می شود کران بالایی برای اندازه خطا به دست می دهد. معمولا مقدار دقیق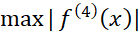 را مانند مقدار
را مانند مقدار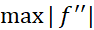 درفرمول خطای قاعده ذوزنقه ای نمی توان به دست آورد و باید به جای آن یک کران بالا قرار داد. اگر
درفرمول خطای قاعده ذوزنقه ای نمی توان به دست آورد و باید به جای آن یک کران بالا قرار داد. اگر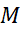 یک کران بالا برای مقادیر
یک کران بالا برای مقادیر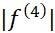 روی بازه
روی بازه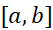 باشد، آنگاه
باشد، آنگاه
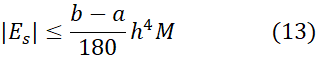
این فرمولی است که معمولا برای برآورد کردن خطا در قاعده سیمپسون به کار می رود. نخست مقدار مناسبی برای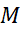 می یابیم و به کمک آن خطای
می یابیم و به کمک آن خطای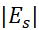 را برآورد می کنیم.
را برآورد می کنیم.
اگر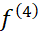 پیوسته و
پیوسته و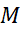 یک کران بالا برای مقادیر
یک کران بالا برای مقادیر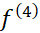 روی بازه
روی بازه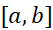 باشد، آنگاه خطای
باشد، آنگاه خطای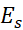 در تقریب زدن انتگرال
در تقریب زدن انتگرال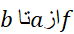 به کمک قاعده سیمپسون، در نابرابری زیر صدق می کند.
به کمک قاعده سیمپسون، در نابرابری زیر صدق می کند.
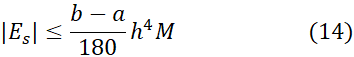
 مثال5 انتگرال زیر را به کمک قاعده سیمپسون با ضابطه
مثال5 انتگرال زیر را به کمک قاعده سیمپسون با ضابطه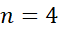 تقریب بزنید
تقریب بزنید
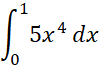
خطای این تقریب زدن را با استفاده از معادله (14) بر آورد کنید.
حل: باز هم انتگرالی را برگزیده ایم که مقدار دقیق آن را می توان مستقینا به دست آورد
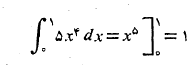
برای یافتن تقریب سیمپسونی اینانتگرال، بازه انتگرال گیری را به چهار زیر بازه تقسیم می کنیم و مقادیر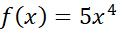 در نقاط انتهایی و نقاط تقسیم را فهرست می کنیم( جدول زیر)
در نقاط انتهایی و نقاط تقسیم را فهرست می کنیم( جدول زیر)
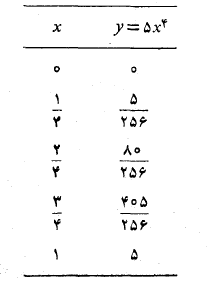
معادله(9) را به ازای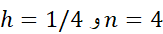 محاسبه می کنیم
محاسبه می کنیم
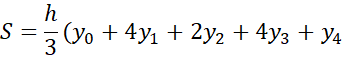
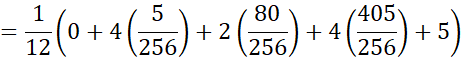
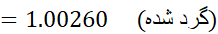
برای برآورد کردن خطا به کمک معادله(14)، نخست یک کران بالا چون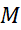 برای مقدار مشتق چهارم
برای مقدار مشتق چهارم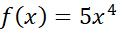 روی بازه
روی بازه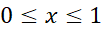 می یابیم. چون مقدارمشتق چهارمثابت و برابر با 120 است، با اطمینان
می یابیم. چون مقدارمشتق چهارمثابت و برابر با 120 است، با اطمینان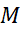 را برابر با 120 بر می گزینیم. بنابراین از معادله (14) به ازای
را برابر با 120 بر می گزینیم. بنابراین از معادله (14) به ازای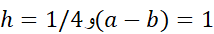 چنین به دست می آوریم
چنین به دست می آوریم
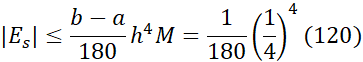
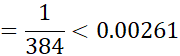
چند جمله ای های از درجه پایین
اگر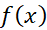 یک چند جمله ای با درجه کمتر از چهار باشد، آنگاه مشتق چهارمش صفر است و داریم
یک چند جمله ای با درجه کمتر از چهار باشد، آنگاه مشتق چهارمش صفر است و داریم
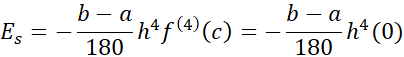
بنابراین در تقریب سیمپسونی هر انتگرالی از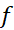
 خطایی وجود ندارد. به دیگر سخن، اگر
خطایی وجود ندارد. به دیگر سخن، اگر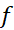
 ثابت، یک تابع درجه اول(خطی) یا یک چند جمله ای درجه دوم یا سوم باشد، صرفنظر از تعداد زیر بازه ها در تقسیم بازه، قاعده سیمپسون مقدار دقیق هر انتگرالی از
ثابت، یک تابع درجه اول(خطی) یا یک چند جمله ای درجه دوم یا سوم باشد، صرفنظر از تعداد زیر بازه ها در تقسیم بازه، قاعده سیمپسون مقدار دقیق هر انتگرالی از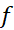
 را به دست می دهد.
را به دست می دهد.
همچنین اگر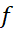 ثابت یا یک تابع درجه اول (خطی) باشد، آنگاه مشتق دومش صفر است و داریم
ثابت یا یک تابع درجه اول (خطی) باشد، آنگاه مشتق دومش صفر است و داریم
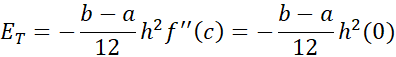
بنابراین، قاعده ذوزنقه ای مقدار دقیق هر انتگرالی از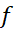 را به دست می دهد. این مطلب عجیب نیست، زیرا در چنین حالاتی ذوزنقه ها کاملا روی نمودار قرار می گیرند.
را به دست می دهد. این مطلب عجیب نیست، زیرا در چنین حالاتی ذوزنقه ها کاملا روی نمودار قرار می گیرند.
 مثال6 انتگرال زیر را به کمک قاعده سیمپسون برآورد کنید
مثال6 انتگرال زیر را به کمک قاعده سیمپسون برآورد کنید
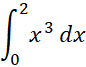
حل: مشتق چهارم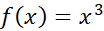 صفر است، بنابراین انتظار می رود قاعده سیمپسون مقدار دقیقانتگرال را با هر تعداد (زوجی) از گام ها به دست دهد. به ازای
صفر است، بنابراین انتظار می رود قاعده سیمپسون مقدار دقیقانتگرال را با هر تعداد (زوجی) از گام ها به دست دهد. به ازای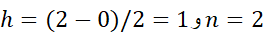 داریم
داریم
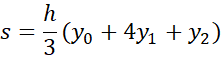
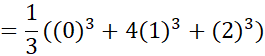
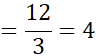
از طرفی داریم
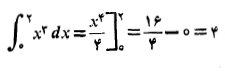
عملیات روی داده های عددی
مثال بعدی چگونگی استفاده از قاعده سیمپسون را در برآورد کردن انتگرال تابعی نشان می دهد که مقادیر آن در آزمایشگاه ی ضمن عمل به دست آمده اند. قاعده ذوزنقه ای را نیز می توان به همین ترتیب به کاربرد.
 مثال 7 شکل زیرباتلاق کوچک شهرکی را نشان می دهد که قرار است زهکشی و سپس پرشود. عمق متوسط باتلاق
مثال 7 شکل زیرباتلاق کوچک شهرکی را نشان می دهد که قرار است زهکشی و سپس پرشود. عمق متوسط باتلاق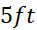 است. پس از اینکه باتلاق زهکشی شد حدود چند یارد مکعب خاک برای پرکردن آن لازم است؟
است. پس از اینکه باتلاق زهکشی شد حدود چند یارد مکعب خاک برای پرکردن آن لازم است؟
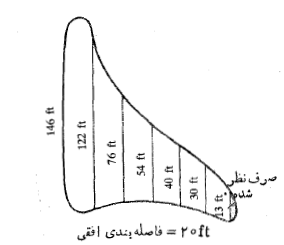
حل: برای محاسبه حجم باتلاق مساحت آن را برآورد، و نتیجه را در 5 ضرب می کنیم. برای برآورد کرد مساحت از قاعده سیمپسون استفاده می کنیم، داریم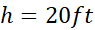 .
. 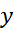 ها طول خطوط قائم در شکل هستند، بنابراین
ها طول خطوط قائم در شکل هستند، بنابراین
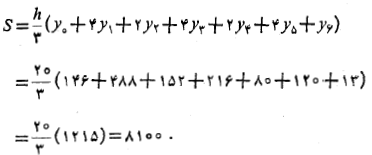
از این رو حجم حدودا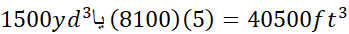 است.
است.
خطاهای ناشی از گرد کردن
گرچه کاستن اندازه گام،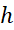 ، از لحاظ نظری خطا را در تقریب های سیمپسونی و ذوزنقه ای کم می کند، اما ممکن است در عمل چنین نباشد. وقتی
، از لحاظ نظری خطا را در تقریب های سیمپسونی و ذوزنقه ای کم می کند، اما ممکن است در عمل چنین نباشد. وقتی
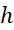 خیلی کوچک باشد، مثلا
خیلی کوچک باشد، مثلا 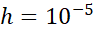 ، خطاهای ناشی از گرد کردن در محاسباتی که برای حساب کردن
، خطاهای ناشی از گرد کردن در محاسباتی که برای حساب کردن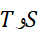 لازم است ممکن است آن قدر جمع شوند که دیگر فرمول خطا نتواند جوابگوی آنچه که پیش می آید باشد.
لازم است ممکن است آن قدر جمع شوند که دیگر فرمول خطا نتواند جوابگوی آنچه که پیش می آید باشد.
اگر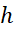 را کمتر از مقدار معینی برگزینیم در عمل ممکن است خطا، به جای اینکه کم شود، بیشتر شود.
را کمتر از مقدار معینی برگزینیم در عمل ممکن است خطا، به جای اینکه کم شود، بیشتر شود.
برای بهره مندی و یادگیری از مباحث بیشتر در این زمینه از محصولکپسول ریاضی عمومی 1در سایت لینوماستفاده کنید.
