صورت های مبهم و قاعده هوپیتال
در اواخر قرن هفدهم، یوهان برتولی برای محاسبهحدکسرهایی که صورت و مخرج شان هر دو به صفر میل می کنند، قاعده ای کشف کرد. امروزه این قاعده را قاعده هوپیتال می نامند. قاعده هوپیتال را می توان به آسانی به کار گرفت، و به سرعت به نتیجه رسید، به ویژه وقتی که روش دیگری وجود ندارد یا کند به نتیجه می رسد.
صورت مبهم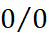
اگر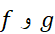 در
در 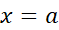 پیوسته باشند، و داشته باشیم
پیوسته باشند، و داشته باشیم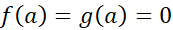 حد
حد 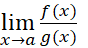 را با قرار دادن
را با قرار دادن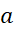 به جای
به جای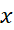 نمی توان به دست آورد، زیرا این کار به
نمی توان به دست آورد، زیرا این کار به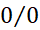 منجر می شود که عبارت بی معنایی است و به آن صورت مبهم می گویند.
منجر می شود که عبارت بی معنایی است و به آن صورت مبهم می گویند.

همانگونه که دیده ایم مقدار حد در معادله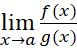 به سادگی قابل پیشگویی نیست؛ مثلا
به سادگی قابل پیشگویی نیست؛ مثلا
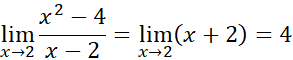
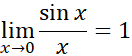
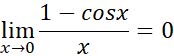
حد
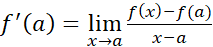
که مشتق از آن محاسبه می شود، همیشه صورت مبهم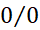 را به دست می دهد. موفقیت در محاسبهمشتق، ما را به این اندیشه وا می دارد که ممکن است با استفاده از مشتق بتوانیم حدهایی را که به صور مبهم می انجامند، پیدا کنیم.
را به دست می دهد. موفقیت در محاسبهمشتق، ما را به این اندیشه وا می دارد که ممکن است با استفاده از مشتق بتوانیم حدهایی را که به صور مبهم می انجامند، پیدا کنیم.
برای مثال:
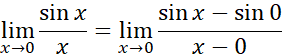
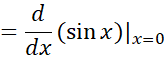

قاعده هوپیتال ارتباط صریح بین مشتق و حدی را که به صورت مبهم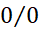 منجر می شود، به دست می دهد.
منجر می شود، به دست می دهد.
قاعده هوپیتال(صورت اول)
فرض کنید که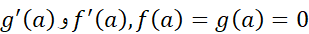 وجود داشته باشند، و
وجود داشته باشند، و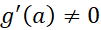 . آنگاه
. آنگاه
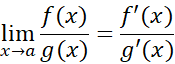
اثبات از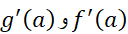 که خودشان هم حد هستند آغاز می کنیم. داریم
که خودشان هم حد هستند آغاز می کنیم. داریم
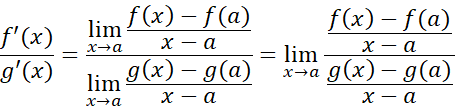
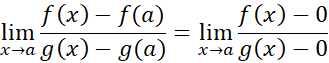
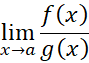
 مثال1
مثال1
الف) 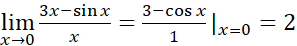
ب) 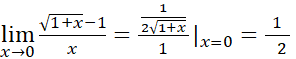
پ) 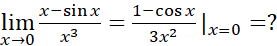
حل:
با حد مورد بحث در مثال1(پ) چه می توان کرد؟ صورت اول قاعده هوپیتال به ما نمی گوید که این حد چیست،زیرا مشتق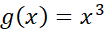 در
در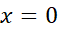 صفر است.
صفر است.
با وجود این صورت قویتری از قاعده هوپیتال هم وجود دارد که می گوید هرگاه قاعده به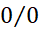 منجر شد می توانیم دوباره از آن استفاده کنیم، و آن قدر این فرایندرا تکرار کنیم که به نتیجه متفاوتی برسیم.
منجر شد می توانیم دوباره از آن استفاده کنیم، و آن قدر این فرایندرا تکرار کنیم که به نتیجه متفاوتی برسیم.
با این قاعده قویار می توانیم کاری را که در مثال1(پ) آغاز کردیم به انجام برسانیم.
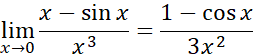
( باز هم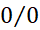 ؛ قاعده را دوباره به کار می بریم.)
؛ قاعده را دوباره به کار می بریم.)
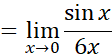
( باز هم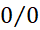 ؛ قاعده را دوباره به کار می بریم.)
؛ قاعده را دوباره به کار می بریم.)
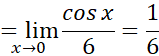
(نتیجه ای متفاوت؛ پایان)
توجه کنید که برای استفاده از قاعده هوپیتال در مورد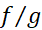 ، مشتق
، مشتق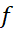 را بر مشتق
را بر مشتق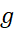 تقسیم می کنیم. کسر مورد استفاده
تقسیم می کنیم. کسر مورد استفاده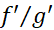 است و نه
است و نه 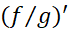 . در دام مشتق گیری
. در دام مشتق گیری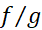 ازنیفتید.
ازنیفتید.
قاعده هوپیتال (صورت قویتر)
فرض کنید 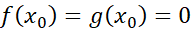 و توابع
و توابع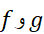 هر دو بر بازه باز
هر دو بر بازه باز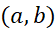 ، که نقطه
، که نقطه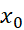 را در بر دارد، مشتق پذیر باشند. و نیز فرض کنید در هر نقطه از
را در بر دارد، مشتق پذیر باشند. و نیز فرض کنید در هر نقطه از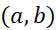 بجز احتمالا در
بجز احتمالا در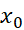 ،
،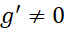 .آنگاه با این شرط که حد طرف راست معادله زیروجود داشته باشد، داریم
.آنگاه با این شرط که حد طرف راست معادله زیروجود داشته باشد، داریم
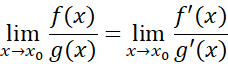
اثبات صورت قویتر قاعده هوپیتال مبتنی بر شکل خاصی ازقضیه مقدار میانگین است.
 مثال2
مثال2
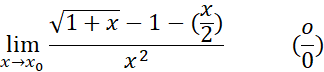
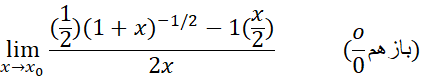
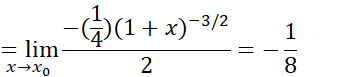
هنگام استفاده از قاعده هوپیتال در پی این باشید که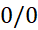 به مقدار دیگری تبدیل شود. از اینجا مقدار حد معلوم می شود.
به مقدار دیگری تبدیل شود. از اینجا مقدار حد معلوم می شود.
 مثال 3
مثال 3
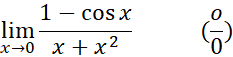
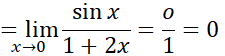
اگر باز هممشتق بگیریم و قاعده هوپیتال را بار دیگر به کار ببریم، خواهیم داشت
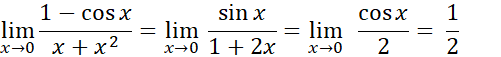
که غلط است.
اگر به جایی برسیم که یکی از مشتق ها صفر و دیگری ناصفر باشد، آنگاه حد کورد نظر یا نظیر مثال 3، صفر، یا نظیر مثال زیر بینهایت است.
 مثال 4
مثال 4
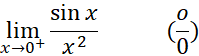
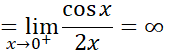
صورت های مبهم دیگر
در کتاب های پیشرفته تر، ثابت می کنند که قاعده هوپیتال نه تنها در مورد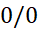 بلکه در مورد صورت مبهم
بلکه در مورد صورت مبهم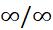 نیز به کار می رود.
نیز به کار می رود.
اگر وقتی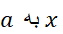 میل می کند،
میل می کند،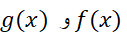 هر دو بهبینهایت میل کنند، آنگاه با این شرط که حد سمت راست تساوی زیر وجود داشته باشد، داریم
هر دو بهبینهایت میل کنند، آنگاه با این شرط که حد سمت راست تساوی زیر وجود داشته باشد، داریم
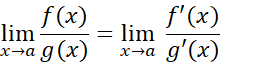
در نماد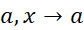 می تواند متناهی یا نامتناهی باشد.
می تواند متناهی یا نامتناهی باشد.
 مثال 5
مثال 5
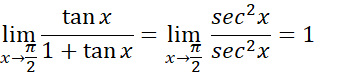
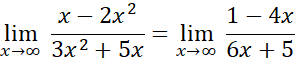
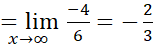
صورت های 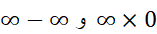 را هم گاه می توان با تغییر دادن عبارات به کمک عملیات جبری به صورت
را هم گاه می توان با تغییر دادن عبارات به کمک عملیات جبری به صورت 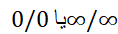 تبدیل کرد. ( در اینجا با زهم نمی خواهیم القا کنیم که عددی چون
تبدیل کرد. ( در اینجا با زهم نمی خواهیم القا کنیم که عددی چون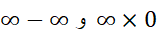 وجود دارد؛ همان طور که در مورد
وجود دارد؛ همان طور که در مورد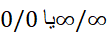 هم قصد ما این نبود. این صورت ها عدد نیستند، بلکه توصیف کننده حدهایی هستند.)
هم قصد ما این نبود. این صورت ها عدد نیستند، بلکه توصیف کننده حدهایی هستند.)

 مثال6
مثال6
حد 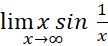
به صورت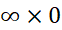 منجر می شود، اما با نوشتن
منجر می شود، اما با نوشتن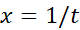 و میل دادن
و میل دادن 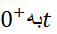 ، می توانیم آن را به صورت
، می توانیم آن را به صورت 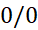 تبدیل کنیم.
تبدیل کنیم.
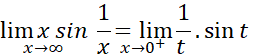
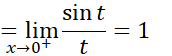
 مثال 7 مطلوب است
مثال 7 مطلوب است
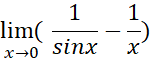
حل: اگر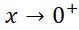 ، آنگاه
، آنگاه 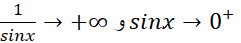 ، حال آنکه
، حال آنکه 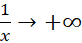 . عبارت
. عبارت 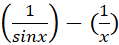 رسما به صورت
رسما به صورت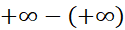 در می آید که مبهم است.از طرف دیگر اگر
در می آید که مبهم است.از طرف دیگر اگر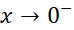 ، آنگاه
، آنگاه 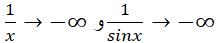 ، لذا
، لذا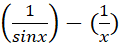 به صورت
به صورت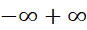 در می آید که این هم مبهم است. اما داریم
در می آید که این هم مبهم است. اما داریم
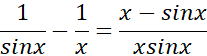
حال قاعده هوپیتال را در مورد عبارت سمت راست به کار می بریم
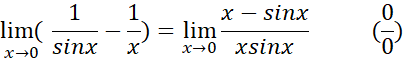
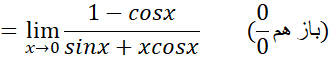
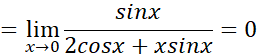
چه هنگام از قاعده هوپیتال استفاده کنیم و چه هنگام دست نگه داریم
برای یافتن
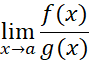
با استفاده از قاعده هوپیتال، به مشتق گرفتن از 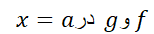 مادام که صورت
مادام که صورت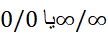 بدست می آید ادامه دهید. به محض اینکه به چیز دیگری رسیدید مشتق گیری را متوقف سازید. وقتی هریک از صورت یا مخرج،حد نا صفر متناهی داشته باشد، قاعده هوپیتال کاربرد ندارد.
بدست می آید ادامه دهید. به محض اینکه به چیز دیگری رسیدید مشتق گیری را متوقف سازید. وقتی هریک از صورت یا مخرج،حد نا صفر متناهی داشته باشد، قاعده هوپیتال کاربرد ندارد.
تقریب های درجه دوم و خطاهای تقریب:
تعمیم قضیه مقدار میانگین(صورت اول)
صورت مختصرا تغییر یافتهقضیه مقدار میانگین این است که اگر تابعی چون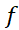 در هر نقطه از بازه بسته
در هر نقطه از بازه بسته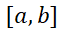 پیوسته و در هر نقطه از بازه باز(
پیوسته و در هر نقطه از بازه باز(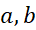 ) مشتق پذیر باشد،آنگاه دست کم یک عدد چون
) مشتق پذیر باشد،آنگاه دست کم یک عدد چون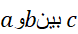 وجود دارد که در آن
وجود دارد که در آن
(1 الف) 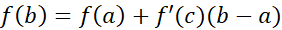
اگر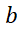 را یک متغیر مستقل در نظر بگیریم، می توانیم معادله(1الف) را به صورت
را یک متغیر مستقل در نظر بگیریم، می توانیم معادله(1الف) را به صورت
(1 ب) 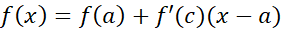
بنویسیم که برای بازه از 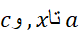 یی در بین آن ها، درست است. طرف راست معادله (1ب) شبیه صورت خطی
یی در بین آن ها، درست است. طرف راست معادله (1ب) شبیه صورت خطی
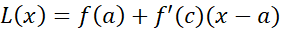
است. همان گونه که قضیه زیر نشان می دهد این تشابه تصادفی نیست.
قضیه 6
تعمیم قضیه مقدار میانگین (صورت اول)
اگرf'وf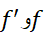 در هر نقطه از
در هر نقطه از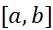 پیوسته، و
پیوسته، و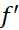 در هر نقطه از (
در هر نقطه از (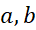 ) مشتق پذیر باشد، آنگاه دست کم یک عدد چون
) مشتق پذیر باشد، آنگاه دست کم یک عدد چون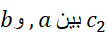 وجود دارد به قسمی که
وجود دارد به قسمی که
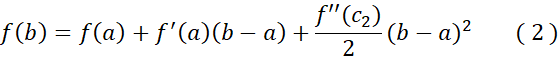
اهمیت معادله 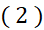 در این نیست که عددی چون
در این نیست که عددی چون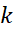 در
در
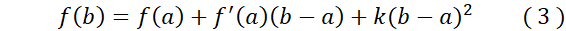
صدق می کند. اطلاع از وجود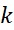 اطلاع چندان تازه ای نیست زیرا از معادله
اطلاع چندان تازه ای نیست زیرا از معادله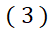 همواره می توان آن را به دست آورد. اهمیت معادله
همواره می توان آن را به دست آورد. اهمیت معادله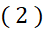 در این است که به ازای نقطه ای بینkمقدار
در این است که به ازای نقطه ای بینkمقدار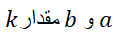 نصف مقدار
نصف مقدار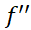 است. این مطلب حاکی است که
است. این مطلب حاکی است که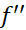 اندازه
اندازه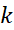 را کنترل می کند.
را کنترل می کند.
به زودی خواهیم دید که این اطلاع تا چه اندازه می تواند مفید باشد.
اثبات معادله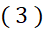 حاکی است که وقتی
حاکی است که وقتی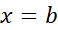 ، مقدار تابع
، مقدار تابع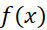 ، و تابع
، و تابع 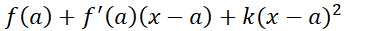
یکی خواهد بود. این دو تابع در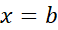 هم مقدار مساوی خواهند داشت (این مقدار
هم مقدار مساوی خواهند داشت (این مقدار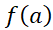 است)، اما عموما اختلافشان
است)، اما عموما اختلافشان
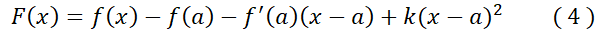
صفر نیست.
تابع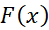 بر بازه
بر بازه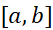 در تمام فرض های قضیه رول صدق می کند:
در تمام فرض های قضیه رول صدق می کند: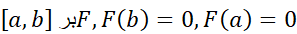 پیوسته است زیرا
پیوسته است زیرا
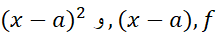 پیوسته اند، وبه دلیل مشابه،
پیوسته اند، وبه دلیل مشابه،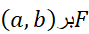 مشتق پذیر است. پس به ازای نقطه ای چون
مشتق پذیر است. پس به ازای نقطه ای چون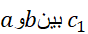 داریم
داریم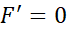 :
:

چون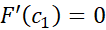 ، مشتق
، مشتق
(5) 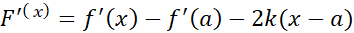
بر بازه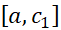 در تمام فرض های قضیه رول صدق می کند:
در تمام فرض های قضیه رول صدق می کند: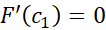 و اگر در معادله (5) به جایa,x
و اگر در معادله (5) به جایa,x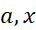 را قرار دهیم داریم
را قرار دهیم داریم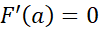
همچنین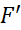 بر
بر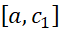 پیوسته و بر
پیوسته و بر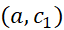 مشتق پذیر است، زیرا
مشتق پذیر است، زیرا 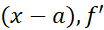 هر دوچنین اند. بنابراین، مشتق
هر دوچنین اند. بنابراین، مشتق 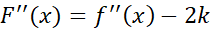
در نقطه ای چون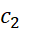 ,
,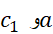 صفر است، و این بدین معناست که
صفر است، و این بدین معناست که 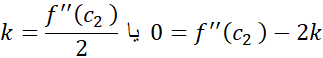
اگر در معادله (3) به جای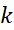 این مقدار را قرار دهیم معادله (2) به دست می آید که مطلوب ما است.
این مقدار را قرار دهیم معادله (2) به دست می آید که مطلوب ما است.
نکتهاین قضیه و اثبات آن با فرض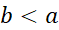 هم صادق اند، با این شرط که به جای ذکر صریح
هم صادق اند، با این شرط که به جای ذکر صریح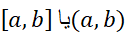 قید کنیم « بازه با نقاط انتهایی
قید کنیم « بازه با نقاط انتهایی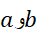 ». اگر در مورد این بازه و سایر بازه هایی که در اثبات مطرح می شوند چنین کنیم، استدلال را می توان به درستی به انجام رساند.
». اگر در مورد این بازه و سایر بازه هایی که در اثبات مطرح می شوند چنین کنیم، استدلال را می توان به درستی به انجام رساند.

اندازه گیری خطا در یک تقریب خطی
حال در موقعیتی هستیم که خطای تقریب خطی
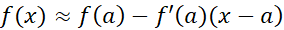
را محاسبه می کنیم. در آغاز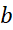 را یک متغیر مستقل تلقی می کنیم، و معادله (2) را با آگاهی از اینکه
را یک متغیر مستقل تلقی می کنیم، و معادله (2) را با آگاهی از اینکه 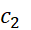 بین
بین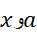 قرار دارد به صورت
قرار دارد به صورت
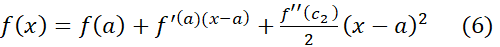
می نویسیم. این معادله، باتوجه به نکته مذکور در پایان اثبات قضیه،هم برای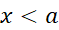 بر قرار است و هم برای
بر قرار است و هم برای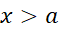 .
.
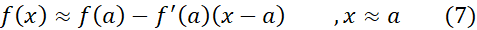
به دست می آید که بر بازه با دو انتهای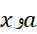 درست است، وخطایش برابر است با
درست است، وخطایش برابر است با
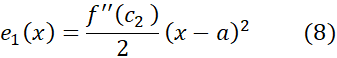
اگر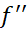 بر بازه بسته از
بر بازه بسته از 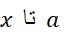 پیوسته باشد، آنگاه بر این بازه یک مقدار ماکسیمم دارد، و
پیوسته باشد، آنگاه بر این بازه یک مقدار ماکسیمم دارد، و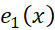 در نابرابری
در نابرابری
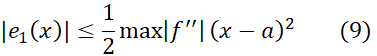
صدق می کند. در اینجا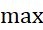 مربوز است به بازه با دو انتهای
مربوز است به بازه با دو انتهای 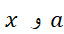 . اما، وقتی برای برآورد خطا از این نابرابری استفاده می کنیم، معمولا نمی توانیم مقدار دقیق'
. اما، وقتی برای برآورد خطا از این نابرابری استفاده می کنیم، معمولا نمی توانیم مقدار دقیق'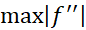 را بیابیم، و مجبوریم به جای آن یک کران بالا یا مقدار«حالت بدتر» را قرار دهیم.
را بیابیم، و مجبوریم به جای آن یک کران بالا یا مقدار«حالت بدتر» را قرار دهیم.
اگرM کران بالای دلخواهی از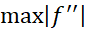 باشد، آنگاه
باشد، آنگاه
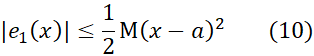
این نابرابری همان است که معمولا برای برآورد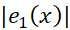 از آن استفاده می شود. ما بهترین M را که می توانیم، پیدا می کنیم و کار را ادامه می دهیم. برای اینکه به ازای یکM مفروض،
از آن استفاده می شود. ما بهترین M را که می توانیم، پیدا می کنیم و کار را ادامه می دهیم. برای اینکه به ازای یکM مفروض،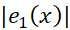 را کوچک کنیم، صرفا
را کوچک کنیم، صرفا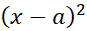 را کوچک می کنیم.
را کوچک می کنیم.
خطا در تقریب خطی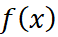 در نزدیکی
در نزدیکی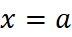
اگر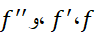 در هر نقطه از بازه بسته ای با دو انتهای
در هر نقطه از بازه بسته ای با دو انتهای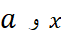 پیوسته باشند، آنگاه در این بازه خطای
پیوسته باشند، آنگاه در این بازه خطای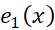 ناشی از قرار دادن صورت خطی
ناشی از قرار دادن صورت خطی
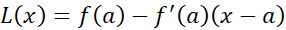
به جای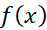 ،، در نابرابری
،، در نابرابری
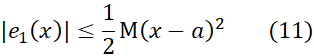
صدق می کند. در اینجاM کران بالای دلخواهی است برای مقادیر'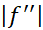 بر بازه با دو انتهای
بر بازه با دو انتهای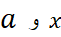 .
.
 مثال1 صورت خطی
مثال1 صورت خطی 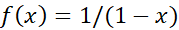 در
در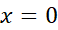 عبارت است از
عبارت است از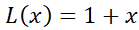 . اگر
. اگر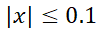 ، تقریب
، تقریب 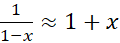 تا چه حد خوب است؟
تا چه حد خوب است؟
حل: از نابرابری (11) برای یافتن یک کران بالا برای 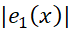 ، به ازای
، به ازای 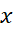 مفروض، استفاده می کنیم. ابتدامشتق دوم
مفروض، استفاده می کنیم. ابتدامشتق دوم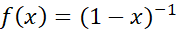 را پیدا می کنیم.
را پیدا می کنیم.
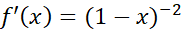 ،
،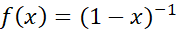
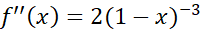
حال برای مقادیر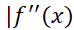 بر بازه
بر بازه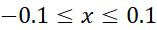 کران بالایی چون
کران بالایی چون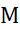 می یابیم. براین بازه داریم
می یابیم. براین بازه داریم
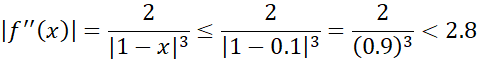
می توانیم با اطمینان کامل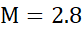 را در نظر بگیریم. با این مقدار
را در نظر بگیریم. با این مقدار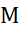 و با
و با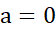 ، از نا برابری (11)نتیجه می گیریم که
، از نا برابری (11)نتیجه می گیریم که
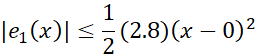
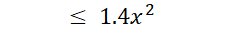
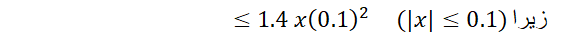
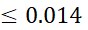
در تقریب 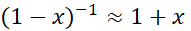 اگر
اگر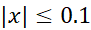 ، خطا بیش از 0.014نیست.
، خطا بیش از 0.014نیست.
تقریب درجه دوم
برای اینکه تقریب خطی از دقت بیشتری برخوردار باشد، یک جمله درجه دوم هم به ان اضافه می کنیم. چند تقریب درجه دوم معمولی در نزدیکی0 این ها هستند.
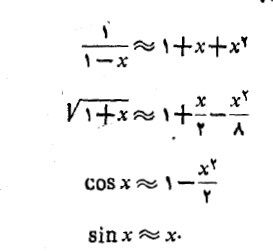
تقریب های دیگر را می توان با کمک جبر از این ها به دست آورد. برای 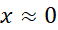 داریم
داریم
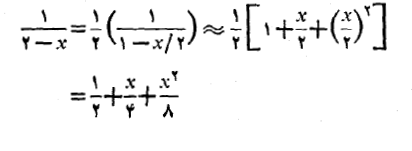
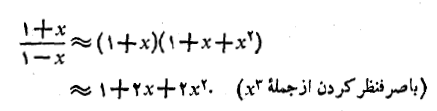
برای اینکه تقریب ها را به طور صحیح با هم ترکیب کنیم، هریک از آن ها در وقت کاربرد باید معتبر باشد
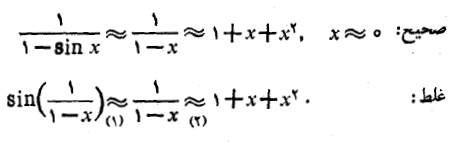
ترکیب دوم غلط است زیرا تقریب (1) ایجاب می کند که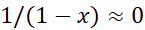 ، و لذا
، و لذا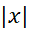 بزرگ باشد؛ حال آنکه تقریب(2) ایجاب می کند که
بزرگ باشد؛ حال آنکه تقریب(2) ایجاب می کند که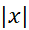 کوچک باشد.
کوچک باشد.
اگر قضیه مقدار میانگین را به طریق زیر باز هم تعمیم دهیم، می توانیم برآورد خوبی از خطای تقریب های درجه دوم به دست آوریم.
قضیه 7
تعمیم قضیه مقدار میانگین (صورت دوم)
اگر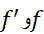 و
و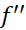 بر
بر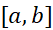 پیوسته باشند و
پیوسته باشند و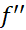 بر (
بر (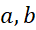 ) مشتق پذیر هم باشد، آنگاه عددی چون
) مشتق پذیر هم باشد، آنگاه عددی چون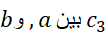 وجود دارد که به ازای آن
وجود دارد که به ازای آن
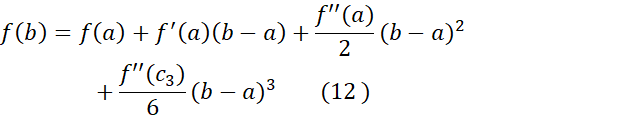
اثبات تعمیم اخیر قضیه مقدار میانگین، که شبیه اثبات تعمیم قبلی آن است، حالت خاصی است.
در کاربردها معمولا در معادله (12) به جایx, b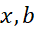 را می نویسیم
را می نویسیم

با آگاهی از اینکه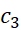 بین
بین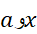 واقع است. ازمعادله(13) تقریب درجه دوم
واقع است. ازمعادله(13) تقریب درجه دوم
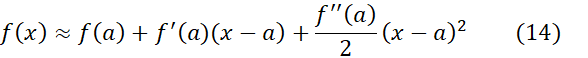
را به دست می آوریم که بر بازه بین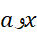 معتبر است، و خطای آن چنین است
معتبر است، و خطای آن چنین است
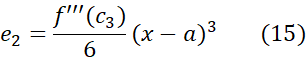
توجه کنید که دو جمله اول موجود در طرف راست تقریب(14)، تقریب خطی متداول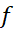 را به دست می دهد. برای به دست آوردن تقریب درجه دوم تنها باید جمله درجه دوم را، بدون تغییر قسمت خطی، به آن بیفزاییم.
را به دست می دهد. برای به دست آوردن تقریب درجه دوم تنها باید جمله درجه دوم را، بدون تغییر قسمت خطی، به آن بیفزاییم.
اگر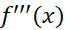 بر بازه بسته از
بر بازه بسته از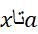 پیوسته باشد،آنگاه بر آن بازه یک مقدارماکسیمم دارد، و بنا به معادله(15) داریم
پیوسته باشد،آنگاه بر آن بازه یک مقدارماکسیمم دارد، و بنا به معادله(15) داریم
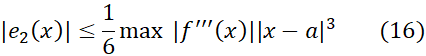
بخت ما در یافتن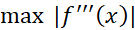 بیش از یافتن
بیش از یافتن 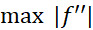 نیست؛ و لذا به جای آن یک کران بالا مانند
نیست؛ و لذا به جای آن یک کران بالا مانند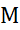 می گذاریم،و
می گذاریم،و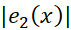 را با نابرابری
را با نابرابری
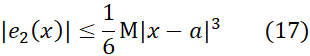
بر آورد می کنیم.
تقریب درجه دوم 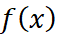 در نزدیکی
در نزدیکی 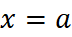
اگر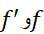 و
و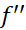 و
و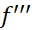 در هر نقطه از بازه بسته ای با دو انتهای
در هر نقطه از بازه بسته ای با دو انتهای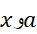 پیوسته باشند، آنگاه در این بازه خطای
پیوسته باشند، آنگاه در این بازه خطای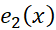 ناشی از قرار دادن تقریب درجه دوم
ناشی از قرار دادن تقریب درجه دوم
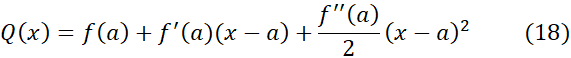
به جای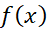 ، در نابرابری
، در نابرابری
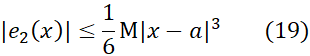
صدق می کند. در اینجاM کران بالای دلخواهی است برای مقادیر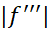 بر بازه با دو انتهای
بر بازه با دو انتهای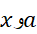 .
.
 مثال 2 تقریب درجه دوم
مثال 2 تقریب درجه دوم 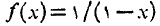 را در نزدیکی
را در نزدیکی 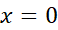 بیابید. اگر
بیابید. اگر 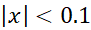 ، این تقریب چقدر دقیق است؟
، این تقریب چقدر دقیق است؟
حل: برای یافتن تقریب درجه دوم، از معادله (18) با ضابطه 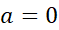 استفاده می کنیم.
استفاده می کنیم.
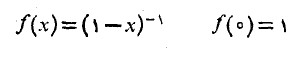
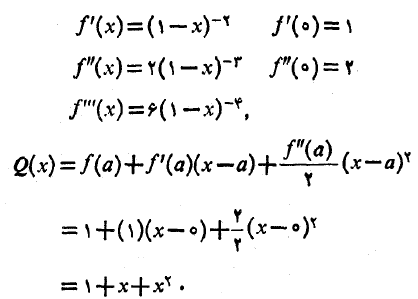
تقریب درجه دوم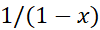 در نزدیکی
در نزدیکی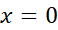 عبارت است از
عبارت است از
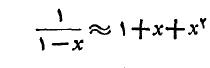
برای برآورد خطای تقریب، ابتدایک کران بالا چون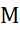 برای مقادیر
برای مقادیر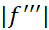 در بازه
در بازه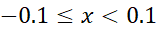 می یابیم. در این بازه،
می یابیم. در این بازه،
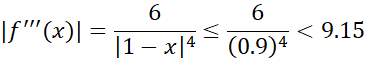
لذا با اطمینان می توانیم بنویسیم 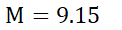 . حال از نابرابری (19) با ضوابط
. حال از نابرابری (19) با ضوابط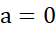 و
و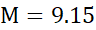 استفاده می کنیم.
استفاده می کنیم.
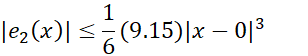
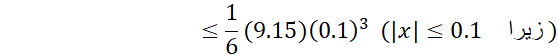
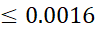
اگر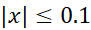 ، خطای تقریب بیش از 0.0016نیست. در مقایسه با کران بالای0.014 که در مثال1 برای تقریب خطی
، خطای تقریب بیش از 0.0016نیست. در مقایسه با کران بالای0.014 که در مثال1 برای تقریب خطی 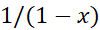 یافتیم، مقدار0.0016 بهتر است.
یافتیم، مقدار0.0016 بهتر است.
 مثال 3تقریب درجه دوم
مثال 3تقریب درجه دوم 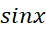 را در نزدیکی
را در نزدیکی 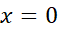 بیابید. برای خطای تقریب بر بازه
بیابید. برای خطای تقریب بر بازه 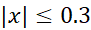 ، یک کران بالا پیدا کنید.
، یک کران بالا پیدا کنید.
حل: برای یافتن تقریب درجه دوم، از معادله(18) با ضوابط 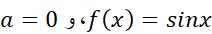 استفاده می کنیم:
استفاده می کنیم:
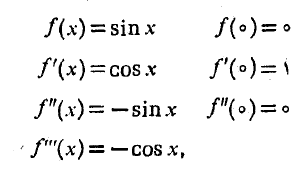
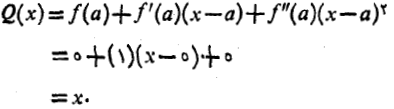
تقریب درجه دوم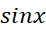 در نزدیکی
در نزدیکی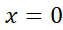 عبارت است از
عبارت است از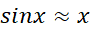 .
.
این تقریب که در آن جمله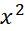 وجود ندارد چگونه می تواند در جه دوم باشد؟ در این تقریب جمله درجه دوم وجود دارد، اما ضریبش صفر است. مهم این است که از جمله درجه دوم صرف نظر نشده است، و می توانیم خطای تقریب را به جای
وجود ندارد چگونه می تواند در جه دوم باشد؟ در این تقریب جمله درجه دوم وجود دارد، اما ضریبش صفر است. مهم این است که از جمله درجه دوم صرف نظر نشده است، و می توانیم خطای تقریب را به جای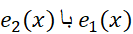 برآورد کنیم.
برآورد کنیم.
برای یافتن یک کران بالا برای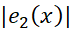 بر بازه
بر بازه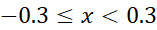 ، ابتدا یک کران بالا برای
، ابتدا یک کران بالا برای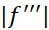 می یابیم. چون
می یابیم. چون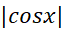 هرگز از 1 بیشتر نمی شود، داریم:
هرگز از 1 بیشتر نمی شود، داریم:
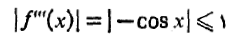
با اطمینان می نویسیم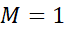 . با ضوابط
. با ضوابط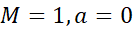 ، نابرابری (19) نتایج زیر را به دست می دهد.
، نابرابری (19) نتایج زیر را به دست می دهد.
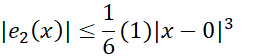
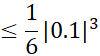
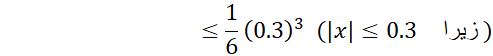
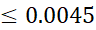
خطا در بازه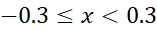 هرگز از
هرگز از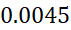 بیشتر نمی شود.
بیشتر نمی شود.
برای مطالعه مباحث بیشتر در این زمینه از محصول کپسول آموزشی ریاضی عمومی 1 سایتلینوم استفاده کنید.