تابع های متعالی

اگر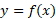 اندازه کمیتی باشد که با زمان تغییر می کند، آنگاه معادله 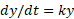یا

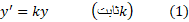
حاکی است که در هر لحظه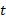،آهنگ تغییر 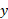متناسب است با مقدار 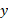موجود. بسته به تابع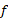، این آهنگ ممکن است تغییرات گوناگونی را توصیف کند. از جمله : اتلاف حرارت جسمی که به یک محیط خنک کننده وارد می شود ( نقره داغی که در آب فرو می رود)، تغییر جریان در یک مدار الکتریکی که با باتری کار می کند، یا فروپاشی یک عنصر رادیو اکتیو مثل کربن 14( تعدا اتمهایی که در هر واحد زمان تجزیه می شود متناسب است با تعداد اتم های رادیواکتیوی که باقی می ماند).

در این مقاله خواهیم دید که یکی از جواب های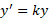 تابع نمایی

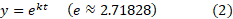
است که یکی از توابع موسوم به توابع متعالی است. امروزه تابعی چون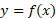 را متعالی نامند اگر در معادله به صورت

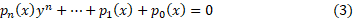
که در آن ضرایب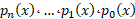  چند جمله ای هایی بر حسب 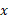اند، صدق نکند. تابعی که در معادله ای نظیر (3) صدق کند، جبری نام دارد. مثلا، 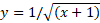جبری است زیرا در معادله  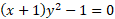صدق می کند. در اینجا ضرایب عبارت اند از چند جمله ای های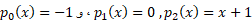. چند جمله ای ها، و توابع گویا جبری هستند. تمام خاصل جمع ها، حاصل ضرب ها، خارج قسمت ها، توان ها، و ریشه های توابع جبری نیز جبری اند.  شش تابع اصلی مثلثاتی، متعالی اند. توابع مثلثاتی معکوس، و توابع و لگاریتمی هم که موضوع اصلی این مقاله اند متعالی هستند.

تابع های معکوس یکدیگر

برای پیگیری مبحث حساب دیفرانسیل و انتگرال لازم است توابعی را تعریف کنیم که به بهترین وجه به صورت معکوس توابعی که تاکنون دیده ایم معرفی می شوند. در این مقاله درباره اینکه دو تابع به چه مفهومی معکوس یکدیگرند بحث می کنیم، و از اینجا نتایجی در مورد فرمول ها، نمودارها و مشتقات آن ها به دست می آوریم.

تابع های یک به یک معکوس دارند

تابع قاعده ای است که به هر عدد در دامنه اش عددی از بردش را تخصیص می دهد. توابعی نظیر 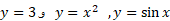  می توانند به ازای ورودی های متفاوت خروجی یکسان داشته باشند. ولی توابعی نظیر

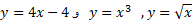
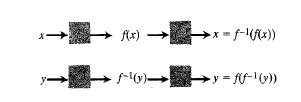
همواره به ازای ورودی های متفاوت خروجی های مختلف دارند. توابعی را که به ازای ورودی های مختلف همیشه خروجی های مختلف دارند، توابع یک به یک می نامند. چون خروجی یک تابع یک به یک از فقط یک ورودی به دست می آید، هر تابع یک به یک را می توان معکوس کرد تا خروجی ها را به ورودی های مربوط برگرداند شکل زیر.

تابعی که از معکوس کردن یک تابع یک به یک به دست می آید معکوس نام دارد. نماد معکوس، 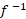است. نماد 1- در 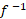نما نیست: یعنی 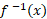برابر با 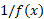نیست.

همانگونه که در شکل زیر دیده می شود، نتیجه ترکیب 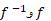، به هر ترتیب که باشد، تابع همانی است. تابع همانی تابعی است که به هر عدد همان عدد را نسبت می دهد. آزمون اینکه دو تابع 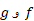معکوس یکدیگر هستند یا نه، به این صورت است: 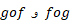را نحاسبه می کنیم، اگر هر دو ترکیب تابع همانی باشند، آنگاه 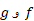معکوس یکدیگراند، و در غیر این صورت چنین نیست.

چه توابعی معکوس دارند؟ توابع صعودی و توابع نزولی معکوس دارند، زیرا یک به یک اند. در بینتوابع پیوسته، این ها تنها توابعی هستند که معکوس دارند، اما ما به اثبات این مطلب نمی پردازیم.

نمودار تابع های معکوس

نمودار معکوس یک تابع چه ارتباطی با نمودار خود تابع دارد؟ فرضا اگر تابع صعودی باشد، نمودارش نظیر نمودار موجود در شکل زیر از چپ به راست خیز بر می دارد.

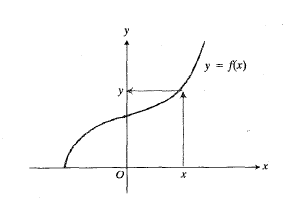
برای خواندن نموار، با نقطه واقع بر محور آغاز می کنیم، به بالا می رویم تا به نمودار برسیم، و سپس به محور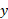 می رویم تا مقدار 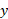را بیابیم. اگر از 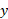آغاز کنیم و بخواهیم 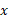مربوط به 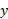را بیابیم، بر عکس عمل می کنیم همانند شکل

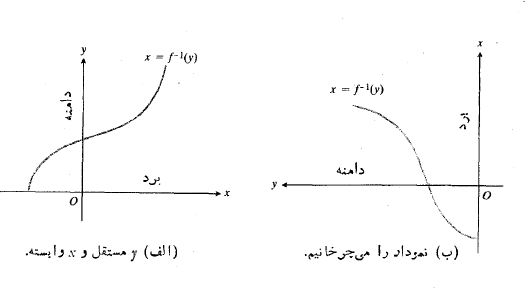
نمودار همان نمودار است که بر خلاف معمول محور دامنه افقی و محور برد قائم رسم نشده است. برای رسم نمودار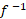 به طوری که مطابق با عادت ما باشد، باید با روش زیر آن را از نمودار 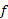به دست آوریم. نمودار 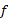شکل زیر قسمت (الف) را در خلاف جهت ساعت میچرخانیم تا محور 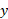افقی، و محور 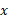قائم شود همانند شکل زیر قسمت (ب). سپس قرینه نمودار را نسبت به محور قائم چنان می یابیم که گویی این محور آینه ای است که جهت محور 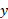را از چپ به راست بر می گرداند قسمت (پ) شکل. در پایان به جای 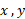و به جای 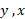می نویسیم قسمت (ت) شکل. بدین ترتیب نمودار معمولی 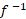به صورت تابعی از 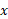به دست می آید.

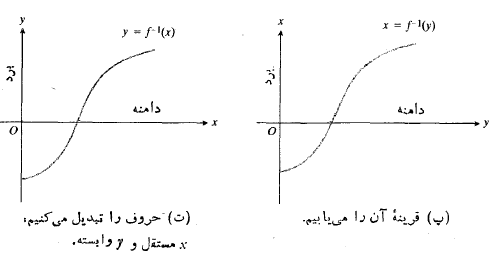
حال به ارتباط نمودار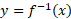 با نمودار 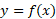پی بردیم، می توانیم آن را به روش سریع تری رسم کنیم. برای رسیدن به قسمت (ت) و (الف) شکل، معادله 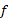را نسبت به 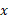و بر حسب  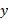حل، و جای  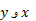را با یکدیگر عوض می کنیم. اثر این کار دقیقا مانند این است که قرینه نمودار  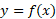را نسبت به خط  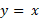بیابیم.

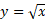مثال1  معکوس تابع، را به صورت تابعی از 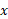بیابید. سپس نمودار 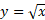و نمودار معکوسش را با هم رسم کنید.

حل: از معادله 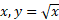 را بر حسب 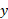محاسبه می کنیم، و حروف 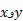را به هم تبدیل می کنیم

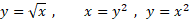
معکوس تابع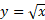، تابع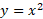، 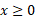است. محدودیت 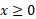که در برد  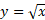نهفته است، باید برای دامنه تابع معکوس 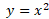منظور شود، زیرا دامنه بدون محدودیت به صورت 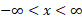است که قابل قبول نیست. برای آزمایش می نویسیم

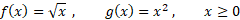
و می بینیم که ترکیب، به هر ترتیب که باشد، تابع همانی است

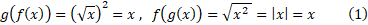
در معادله آخر می توانیم از نماد قدر مطلق صرف نظر کنیم، زیرا .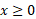

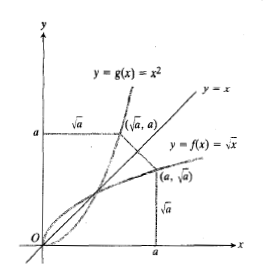
اگر نمودار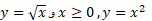 را یک جا رسم کنیم همانند شکل، تقارن دو تابع نسبت به خط 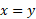مشخص می شود. نمودار 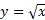از نقاط 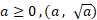تشکیل می شود. حال آنکه نمودار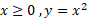، متشکل از نقاط  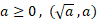است.

نکته معادلا (1) نشان می دهند که تابع 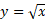، معکوس تابع است. هر تابع یک به یک، معکوس معکوس خود است

مثال2 معکوس تابع زیر را بیابید

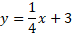
حل: از معادله مفروض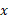 را بر حسب 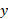به دست می آوریم

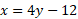
حال در معادله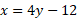 جای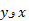 را عوض می کنیم و 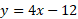را به دست می آوریم. معکوس 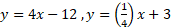است. برای آزمایش، می نویسیم

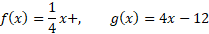
پس

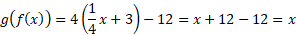
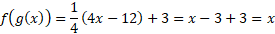
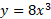مثال3 معکوس تابع را بیابید.

حل: از معادله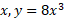 را بر حسب 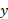به دست می آوریم

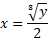
با تعویض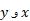 داریم

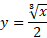
معکوس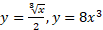 است. برای آزمودن محاسبات، ترکیب های این دو تابع را به دست می آوریم تا مطمئن شویم که هریک از ترکیب ها تابع همانی است

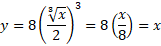
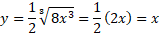
مشتق معکوس یکتابع مشتق پذیر

اگر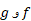 معکوس یکدیگر باشند، نمودارهایشان، نظیر شکل زیر تصویر آینه ای یکدیگر نسبت به خط 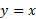اند. پس اگر 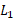خط مماس بر نمودا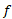ردر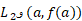 تصویر آینه ای 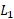نسبت به خط  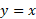باشد، طبیعی است که انتظار داشته باشیم  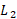مماس بر نمودار 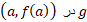باشد. چون نسبت خیز 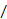رو بر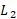 متناظر با نسبت رو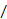خیز بر 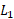است، می بینیم که شیب خط 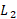یعنی 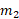 عکس شیب خط  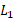یعنی 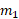 است.

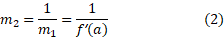
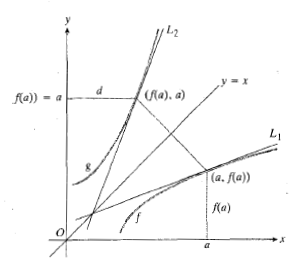
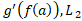اگر واقعا مماس بر نمودار باشد، آنگاه شیباست و داریم

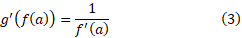
قاعده محاسبه مشتق معکوس یک تابع مشتق پذیر به شرح زیر است.

قاعده 11

قاعده محاسبه مشتق تابع های معکوس

اگر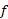 در هر نقطه از یک بازه  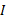مشتق پذیر باشد، و 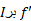هرگز صفر نشود، آنگاه 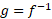در هر نقطه داخلی بازه 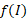مشتق پذیر است، و مقدار آن در نقطه 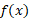برابر است با

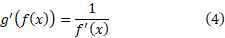
در یکی از نتایجقضیه مقدار میانگین نشان دادیم که اگر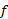 در هر نقطه از یک بازه باز 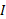مشتق پذیر باشد، واگر 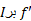هرگز صفر نشود، آنگاه  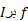یک به یک است. چنین تابعی مسلما معکوس دارد. قاعده 11 حاکی است که 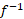نیز مشتق پذیر است و مشتق آن عکس مشتق 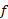است، و از معادله (4) به دست می آید.

در بحث درباره قاعده زنجیری در مورد معادلات گفتیم که اگر مشتق 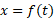 بر بازه ای چون  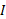هرگز صفر نشود، آنگاه معادله  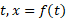را  به عنوان تابع مشتق پذیری از 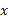تعریف می کند. حال می توانیم به دلیل این مطلب پی ببریم:f معکوس دارد زیرا مشتقش هرگز صفر نمی شود، وf-1 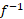بنا به قاعده 11 مشتق پذیر است. این معکوس را 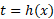نامیدیم.

مثال4اگر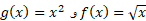، آنگاه 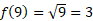نشان دهید همان گونه که رابطه(4) پیش بینی می کند،.

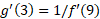حل: داریم

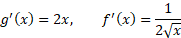
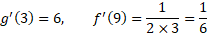
بنابراین

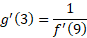
مثال5 درستی رابطه (4) را به کمک تابع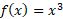 و معکوسش 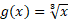، در نقطه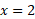، بیازمایید. به عبارت دیگر نشان دهید  که

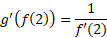
حل: داریم

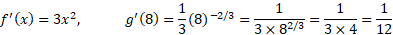
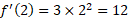
پس،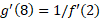

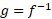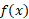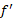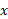حسن رابطه (4) در این است که دقیقا به ما می گوید چگونه مشتق در  ) را محاسبه کنیم: عکس مقدار در  را محاسبه می کنیم. این قاعده مانند قاعده زنجیری فرمول بندی کوتاهتری هم دارد که به خاطر سپردن آن ساده تر، اما حاوی اطلاع کمتری است: اگر 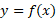، و معکوسش 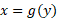مشتق پذیر باشند، آنگاه

راه های دیگر تعبیر قاعده 11

رابطه (4) را به صورت

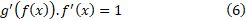
هم می توان نوشت که یاداور قاعده رنجیری است. در واقع، ارتباطی بین این دو وجود دارد. اگر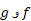 توابع مشتق پذیری باشند که معکوس یکدیگر هم هستند، آنگاه

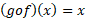
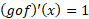
 و بنا قاعده زنجیری داریم

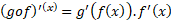
یا

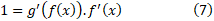
اگر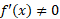، آنگاه از رابطه (7) می توان 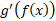را به دست آورد

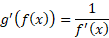
و این همان رابطه (4) است. ( با وجود این، با استنتاج رابطه(4) از قاعده زنجیری، قاعده 11 ثابت نمی شود زیرا در این استنتاج از مشتق پذیر بودن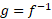 استفاده می شود.)  راه دیگر تعبیر قاعده 11 این است که: اگر در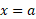 مشتق پذیر باشد، آنگاه 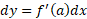این بدین معناست که 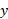، تقریبا 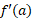بار تندتر از 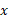تغییر می کند، و تغییر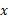، تقریبا  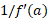بار از تغییر 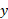تندتر است.

تابع های مثلثاتی معکوس

منشا توابع مسائلی است که در ان ها باید با استفاده از اندازه اضلاع یک مثلث، زوایای آن را به دست آوریم. این توابع پادمشتق بسیاری ازتوابع هم هستند و لذا در جواب های تعدادی از معادلات دیفرانسیل مورد بحث در ریاضیات، مهندسی و فیزیک ظاهر می شوند.

آرک سینوس

تابع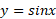  یک به یک نیست؛ این تابع بر هر بازه به طول 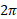دوبار سراسر برد مقادیرش، از 1- تا 1، را طی می کند. ولی اگر دامنه سینوس را به بازه از 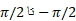محدود کنیم، می بینیم که تابع محدود شده

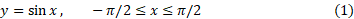
یک به یک است. لذا معکوسی دارد مطابق شکل زیر که با

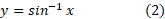
نمایش داده می شود. این تساوی چنین خوانده می شود «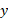 برابر است با آرک سینوس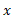» و غالبا به صورت

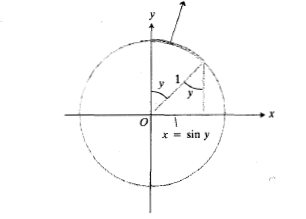
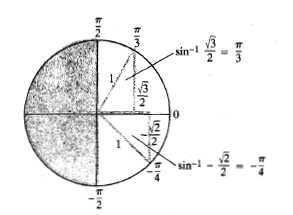
نوشته می شود. شکل زیر تعبیر هندسی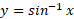 که در آن 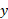مثبت است به دست می دهد. اگر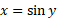، آنگاه 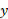آرکی از دایره واحد است که سینوس 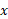می باشد.

به ازای هر مقدار در بازه ، 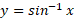عددی است از بازه 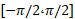که سینوس آن 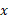است. مثلا شکل زیر

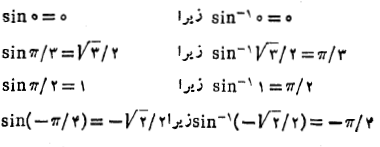
نمودار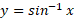 در شکل زیر نمایش داده شده است. خم آبی رنگ در شکل، قرینه نمودار 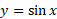نسبت به خط 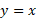است؛ لذا نمودار 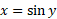می باشد. نمودار  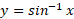بخشی است از این خم که بین است.

عدد 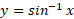 نما نیست؛ معنای آن «معکوس»است، نه «عکس». عکس 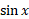عبارت است از

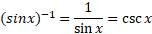
نمودار ارک سینوس در شکل بالا نسبت به مبدا متقارن است زیرا نمودار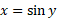 نسبت به مبدا متقارن است. از نظر جبری، این بدین معناست که به ازای هر 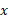در دامنه آرک سینوس،

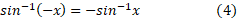
که را ه دیگری است برای بیان این مطلب که تابع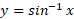 فرد است.

آرک کسینوس

تابع کسینوسی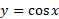 هم نظیر تابع سینوسی یک به یک نیست، اما اگر به بازه 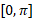محدود شود

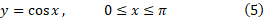
یک به یک است. بنابراین این تابع محدود شده معکوس دارد،

و به آرک کسینوس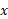 معروف است. به ازای هر مقدار 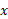دربازه 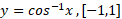عددی است از بازه  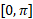که کسینوس آن 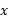است. نمودار 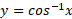را در شکل زیر می بینید.

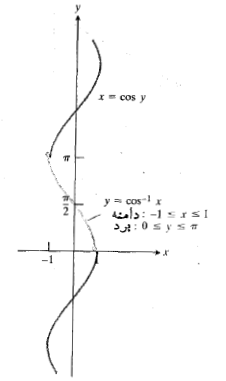
همانگونه که در شکل زیر دیده می شود، آرک کسینوس در اتحاد

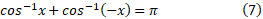
یا

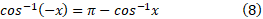
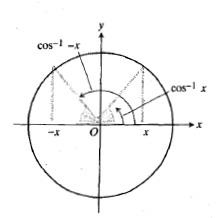
صدق می کند.با توجه به مثلث شکل زیر دیده می شود که به ازای ،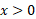

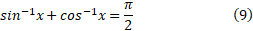
زیرا در این صورت 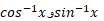 زوایای متمم در یک مثلث قائم الزاویه اند که طول وترش یک واحد و طول یکی از ساق هایش 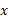واحد است. معادله (9) به ازای سایر مقادیر 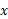واقع در 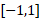هم بر قرار است، اما از شکل مثلث این مطلب نتیجه نمی شود. با این حال، این نتیجه ای است از روابط (4) و (8) .

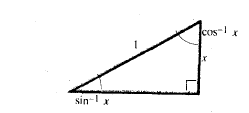
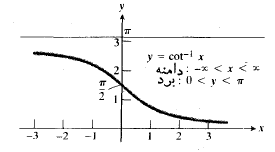
معکوس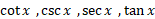

چهار تابع مثلثاتی اساسی دیگر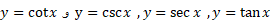 هم ، وقتی به طور مناسبی محدود شوند، معکوس دارند. معکوس

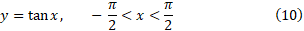
یا

نمایش داده می شود. دامنه آرک تانژانت تمام اعداد حقیقی است، و بردش، بازه باز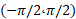 است. به ازای هر مقدار 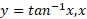 زاویه ای است بین و تانژانت آناست. نمودار در شکل زیر نشان داده شده است.

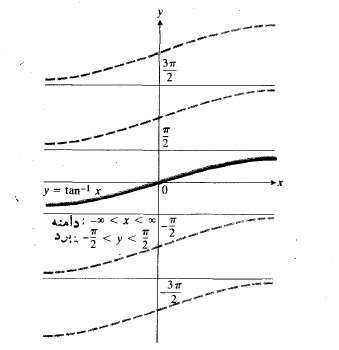
نمودار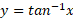 نسبت به مبدا متقارن است زیرا شاخه ای است از نمودار 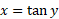مه نسبت به مبدا متقارن است. از نظری جبری، این بدین معناست که

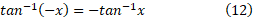
آرک تانژانت هم نظیر آرک سینوس تابع فردی از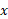 است. نمودار معکوس های توابع (محدود شده)

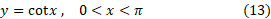
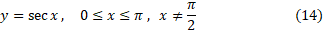
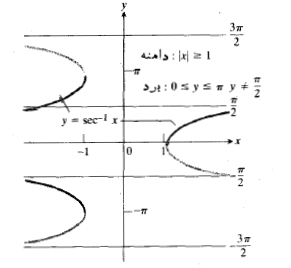
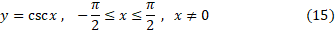
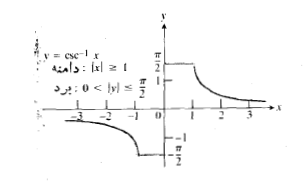
این توابع چنان انتخاب شده اند که در روابط زیر صدق کنند.

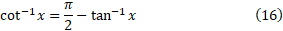
تعبیر به کمک مثلث قائم الزاویه

تعبیر توابع معکوس به کمک مثلث قائم الزاویه، مطابق شکل. در مسائل انتگرال گرایی که به جا نشانی نیاز دارند می تواند مفید باشد.

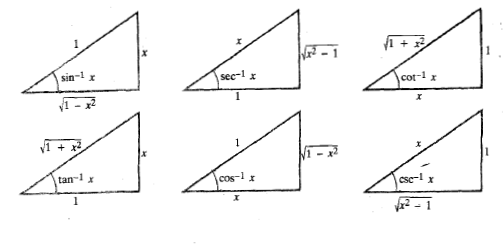
مثال1 با فرض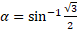 مطلوب است.

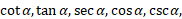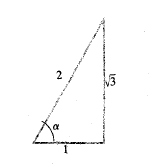
حل: یک مثلث مرجع نظیر مثلث بالا رسم می کنیم؛ طول وتر را 2 و طول ضلع قائم را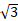 می گیریم. سپس طول ضلع دیگر را محاسبه می کنیم: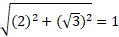. بدین ترتیب مقادیر توابع مثلثاتی 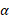به صورت نسبت طول اضلاع به دست می آیند

دامنه و برد برای مراجعه سریع

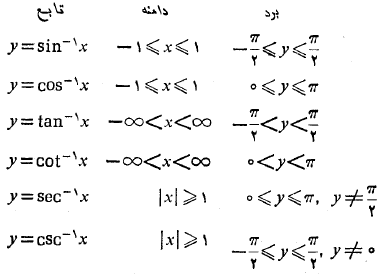
مثال 2 اصلاح مسیر. خلبان هواپیمایی که از شیکاگو به سنت لوئیس می رود متوجه می شود که 12 مایل دور از مسیر اصلی است همانند شکل . مطلوب است زاویه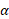 بین این مسیر و مسیر موازی با مسیر اصلی، زاویه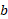، و زاویه اصلاح.

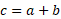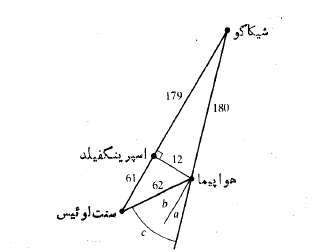
حل:

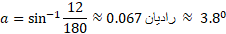
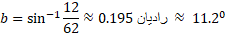
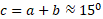
برای مطالعه مباحث بیشتر در این زمینه از محصولکپسول آموزش ریاضیات عمومی 1 در سایتلینوماستفاده کنید.