مقدار میانگین یک تابع
همه ما با روش یافتنمقدار میانگین تعداد متناهی از داده ها آشناییم. مثلا اگر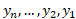
نمرات
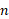شاگرد یک کلاس باشد، میانگین نمرات کلاس برابر است با
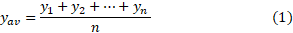
وقتی تعداد داده ها نامتناهی باشد، مثلا وقتی که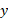
تابعی پیوسته چون
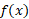روی بازه ای چون
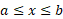باشد، رابطه (1) را نمی توان به کاربرد، زیرا این معادله به صورت مبهم
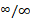در می آید. در چنین حالتی مقدار میانگین
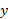نسبت به 
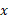را باانتگرال زیر تعریف می کنیم.
تعریف مقدار میانگین یک تابع
مقدار میانگین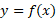
نسبت به
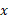برابر است با
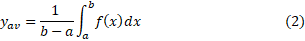
تساوی (2) یک تعریف است و بنابراین نیازی به اثبات ندارد. راه رسیدن به این فرمول چنین است: از کل «جامعه» مقادیر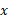
،
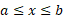، «نمونه» ای چون 
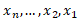که توزیعی یکنواخت دارد و
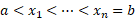، بر می گزینیم. سپس به کمک رابطه(1) میانگین مقادیر تابع
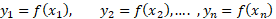
متناظر با این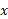
های نمونه را محاسبه می کنیم. داریم
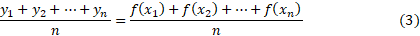
چون باید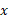
ها یکنواخت باشند، فاصله بین آن ها را با
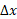می گیریم. پس
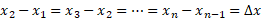
و
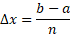
حال در رابطه(3) در مخرج به جای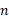
، کسر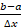
را قرار می دهیم
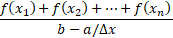
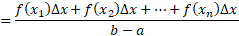
اکنون اگر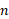
بزرگ و
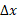کوچک باشد، عبارت
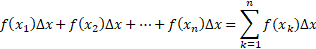
تقریبا برابر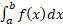
می شود. در واقع حد این عبارت وقتی که
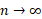دقیقا برابر است با
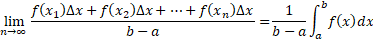
این عبارت همان عبارتی است که بنا به تساوی(2) تعریف مقدار میانگین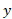
است .
مثال 1 مقدار میانگین تابع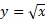
نسبت به
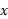از
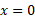تا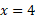
چنین است
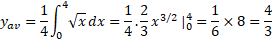
مثال2 ( این مثال یک تعبیر هندسی از رابطه (2) به ازای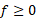
است.)
اگر طرفین رابطه(2) را در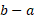
ضرب کنیم داریم
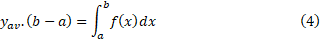
از طرف راست رابطه(4) مساحت بین خم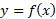
و محور 
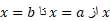است. طرف چپ این تساوی را می توان به عنوان مساحت مستطیلی به ارتفاع
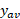و قاعده
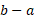تعبیر کرد. بنابراین رابطه(4) تعبیر هندسی از
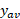به عنوان ارتفاع خم
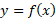به دست می دهد که می تواند در ساختن مستطیلی به کار رود که قاعده اش بازه
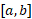و مساحتش برابرمساحت زیر خم باشد. شکل زیر
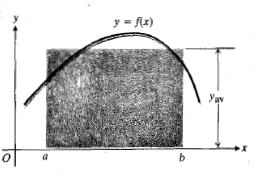
از مقادیر میانگین در محاسبه ولتاز و جریان موثر در مدارهای الکتریکی استفاده می کنیم.
مثال3 مسافتی که جسم متحرکی با سرعت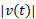
روی خط راستی از لحظه
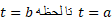می پیماید چنین است
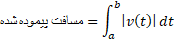
بنابراین، سرعت میانگین(متوسط) این حرکت چنین است
از این رو سرعت متوسط برابر مقدار میانگین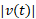
روی
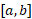است.
میانگین موجودی روزانه
از مفهوم مقدار میانگین در نظریه های اقتصادی برای بررسی میانگین موجودی روزانه استفاده می شود. اگر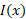
تعداد رادیوها یا کفش ها یا هر کالای دیگری باشد که کارخانه ای در روز 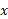در اختیار دارد، آنگاه
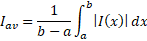
را میانگین موجودی روزانه آن کالا در مدت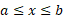 می نامند. هزینه های محل انبار کردن، آب و برق و گازو تلفن، بیمه، و نگهداری، بخش عمده ای از هزینه های انبار داری است، و موجودی روزانه کارخانه می تواند نقش مهمی در تعیین این هزینه ها داشته باشد.
مثال4 میانگین موجودی روزانه چنین است
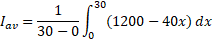
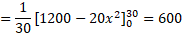
میانگین هزینه روزانه نگهداری شکلات ها برابر است با حاصل ضرب هزینه نگهداری یک صندوق شکلات در میانگین موجودی روزانه. پس
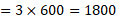میانگین هزینه روزانه نگهداری شکلات ها
یعنی برابر 1800ریال در روز.
گشتاور و مرکز جرم
در تحلیل سازه ها و سیستم های مکانیکی در مهندسی و فیزیک، غالبا جرم آن ها را چنان در نظر می گیرند که گویی در یک نقطه متمرکزند. این نقطه را مرکز جرم می نامند. اچاری که در حال سقوط است ممکن است حول مرکز جرمش دوران کند، اما حود مرکز جرم در امتداد یک خط راست سقوط می کند مانند شکل.
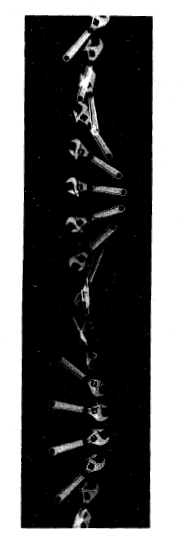
باید روش تعیین مرکز جرم را که اساسا یک مسالهریاضی است بدانیم. در این مقاله چگونگی جل این مساله را نشان می دهیم و مرکز جرم تعدادی از شکل های متداول را به دست می آوریم ولی در اینجا تنها به اشکال یک یا دو بُعدی می پردازیم.
جرم های روی یک خط
اگر مطابق شکل زیر جرم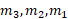
روی محور
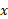باشند و نقطه اتکای محور در مبدا باشد، این سیستم ممکن است در حالت تعادل باشد و یا نباشد. هرکدام از این جرم ها نیرویی برابر
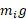(حاصل ضرب جرم در شتاب گرانش) به طرف پایین وارد می آورد و هریک از این نیروها تمایل دارد محور را حول مبدا بچرخاند. این کیفیت را گشتاور نیرو می نامند که بنا به تعریف برابر است با حاصل ضرب نیروی 
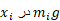یعنی در فاصله علامت دار جرم تا مبدا.
فاصله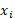 
در مورد جرم های سمت چپ مبدا منفی و در مورد جرم های سمت راست مبدا مثبت است. بنابراین جرم های سمت چپ و راست مبدا گشتاورهای مخالف ایجاد می کنند. کل گشتاور نیرو، با تمایل سیستم به گردش حول مبدا برابر است با مجموع 
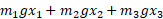. اگر این مجموع برابر صفر باشد سیستم متعادل و درغیراین صورت نامتعادل است.
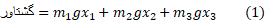
اگر از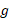
فاکتور بگیریم، گشتاور نیرو چنین می شود
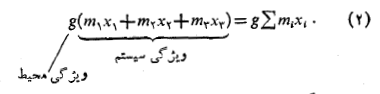
بنابراین، گشتاور برابر است با حاصل ضرب شتاب گرانش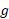
( ویژگی محیطی که سیستم در آن قرار دارد) در مقدار 
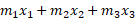(ویژگی خود سیستم که ثابت است و به محیط بستگی ندارد.) مقدار
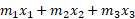که از این پس به صورت
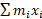نوشته می شود گشتاور سیستم حول مبدا نام دارد
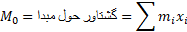
در هرجایی که سیستم قرار داشته باشد، در ماه، مریخ، یا در زمین، گشتاور یکسان است. در چه نقطه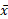
ی از محور، کل جرم،
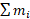، را قرار دهیم تا همان گشتاور نیرو را ایجاد کند؟ برای یافتن این محل دو گشتاور را مساوی قرار می دهیم و معادله حاصل را نسبت به
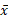حل می کنیم.
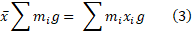
یا
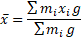
از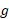
فاکتور می گیریم وآن را از صورت و مخرج حذف می کنیم
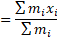
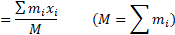
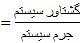
به دو نکته باید توجه کرد: نخست، برای محاسبه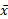
گشتاور سیستم حول مبدا را بر جرم سیستم تقسیم می کنیم. دوم، نبودن
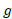حاکی است که
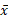یک ویژگی ذاتی سیستم است و به محیط بستگی ندارد. اهمیت
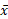در این است که این کمیت مرکز جرم سیستم است. سیستم وقتی متعادل می شود که نقطه اتکا در
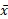قرار گیرد.
گشتاور هر کدام ازجرم ها حول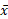
برابر است با
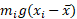یعنی برابر است با حاصل ضرب وزن
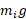در فاصله علامت دار جرم 
. بنا به محاسبات زیر مجموع این گشتاورها صفر است
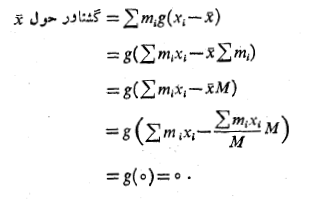
سیم ها و میله های باریک
در بسیاری از کاربردها، می خواهیم مرکز جرم یک سیم یا میله راست، یا نوار فلزی باریک را پیدا کنیم. در چنین مواردی که می توان فرض کرد توزیع جرم پیوسته است، چنانکه خواهیم دید علائم جمع در فرمول های مرکز جرم به علائمانتگرال تبدیل می شود.
نوار باریک و بلندی را در نظر بگیرید که مطابق شکل به قطعات کوچکی با جرم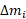
تقسیم شده است.
هر قطعه طولی برابر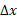
واحد دارد و فاصله اش از مبدا تقریبا به اندازه
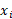واحد است. اولا مرکز جرم نوار،
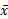، حدودا همان مرکز جرم سیستم جرم های
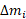است.
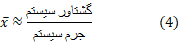
ثانیا، گشتاور هر قطعه از نوار حول مبدا تقریبا برابر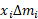
است. بنابراین گشتاور کل سیستم جرم ها حول مبدا تقریبا برابر مجموع
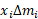ها است.
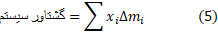
ثالثا، اگرچگالی نوار در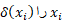 
( برحسب جرم در واحد طول) بگیریم، آنگاه 
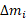تقریبا برابر
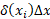( جرم در واحد طول ضربدر طول) می شود
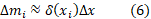
از ترکیب این سه رابطه داریم
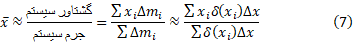
مجموع های کسر آخر رابطه (7) مجموع هایتقریب زننده انتگرال اند. وقتی تقسیم بندی نوار ظریف تر شود و طول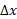
به صفر میل کند، تقریبا بهتر می شوند و به رابطه زیر می انجامند.
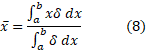
از این فرمول برای محاسبه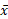
استفاده می کنیم.
گشتاور، جرم، و مرکز جرم یک میله، سیم،یا نوار باریک واقع در امتداد محور
اگر چگالی جسم ثابت نباشد و نسبت به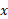
تغییر کند، آنگاه در روابط (9) مقدار
تابعی از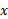
است که باید در محاسبه انتگرال هاآن را منظور کرد. اما چنانچه چگالی
ثابت باشد مثلا در مورد نواری که عرض و ضخامت یکنواختی دارد و جنس سراسر آن یکی است، آنگاه، ثابت
را می توان از انتگرال ها خارج کرد و در محاسبه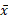
آن را حذف کرد.
مثال1 نوار باریکی با چگالی یکنواخت (یعنی ثابت) در امتداد محور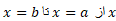
قرار می گیرد مطابق شکل.نشان دهید مرکز جرم این نوار در وسط آن است.
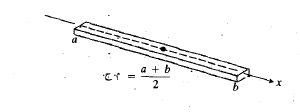
حل: چون چگالی
ثابت است، روابط (9) به صورت زیردر می آید
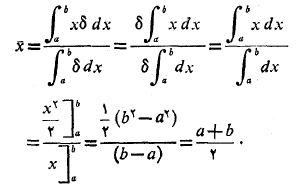
بنابراین مرکز جرم یک نوار (یا میله یا سیم) یکنواخت در وسط آن است.
مثال2 میله ای فلزی که یک سرش در مبدا و سر دیگرش در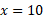
است از چپ به راست ضخیم می شود به طوری که چگالی، یعنی جرم در هر واحد طول آن، ثابت نیست بلکه برابر است با
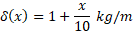
مرکز جرم میله را بیابید.
حل: گشتاورمیله حول مبدا چنین است
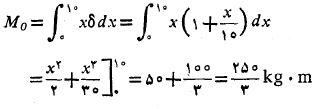
جرم میله برابر است با
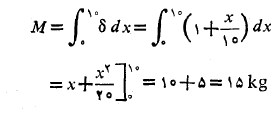
مرکز جرم میله در نقطه زیر قرار دارد
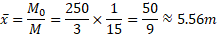
جرم های گسترده در یک صفحه
فرض کنید تعدادی متناهی جرم در اختیار داریم که در صفحه مختصات قرار دارند. جرم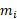
در نقطه
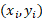قرار دارد مطابق شکل. کل جسم سیستم برابر است با
جرم سیستم: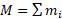
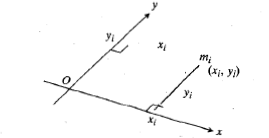
هر کدام از جرم های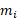
حول هر دو محور گشتاوری ایجاد می کند. گشتاور
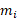حول محور
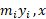؛ و حول محور
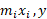است.
گشتاور حول محور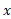
:
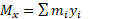
گشتاور حول محور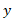
: 
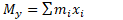
مختص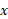
مرکز جرم سیستم بنا به تعریف چنین است
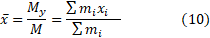
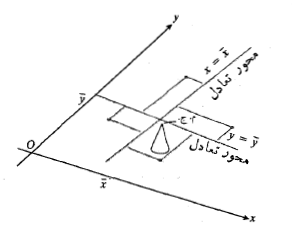
در حالت یک بُعدی اگر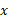
را برابر
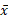برگزینیم سیستم حول خط
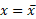به حالت تعادل در می آید مطابق شکل.
مختص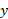
مرکز جرم سیستم بنا به تعریف چنین است
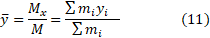
اگر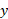
را برابر
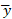بر می گزینیم، سیستم حول خط
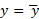نیز به حالت تعادل در می آید. گشتاورهای نیرویی که اجرام حول خط
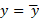وارد می آورند یکدیگر را خنثی می کنند. بنابراین از جهت مساله تعادل، رفتار سیستم مانند وقتی است که همه جرمش در نقطه ای چون
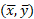، به نام مرکز جرم سیستم، متمرکز باشد.
ورقه های نازک
در بسیاری از کاربردها، بایدمرکز جرم یک ورقه تخت نازک نظیر یک قرص آلومینیومی یا یک ورقه فولادی مثلثی شکل را بیابیم. در این موارد، فرض می کنیم توزیع جرم پیوسته باشد، و فرمول هایی که برای محاسبه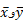
به کار می روند به صورتانتگرالیباشند و نه مجموع های متناهی. این انتگرال ها از راه زیر به دست می آیند.
فرض کنید ورقه ای که در صفحه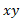 
قرار دارد به نوارهای نازک و موازی با یکی از محورها (مطابق شکل موازی محور
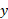) تقسیم می شود.
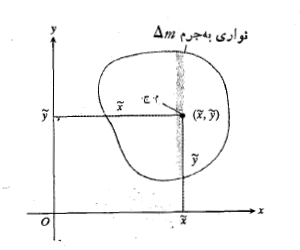
مرکز جرم یک نوار نمونه،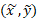
است.(علامت
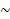روی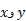
تیلدا نام دارد و لذا 
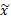را «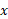
تیلدا» می خوانند.) فرض می کنیم جرم نوار،
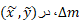متمرکز است. بنابراین گشتاور نوار حول محور
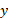برابر است با
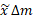، و گشتاور آن حول محور
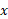برابر است با
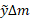. از این رو روابط (10) و (11) به صورت زیر در می آیند
مانند حالت تک بُعدی، مجموع های واقع در صورت و مخرج این رابطه ها مجموع هایتقریب زننده انتگرال هایند و وقتی پهنای نوارها نازک و نازکتر شود به این انتگرال ها میل می کنند. این انتگرال ها را به صورت نمادین چنین می نویسیم
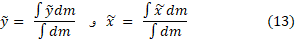
در مثال های زیر روش محاسبه این انتگرال ها آمده است.
گشتاورها، جرم، و مرکز جرم یک ورقه نازک واقع در صفحه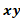 
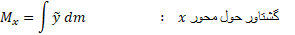
برای نحاسبه این انتگرال ها، شکل ورقه را در صفحه مختصات رسم می کنیم و نواری از جرم را که موازی یکی از محورهای مختصات باشد مشخص می کنیم. سپس جرم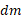
نوار،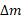
، و مختصات مرکز جرم نوار 
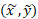را بر حسب
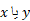بیان می کنیم. سرانجام از
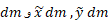بین حدودی که به محل ورقه در صفحه بستگی داردانتگرال می گیریم.
مثال3 ورقه مثلثی شکلی که در شکل زیردیده می شود به خطوط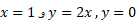
محدود است. چگالی این ورقه یکنواخت و برابر است با
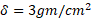. مطلوب است( الف) گشتاور
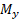ورقه حول محور
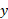، (ب) جرم ورقه،
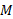، و(پ) مختص
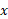مرکز جرم ورقه.
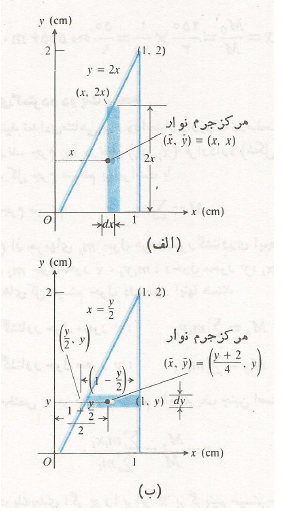
حل: روش1: نوارهای قائم( قسمت الف شکل) ، الف)گشتاور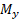
: نوار قائم نمونه ویژگی های زیر را دارد
مرکز جرم: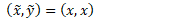 
طول: 
عرض: 
مساحت: 
جرم: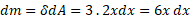 
فاصله مرکز جرم از محور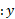
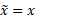
گشتاورنوار حول محور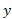
برابر است با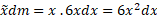 
بنابراین، گشتاورورقه حول محور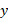
چنین است
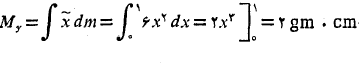
ب)جرم ورقه:
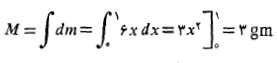
پ) مختص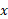
مرکز جرم ورقه:
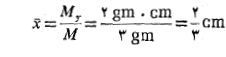
با انجام محاسبات مشابهی می توان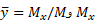 
را نیز یافت.
روش 2: نوارهای افقی( قسمت ب شکل)
الف) گشتاور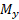
: نوار افقی نمونه مشخصات زیر را دارد
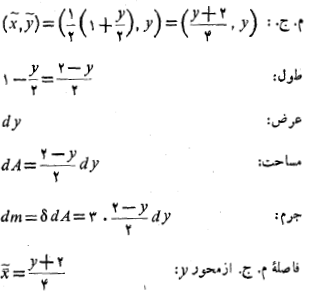
گشتاور نوار حول محور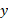
برابر است با
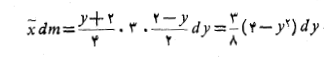
گشتاور ورقه حول محور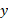 چنین است
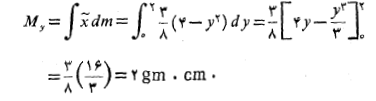
ب) جرم ورقه:
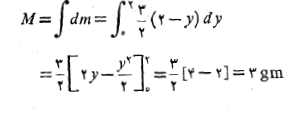
پ) مختص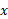
مرکز جرم ورقه:
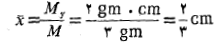
با انجام محاسبات مشابه می توان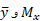
را یافت.
گرانیگاه (مرکز ثقل)، مرکز وار، همگنی، و یکنواختی
وقتی فیزیکدانان از آثار گرانش بر یک سیستم اجرام بحث می کنند ممکن است به جای اصطلاح مرکز از اصطلاح گرانیگاه (مرکزثقل) نا برند. ماده ای که چگالی آن،
، ثابت است ماده همگن، یکنواخت، یا با چگالی یکنواخت نیز نامیده می شود. هرگاه تابع چگالی ثابت باشد، از صورت و مخرج فرمول های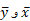
حذف می شود.
وقتی چگالی ثابت است از نظر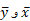مثل آن است که برابر 1 باشد. بنابراین در این حالت مرکز جرم یکی از ویژگی های هندسی جسم است و له جنس ماده ای که از جسم آن ساخته شده است بستگی ندارد. در این مورد بهتر است مرکز جرم را مرکزوار شکل بنامیم و مثلا بگوییم « مرکزوار یک مثلث یا یک مخروط صلب را بیابید». در چنین مواردی را برابر 1 می گیریم و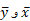 را مانند آنچه گذشت، از تقسیم گشتاورها بر جرم ها به دست می آوریم.
برای مطالعه مباحث بیشتر در این زمینه از محصولکپسول آموزشی ریاضی عمومی 1 در سایت لینوماستفاده کنید.