غلت گشتاوری و تکانه زاویه ای
اجسام غلتان
برای برخی به شعاع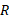 که بطور هموار (بدون لغزیدن) می غلتد داریم
که بطور هموار (بدون لغزیدن) می غلتد داریم
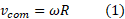
که در آن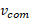 تندی خطیمرکز جرم چرخ و
تندی خطیمرکز جرم چرخ و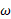 تندی زاویه ای چرخ به دور مرکز آن است. هم چنین می توان تصور کرد که چرخ به طور لحظه ای به دور نقطه
تندی زاویه ای چرخ به دور مرکز آن است. هم چنین می توان تصور کرد که چرخ به طور لحظه ای به دور نقطه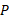 واقع در سطح «جاده» که محل تماس چرخ با جاده است می چرخد. تندی زاویه ای چرخ به دور این نقطه برابر با تندی زاویه ای چرخ به دور مرکز آن است. انرژی جنبشی چرخ غلتان برابر است با
واقع در سطح «جاده» که محل تماس چرخ با جاده است می چرخد. تندی زاویه ای چرخ به دور این نقطه برابر با تندی زاویه ای چرخ به دور مرکز آن است. انرژی جنبشی چرخ غلتان برابر است با
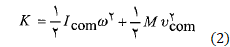
که در آن گشتاور لختی چرخ نسبت به مرکز آن و
گشتاور لختی چرخ نسبت به مرکز آن و 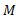 جرم چرخ است. اگر چرخ شتاب پیدا کند، اما باز هم به طور هموار بغلتد، رابطه شتاب مرکز جرم آن
جرم چرخ است. اگر چرخ شتاب پیدا کند، اما باز هم به طور هموار بغلتد، رابطه شتاب مرکز جرم آن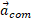 با شتاب زاویه ای نسبت به مرکز
با شتاب زاویه ای نسبت به مرکز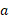 به صورت زیر است
به صورت زیر است
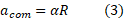
اگر چرخ به طور هموار از یک شیب راهه با زاویه شیب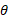 به پایین بغلتد شتاب آن در راستای محور
به پایین بغلتد شتاب آن در راستای محور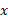 واقع در روی شیب راهه برابر است با
واقع در روی شیب راهه برابر است با

 مسئله نمونه- غلتیدن گلوله به چایین یک شیب راهه
مسئله نمونه- غلتیدن گلوله به چایین یک شیب راهه
گلوله یکنواختی به جرم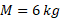 و شعاع
و شعاع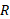 از حال سکون از یک شیب راهه با زاویه شیب
از حال سکون از یک شیب راهه با زاویه شیب 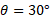 به طور هموار به پایین می غلتد. الف) این گلوله را در راستای قائم به اندازهh=1.2 m
به طور هموار به پایین می غلتد. الف) این گلوله را در راستای قائم به اندازهh=1.2 m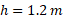 پایین می آید تا به شیب راهه می رسد. تندی گلوله در پایین شیب چقدر است؟
پایین می آید تا به شیب راهه می رسد. تندی گلوله در پایین شیب چقدر است؟
در هنگام غلتیدن گلوله از شیب راهه به پایین، انرژی مکانیکی دستگاه گلوله- زمین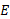 ، پایسته می ماند زیرا تنها نیرویی که روی گلوله کار انجام می دهد نیروی پایستار گرانشی است. نیروی عمودی وارد شده به گلوله از سوی شیب راهه کاری انجام نمی دهد چون بر مسیر حرکت گلوله عمود است. نیروی اصطکاک وارد شده به گلوله از سوی شیب راهه هم هیچ انرژی ای را به انرژی گرمایی تبدیل نمی کند زیرا گلوله نمی لغزد ( گلوله به طور هموار می غلتد).
، پایسته می ماند زیرا تنها نیرویی که روی گلوله کار انجام می دهد نیروی پایستار گرانشی است. نیروی عمودی وارد شده به گلوله از سوی شیب راهه کاری انجام نمی دهد چون بر مسیر حرکت گلوله عمود است. نیروی اصطکاک وارد شده به گلوله از سوی شیب راهه هم هیچ انرژی ای را به انرژی گرمایی تبدیل نمی کند زیرا گلوله نمی لغزد ( گلوله به طور هموار می غلتد).
بنابراین، قانون پایستگی انرژی مکانیکی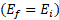 را می توان به صورت زیر نوشت
را می توان به صورت زیر نوشت
(1-1)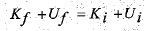
در این معادله شاخص های پایین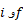 ، به ترتیب معرف مقادیر پایانی ( در پایین شیب راهه ) و مقادیر آغازی ( در حالت سکون ) هستند. انرژی پتانسیل گرانشی در آغاز
، به ترتیب معرف مقادیر پایانی ( در پایین شیب راهه ) و مقادیر آغازی ( در حالت سکون ) هستند. انرژی پتانسیل گرانشی در آغاز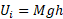 (
(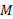 جرم گلوله است) و در پایان
جرم گلوله است) و در پایان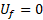 است. انرژی جنبشی در آغاز
است. انرژی جنبشی در آغاز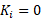 است. در مورد انرژی جنبشی پایانی
است. در مورد انرژی جنبشی پایانی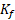 ، به نکته کلیدی دیگری نیاز داریم. چون گلوله می غلتد انرژی جنبشی شامل انرژی های جنبشی انتقالی و دورانی است.
، به نکته کلیدی دیگری نیاز داریم. چون گلوله می غلتد انرژی جنبشی شامل انرژی های جنبشی انتقالی و دورانی است.
محاسبات: با جانشانی همه رابطه ها در معادله (1-1) داریم
(1-2)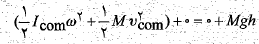
که در آن لختی دورانی گلوله نسبت به محور گذرنده از مرکز جرم،
لختی دورانی گلوله نسبت به محور گذرنده از مرکز جرم،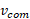 تندی خواسته شده و
تندی خواسته شده و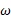 تندی زاویه ای در پایین شیب راهه است. چون گلوله به طور هموار می غلتد، با استفاده کردن از معادله
تندی زاویه ای در پایین شیب راهه است. چون گلوله به طور هموار می غلتد، با استفاده کردن از معادله 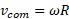 مقدار
مقدار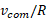 را به جای
را به جای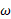 قرار می دهیم تا از عده مجهول ها در معادله (1-2) کاسته شود. با انجام دادن این کار و قرار دادن
قرار می دهیم تا از عده مجهول ها در معادله (1-2) کاسته شود. با انجام دادن این کار و قرار دادن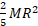 به جای
به جای و حل کردن معادله حاصل نسبت به
و حل کردن معادله حاصل نسبت به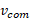 داریم
داریم
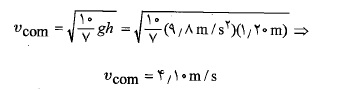
توجه کنید که این پاسخ به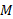 یا
یا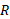 بستگی ندارد.
بستگی ندارد.
ب) هنگامی که گلوله به پایین شیب راهه می غلتد بزرگی و جهت نیروی اصطکاک وارد شده به آن چیست؟
محاسبات: در ابتدا شتاب گلوله را به دست می آوریم:
را به دست می آوریم:
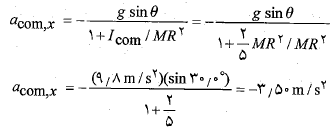
توجه کنید که برای پیدا کردن ، هیچ نیازی به جرم
، هیچ نیازی به جرم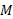 یا شعاع
یا شعاع 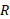 نبود. بنابراین گلوله با هر اندازه و با هر جرم (یکنواخت) هنگام پایین رفتن از شیب راهه 30 درجه دارای همین شتاب خواهد بود.
نبود. بنابراین گلوله با هر اندازه و با هر جرم (یکنواخت) هنگام پایین رفتن از شیب راهه 30 درجه دارای همین شتاب خواهد بود.
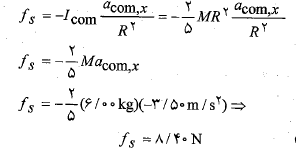
بنابراین نیروی اصطکاک وارد شده به هر گلوله ای به جرم 6 کیلوگرم که از یک شیب راهه 30 درجه به طور هموار به پایین می غلتد بدون توجه به شعاع گلوله برابر با 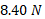 است اما این نیرو برای جرم بزرگ تر بیشتر خواهد بود.
است اما این نیرو برای جرم بزرگ تر بیشتر خواهد بود.
خاصیت برداری گشتاور نیرو
در دستگاه مختصات سه بُعدی گشتاور نیروی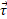 کمیتی برداری است که نسبت به یک نقطه ثابت ( به طور معمول مبداء مختصات) تعریف می شود؛ این بردار برابر است با
کمیتی برداری است که نسبت به یک نقطه ثابت ( به طور معمول مبداء مختصات) تعریف می شود؛ این بردار برابر است با
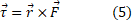
که در آن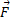 نیروی وارد شده به یک ذره و
نیروی وارد شده به یک ذره و بردار مکان معین کننده محل ذره نسبت به نقطه ثابت ( یا مبداء مختصات) است. بزرگی
بردار مکان معین کننده محل ذره نسبت به نقطه ثابت ( یا مبداء مختصات) است. بزرگی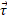 چنین به دست می آید
چنین به دست می آید
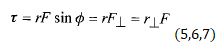
که در آن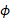 زاویه میان
زاویه میان 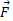 و
و ،
،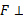 مولفه
مولفه 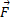 در راستای عمود بر
در راستای عمود بر و
و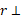 بازوی گشتاور
بازوی گشتاور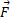 است. جهت
است. جهت از قاعده دست راست مربوط به حاصل ضرب برداری معین می شود.
از قاعده دست راست مربوط به حاصل ضرب برداری معین می شود.
 مسئله نمونه- گشتاور ناشی از نیروی وارد شده به یک ذره
مسئله نمونه- گشتاور ناشی از نیروی وارد شده به یک ذره
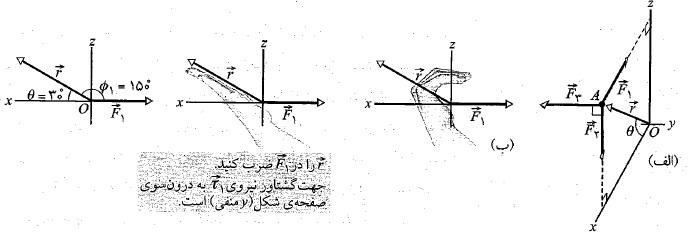
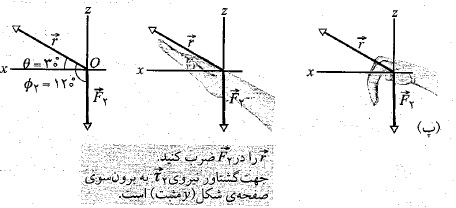
در شکل زیر قسمت الف سه نیرو، هرکدام به بزرگی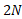 به ذره ای وارد می شوند. ذره در صفحه
به ذره ای وارد می شوند. ذره در صفحه 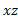 و در نقطه
و در نقطه 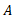 که با بردار مکان
که با بردار مکان مشخص می شود قرار دارد و
مشخص می شود قرار دارد و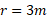 و
و 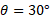 . گشتاور نیروی حاصل از هریک از نیروها نسبت به مبداء
. گشتاور نیروی حاصل از هریک از نیروها نسبت به مبداء 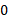 چیست؟
چیست؟
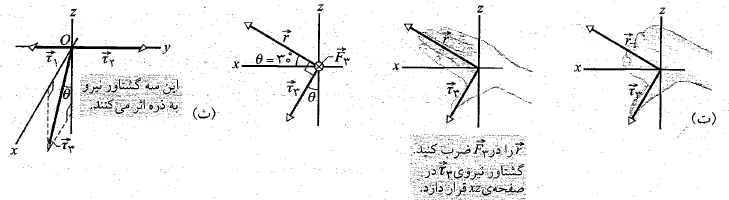
چون سه بردار نیرو در یک صفحه قرار ندارند باید از ضرب برداری استفاده کنیم. بزرگی بردارها از معادله(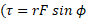 و جهت آن ها از قاعده دست راست به دست می آید.
و جهت آن ها از قاعده دست راست به دست می آید.
محاسبات: چون می خواهیم گشتاور های نیرو را نسبت به مبداء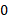 به دست آوریم، بردار
به دست آوریم، بردار مورد نیاز برای هر ضرب برداری همان بردار مکان داده شده است. برای تعیین
مورد نیاز برای هر ضرب برداری همان بردار مکان داده شده است. برای تعیین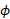 ، زاویه میان
، زاویه میان و هریک از نیروها، بردارهای نیرو در قسمت الف شکل را به نوبت طوری جابه جا می کنیم که دُم آن ها در مبداء قرار گیرد. قسمت های ب، پ و ت شکل که نمایش دهنده مستقیم صفحه
و هریک از نیروها، بردارهای نیرو در قسمت الف شکل را به نوبت طوری جابه جا می کنیم که دُم آن ها در مبداء قرار گیرد. قسمت های ب، پ و ت شکل که نمایش دهنده مستقیم صفحه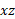 هستند، به ترتیب بردارهای نیروی جابه جا شده
هستند، به ترتیب بردارهای نیروی جابه جا شده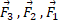 را نشان می دهند. ( توجه کنید که دیدن زاویه های میان بردارهای نیرو و بردار مکان چقدر آسان تر شده است). در قسمت ت شکل، زاویه میان
را نشان می دهند. ( توجه کنید که دیدن زاویه های میان بردارهای نیرو و بردار مکان چقدر آسان تر شده است). در قسمت ت شکل، زاویه میان و
و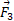 برابر با 90 درجه است و نماد
برابر با 90 درجه است و نماد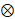 نشان می دهد که جهت
نشان می دهد که جهت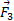 به درون سوی صفحه شکل است. اگر جهت نیرو به برئن سوی صفحه شکل می بود با نماد
به درون سوی صفحه شکل است. اگر جهت نیرو به برئن سوی صفحه شکل می بود با نماد نشان داده می شد. اکنون بزرگی گشتاورها به صورت زیر به دست می آیند.
نشان داده می شد. اکنون بزرگی گشتاورها به صورت زیر به دست می آیند.
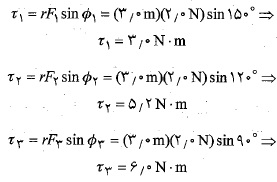
اکنون برای تعیین جهت این گشتاورهای نیرو از قاعده دست راست استفاده می کنیم، یعنی انگشتان دست راست را طوری قرار می دهیم که از به طرف
به طرف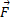 و تحت زاویه کوچک تر میان راستاهای آن ها بپیچند. در این صورت انگشت شست جهت گشتاور نیرو را نشان خواهد داد. بنابراین جهت
و تحت زاویه کوچک تر میان راستاهای آن ها بپیچند. در این صورت انگشت شست جهت گشتاور نیرو را نشان خواهد داد. بنابراین جهت 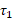 در قسمت ب شکل ، به درون سوی صفحه و جهت
در قسمت ب شکل ، به درون سوی صفحه و جهت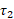 در قسمت پ شکل به برون سوی صفحه شکل است. جهت
در قسمت پ شکل به برون سوی صفحه شکل است. جهت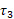 در قسمت ت شکل، به گونه ای است که نشان داده شده است. تمام این بردارهای گشتاور نیرو در قسمت ث شکل نشان داده شده اند.
در قسمت ت شکل، به گونه ای است که نشان داده شده است. تمام این بردارهای گشتاور نیرو در قسمت ث شکل نشان داده شده اند.
تکانه زاویه ای یک ذره
تکانه زاویه ای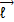 ، ذره ای باتکانه خطی
، ذره ای باتکانه خطی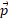 ، جرم
، جرم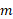 و سرعت خطی
و سرعت خطی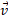 ، کمیتی برداری است که نسبت به یک نقطه ثابت ( به طور معمول مبداء مختصات) تعریف می شود. معادله این بردار چنین نوشته می شود
، کمیتی برداری است که نسبت به یک نقطه ثابت ( به طور معمول مبداء مختصات) تعریف می شود. معادله این بردار چنین نوشته می شود
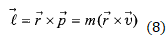
(9)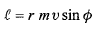
(10)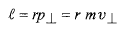
(11)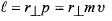
که در آن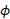 زاویه میان
زاویه میان 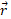 و
و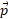 ،
،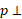 و
و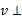 مولفه های
مولفه های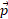 و
و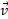 در راستای عمود بر
در راستای عمود بر و
و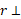 فاصله عمودی نقطه ثابت از امتداد
فاصله عمودی نقطه ثابت از امتداد 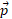 است. جهت
است. جهت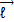 از قاعده دست راست مربوط به حاصل ضرب برداری معین می شود.
از قاعده دست راست مربوط به حاصل ضرب برداری معین می شود.
شکل زاویه ای قانون دوم نیوتون
قانون دوم نیوتون در شکل زاویه ای برای یک ذره چنین نوشته می شود
(12)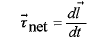
که در آن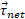 گشتاور نیروی برایند وارد شده به ذره و
گشتاور نیروی برایند وارد شده به ذره و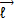 تکانه زاویه ای ذره است.
تکانه زاویه ای ذره است.
 مسئله نمونه- گشتاور نیرو و مشتق تکانه زاویه ای نسبت به زمان
مسئله نمونه- گشتاور نیرو و مشتق تکانه زاویه ای نسبت به زمان
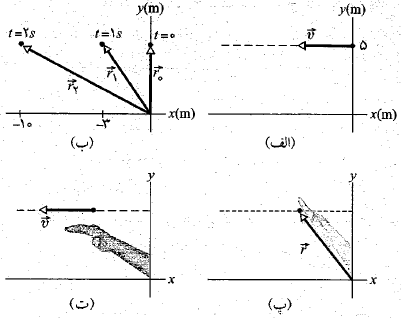
شکل زیرچارچوب ثابت یک ذره 0.5 کیلوگرمی را نشان می دهد که با بردار مکان به معادله زیر در راستای یک خط راست از زمان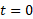 شروع به حرکت می کند.
شروع به حرکت می کند.
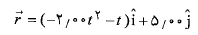
در این معادله برحسب متر و
برحسب متر و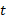 بر حسب ثانیه است. بردار از مبداء مختصات به سمت ذره است. رابطه مربوط به تکانه زاویه ای ذره
بر حسب ثانیه است. بردار از مبداء مختصات به سمت ذره است. رابطه مربوط به تکانه زاویه ای ذره 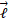 ، گشتاور نیروی وارد شده به ذره
، گشتاور نیروی وارد شده به ذره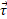 ، هر دو را به مبداء مختصات به صورت نمادگذاری بردارهای یکه به دست آورید. علامت های جبری این کمیت ها را با توجه بهحرکتذره توجیه کنید.
، هر دو را به مبداء مختصات به صورت نمادگذاری بردارهای یکه به دست آورید. علامت های جبری این کمیت ها را با توجه بهحرکتذره توجیه کنید.

محاسبات: هنگام استفاده از معادله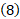 برای پیدا کردن تکانه زاویه ای نسبت به مبداء مختصات نخست باید با مشتق گرفتن از بردار مکان بر حسب زمان برای سرعت ذره رابطه ای به دست آوریم. با استفاده کردن از معادله
برای پیدا کردن تکانه زاویه ای نسبت به مبداء مختصات نخست باید با مشتق گرفتن از بردار مکان بر حسب زمان برای سرعت ذره رابطه ای به دست آوریم. با استفاده کردن از معادله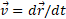 چنین می نویسیم
چنین می نویسیم
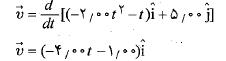
در اینجا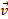 بر حسب متر بر ثانیه است.
بر حسب متر بر ثانیه است.
اکنون حاصلضرب برداری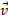 و
و را با استفاده کردن از الگوی مربوط به ضرب های برداری حساب می کنیم
را با استفاده کردن از الگوی مربوط به ضرب های برداری حساب می کنیم
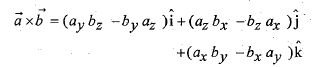
در اینجا نماد کلی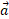 به جای
به جای و نماد کلی
و نماد کلی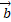 به جای
به جای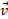 قرار گرفته است. اما چون نمی خواهیم به کاری بیش از آنچه که نیاز داریم بپردازیم نخست فقط درباره جانشانی ها در ضرب برداری فکر می کنیم. چون
قرار گرفته است. اما چون نمی خواهیم به کاری بیش از آنچه که نیاز داریم بپردازیم نخست فقط درباره جانشانی ها در ضرب برداری فکر می کنیم. چون بدون مولفه
بدون مولفه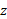 و
و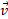 بدون مولفه
بدون مولفه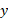 یا
یا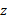 است، تنها جمله ناصفر در ضرب برداری جمله آخر
است، تنها جمله ناصفر در ضرب برداری جمله آخر 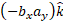 است. بنابراین محاسباتریاضی را چنین دنبال می کنیم.
است. بنابراین محاسباتریاضی را چنین دنبال می کنیم.
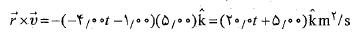
توجه کنید که مانند همیشه نتیجه ضرب برداری یک بردار است که بر بردارهای اولیه عمود است. نتیجه بالا را در جرم ضرب می کنیم و رابطه زیر را به دست می آوریم
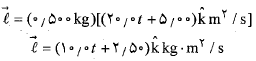
گشتاور نیرو نسبت به مبداء چنین به دست می آید
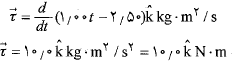
نتیجه به دست آمده برای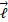 نشان می دهد که تکانه زاویه ای در جهت مثبت محور
نشان می دهد که تکانه زاویه ای در جهت مثبت محور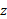 واقع است. برای توجیه کردن این نتیجه مثبت با توجه به دوران بردار مکان ، آن بردار را در چند زمان حساب می کنیم:
واقع است. برای توجیه کردن این نتیجه مثبت با توجه به دوران بردار مکان ، آن بردار را در چند زمان حساب می کنیم:
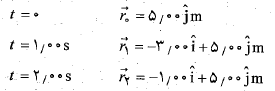
با رسم کردن این نتیجه ها به صورت قسمت ب شکل می بینیم که در جهت پادساعت گرددوران می کند تا با ذره بماند. این جهت ، جهت مثبت دوران است. بنابراین ذره گرچه به خط راست حرکت می کند، هنوز در جهت پاد ساعت گرد به دور مبداء مختصات می چرخد و در نتیجه دارای تکانه زاویه ای مثبت است.
در جهت پادساعت گرددوران می کند تا با ذره بماند. این جهت ، جهت مثبت دوران است. بنابراین ذره گرچه به خط راست حرکت می کند، هنوز در جهت پاد ساعت گرد به دور مبداء مختصات می چرخد و در نتیجه دارای تکانه زاویه ای مثبت است.
جهت 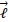 را نیز با استفاده کردن از قاعده دست راست مربوط به ضرب برداری ( در اینجا
را نیز با استفاده کردن از قاعده دست راست مربوط به ضرب برداری ( در اینجا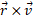 ، یا اگر دوست داشته باشید
، یا اگر دوست داشته باشید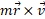 که در همان جهت است) می توان معین کرد. برای هر لحظه ای در حینحرکت کردن ذره، انگشت های دست راست ابتدا در جهت بردار اول
که در همان جهت است) می توان معین کرد. برای هر لحظه ای در حینحرکت کردن ذره، انگشت های دست راست ابتدا در جهت بردار اول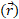 در ضرب برداری قرار می گیرند همانند قسمت پ شکل . بنابراین سمت گیری دست ( روی صفحه کتاب یا صفحه نمایش) به گونه ای تنظیم می شود که انگشت ها بتوانند به راحتی بچرخند و در جهت بردار دوم ضرب برداری
در ضرب برداری قرار می گیرند همانند قسمت پ شکل . بنابراین سمت گیری دست ( روی صفحه کتاب یا صفحه نمایش) به گونه ای تنظیم می شود که انگشت ها بتوانند به راحتی بچرخند و در جهت بردار دوم ضرب برداری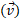 قرار گیرند شکل قسمت ت.
قرار گیرند شکل قسمت ت.
در نتیجه انگشت شست به حالت کشیده جهت نتیجه ضرب برداری را نشان خواهد داد. همانطور که در قسمت ث شکل نشان داده شده است این بردار در جهت مثبت محور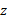 ( که در برون سوی صفحه شکل قرار دارد) با نتیجه پیشین سازگار است. قسمت ث شکل جهت
( که در برون سوی صفحه شکل قرار دارد) با نتیجه پیشین سازگار است. قسمت ث شکل جهت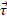 را نیز نشان می دهد که در جهت مثبت محور
را نیز نشان می دهد که در جهت مثبت محور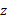 واقع است زیرا تکانه زاویه ای در آن جهت قرار دارد و بزرگی اش در حال افزایش یافتن است.
واقع است زیرا تکانه زاویه ای در آن جهت قرار دارد و بزرگی اش در حال افزایش یافتن است.
تکانه زاویه ای دستگاه ذرات
تکانه زاویه ای دستگاه ذرات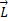 برابر با مجموع برداری تکانه های زاویه ای هریک از ذره هاست:
برابر با مجموع برداری تکانه های زاویه ای هریک از ذره هاست:
(13)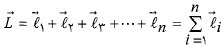
آهنگ زمانی تغییر این تکانه زاویه ای برابر با گشتاور نیروی خارجی برایند وارد شده به دستگاه ( مجموع برداری گشتاورهای ناشی از برهم کنش های ذرات دستگاه با ذرات خارج از دستگاه) است:
(14)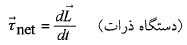
تکانه زاویه ای جسم صُلب
تکانه زاویه ای یک جسم صُلب که به دور محور ثابتی می چرخد، برابر با مولفه تکانه زاویه ای آن در راستای موازی با محوردوران است:
(15)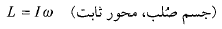
پایستگی تکانه زاویه ای
اگر گشتاور نیروی خارجی برایند وارد شده به یک دستگاه صفر باشد تکانه زاویه ای آن دستگاه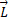 ثابت می ماند:
ثابت می ماند:
(16)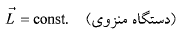
یا
(17)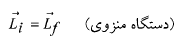
این معادلهقانون پایستگی تکانه زاویه ای را بیان می کند.
 مسئله نمونه- پایستگی تکانه، سوسک حمام بر روی قرص
مسئله نمونه- پایستگی تکانه، سوسک حمام بر روی قرص
در شکل مقابل یک سوسک حمام به جرم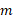 بر روی قرصی به جرم
بر روی قرصی به جرم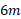 و شعاع
و شعاع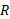 قرار دارد. قرص مانند یک چرخ و فلک با تندی زاویه ای
قرار دارد. قرص مانند یک چرخ و فلک با تندی زاویه ای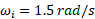 به دور محور مرکزی اش می چرخد. این سوسک در آغاز در شعاع
به دور محور مرکزی اش می چرخد. این سوسک در آغاز در شعاع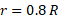 قرار دارد، اما بعد تا کناره قرص به برون سو می خزد. سوسک را مانند یک ذره در نظر بگیرید. در این صورت ، تندی زاویه ای آن چیست؟
قرار دارد، اما بعد تا کناره قرص به برون سو می خزد. سوسک را مانند یک ذره در نظر بگیرید. در این صورت ، تندی زاویه ای آن چیست؟
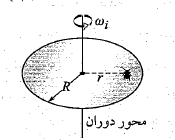
(1)خزیدن سوسک موجب می شود توزیع جرم ( و درنتیجه لختی دورانی) دستگاه سوسک-قرص تغییر کند. (2)تکانه زاویه ای دستگاه تغییر نمی کند زیرا هیچ گشتاور نیروی خارجی آن را تغییر نمی دهد. ( نیروها و گشتاورهای نیروی ناشی از خزیدن سوسک نسبت به دستگاه درونی هستند. (3) بزرگی تکانه زاویه ای یک جسم توپر یا یک ذره از معادله 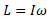 به دست می آید.
به دست می آید.
محاسبات:
ما می خواهیم تندی زاویه ای پایانی را پید کنیم. راه حل این است که تکانه زاویه ای پایانی 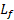 را با تکانه زاویه ای آغازی
را با تکانه زاویه ای آغازی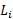 مساوی قرار دهیم، زیرا هر دو دارای تندی زاویه ای هستند. این کمیت هالختی دورانی
مساوی قرار دهیم، زیرا هر دو دارای تندی زاویه ای هستند. این کمیت هالختی دورانی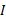 هم دارند. بنابراین ابتدا لختی دورانی دستگاه سوسک و قرص پیش و پس از خزیدن سوسک را پیدا می کنیم.
هم دارند. بنابراین ابتدا لختی دورانی دستگاه سوسک و قرص پیش و پس از خزیدن سوسک را پیدا می کنیم.
لختی دورانی قرص که به دور محور مرکزی اش می چرخد برابر با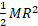 است. با قرار دادن
است. با قرار دادن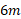 به جای جرم
به جای جرم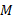 لختی دورانی قرص برابر است با
لختی دورانی قرص برابر است با
(1-1)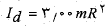
لختی دورانی سوسک حمام ( یک ذره) برابر با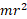 است.با قرار دادن شعاع مکان آغازی (
است.با قرار دادن شعاع مکان آغازی (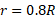 ) و شعاع مکان پایانی سوسک (
) و شعاع مکان پایانی سوسک (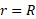 ) لختی دورانی آغازی آن را نسبت به محور دوران چنین به دستمی آوریم
) لختی دورانی آغازی آن را نسبت به محور دوران چنین به دستمی آوریم
(1-2)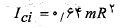
لختی دورانی پایانی سوسک نسبت به محور دوران برابر است با
(1-3)
بنابراین لختی دورانی آغازی دستگاه سوسک -قرص برابر است با
(1-4)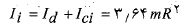
و برای لختی دورانی پایانی دستگاه داریم
(1-5)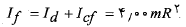
اکنون با این واقعیت که تکانه زاویه ای پایانی 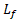 برابر با تکانه زاویه ای آغازی
برابر با تکانه زاویه ای آغازی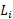 است از معادله
است از معادله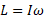 استفاده می کنیم و داریم
استفاده می کنیم و داریم
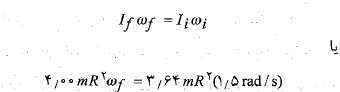
پس از حذف کرد مقادیر نامعلوم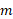 و
و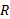 داریم
داریم
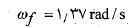
توجه کنید که تندی زاویه ای کاهش یافته است زیرا بخشی از جرم از محور دوران به برون سو حرکت کرده است در نتیجه لختی دورانی دستگاه افزایش یافته است.
حرکت تقدیمی ژیروسکوپ
ژیروسکوپ چرخان می تواند به دور یک محور قائم گذرنده از تکیه گاهش حرکت تقدیمی با آهنگ زیر انجام دهد
(18)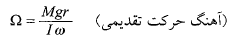
که در آن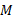 جرم ژیروسکوپ،
جرم ژیروسکوپ، 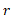 بازوی گشتاور،
بازوی گشتاور،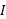 لختی دورانی و
لختی دورانی و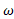 آهنگ چرخش است.
آهنگ چرخش است.
برای مطالعه مباحث بیشتر از محصول دوره آموزش فیزیک عمومی یک استفاده کنید.