مکان زاویه ای
برای توصیف دوران یک جسم صُلب به دور محور ثابت، که محور دوران نامیده می شود، یک خط مربع ثابت را در جسم، که بر محور عمود است و با جسم می چرخد در نظر می گیریم. مکان زاویه ای این خط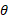 ، را نسبت به یک راستای ثابت اندازه گیری می کنیم. هرگاه
، را نسبت به یک راستای ثابت اندازه گیری می کنیم. هرگاه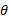 برحسب رادیان اندازه گیری شود داریم
برحسب رادیان اندازه گیری شود داریم
(1)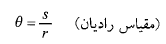
در این معادله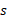 طول کمان مسیر دایره ای به شعاع
طول کمان مسیر دایره ای به شعاع 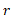 و زاویه
و زاویه 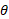 است. رابطه میان مقیاس رادیان با مقیاس زاویه ای عده دور و درجه چنین است
است. رابطه میان مقیاس رادیان با مقیاس زاویه ای عده دور و درجه چنین است
(2)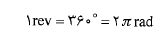
جابجایی زاویه ای
وقتی جسمی به دور محور دوران می چرخد و مکان زاویه ای آن از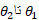 تغییر می کند، جابجایی زاویه ای زیر را انجام می د هد
تغییر می کند، جابجایی زاویه ای زیر را انجام می د هد
(3)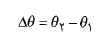
که در آن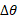 اگر دوران پادساعت گرد باشد، مثبت و اگر دوران ساعت گرد باشد منفی است.
اگر دوران پادساعت گرد باشد، مثبت و اگر دوران ساعت گرد باشد منفی است.
سرعت و تندی زاویه ای
اگر جسمی که می چرخد در بازه زمانی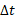 جابه جایی زاویه ای
جابه جایی زاویه ای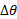 را انجام دهد، سرعت زاویه ای متوسط آن
را انجام دهد، سرعت زاویه ای متوسط آن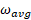 برابر است با
برابر است با
(4)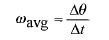
سرعت زاویه ای ( لحظه ای) جسم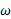 برابر است با
برابر است با
(5)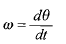
 و
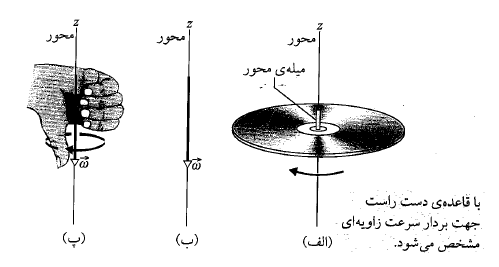
و هر دو بردارند و جهت شان از قاعده دست راست شکل زیر بدست می آید. این کمیت ها اگر دوران پادساعت گرد باشد مثبت، و اگر دوران ساعت گرد باشد منفی اند. بزرگی سرعت زاویه ای جسم تندی زاویه ای است.
هر دو بردارند و جهت شان از قاعده دست راست شکل زیر بدست می آید. این کمیت ها اگر دوران پادساعت گرد باشد مثبت، و اگر دوران ساعت گرد باشد منفی اند. بزرگی سرعت زاویه ای جسم تندی زاویه ای است.
شتاب زاویه ای
اکر سرعت زاویه ای جسمی در بازه زمانی از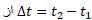 ω2تاω1تغییر کند، شتاب زاویه ای متوسط جسم
ω2تاω1تغییر کند، شتاب زاویه ای متوسط جسم 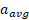 برابر است با
برابر است با
(6)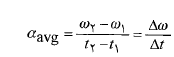
شتاب زاویه ای ( لحظه ای) جسم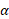 برابر است با
برابر است با
(7)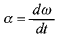
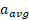 و
و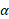 هر دو بردارند.
هر دو بردارند.
 مسئله نمونه- به دست آوردن سرعتزاویه ای از مکان زاویه ای
مسئله نمونه- به دست آوردن سرعتزاویه ای از مکان زاویه ای
قرص قسمت الف شکل مانند یک چرخ و فلک به دور محور مرکزی خود می چرخد.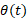 ، مکان زاویه ای مربوط به یک خط مرجع روی قرص از معادله زیر به دست می آید
، مکان زاویه ای مربوط به یک خط مرجع روی قرص از معادله زیر به دست می آید
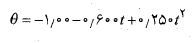
که در آن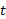 بر حسب ثانیه،
بر حسب ثانیه،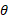 برحسب رادیان و مکان زاویه ای صفر در شکل مشخص شده است.
برحسب رادیان و مکان زاویه ای صفر در شکل مشخص شده است.
الف) نمودار مکان زاویه ای قرص را بر حسب زمان از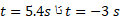 رسم کنید. نمودار وضعیت قرص و خط مرجع مکان زاویه ای آن را در زمان های
رسم کنید. نمودار وضعیت قرص و خط مرجع مکان زاویه ای آن را در زمان های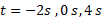 و در زمانی که نمودار محور
و در زمانی که نمودار محور را قطع می کند، رسم کنید.
را قطع می کند، رسم کنید.
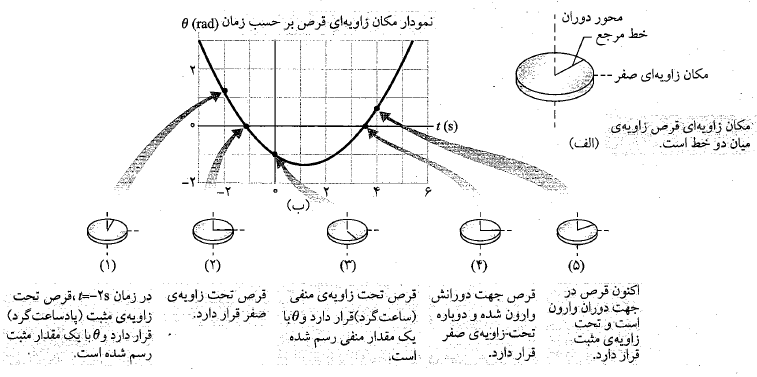
محاسبات: برای نشان دادن وضعیت قرص و خط مرجع آن در یک زمان خاص به تعیین در آن زمان نیاز داریم.
در آن زمان نیاز داریم.
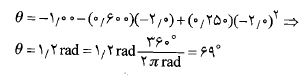
ب) در زمان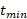 مقدار
مقدار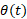 به کمینه نشان داده شده در قسمت ب شکل می رسد. این مقدار کمینه چقدر است؟
به کمینه نشان داده شده در قسمت ب شکل می رسد. این مقدار کمینه چقدر است؟
محاسبات: مشتق اول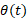 چنین به دست می آید
چنین به دست می آید
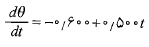
با مساوی صفر قرار دادن این مقدار و حل کردن معادله حاصل نسبت به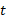 زمان مربوط به مقدار کمینه
زمان مربوط به مقدار کمینه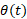 به دست می آید که برابر است با
به دست می آید که برابر است با
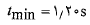
برای پیدا کردن کمینه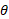 مقدار
مقدار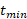 را در معادله قرار می دهیم
را در معادله قرار می دهیم
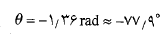
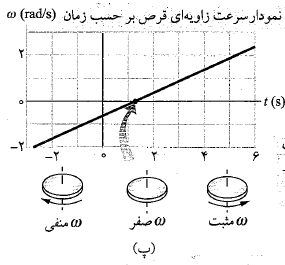
پ) نمودار سرعت زاویه ای قرص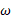 را بر حسب زمان از
را بر حسب زمان از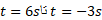 رسم کنید. وضعیت قرص را رسم کنید و جهت دوران آن و علامت
رسم کنید. وضعیت قرص را رسم کنید و جهت دوران آن و علامت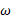 را در زمان های
را در زمان های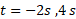 و نیز در زمان
و نیز در زمان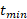 نشان دهید.
نشان دهید.
محاسبات: برای مشخص کردن وضعیت قرص در زمان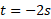 را در معادله
را در معادله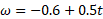 قرار می دهیم و مقدار زیر به دست می آید
قرار می دهیم و مقدار زیر به دست می آید
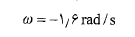
علامت منفی نشان می دهد که در زمان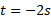 ، قرص به طور ساعت گرد می چرخد ( تصویر سمت چپ در قسمت پ شکل). با جانشانی
، قرص به طور ساعت گرد می چرخد ( تصویر سمت چپ در قسمت پ شکل). با جانشانی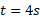 در معادله
در معادله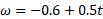 داریم
داریم
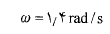
علامت مثبت نشان می دهد که اکنون قرص به طور پادساعت گرد می چرخد ( تصویر سمت راست قرص در قسمت پ شکل).
ت) با استفاده کردن از نتیجه های قسمت الف تا پ ، حرکت قرص را به ازای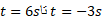 توصیف کنید.
توصیف کنید.
توصیف: وقتی ابتدا قرص را در زمان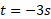 مشاهده می کنیم، می بینیم که مکان زاویه ای آن مثبت است، به طور ساعت گرد می چرخد، اما حرکتش در حال کند شدن است. قرص در مکان زاویه ای
مشاهده می کنیم، می بینیم که مکان زاویه ای آن مثبت است، به طور ساعت گرد می چرخد، اما حرکتش در حال کند شدن است. قرص در مکان زاویه ای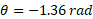 متوقف می شود سپس به طور پادساعت گرد شروع به چرخش می کند و مکان زاویه ای آن دوباره مثبت می شود.
متوقف می شود سپس به طور پادساعت گرد شروع به چرخش می کند و مکان زاویه ای آن دوباره مثبت می شود.
معادله های سینماتیکی مربوط به شتاب زاویه ای ثابت
حرکت با شتاب زاویه ای ثابت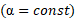 حالت ویژه ای ازحرکت دورانی است. معادله های سینماتیکی مربوط به این حالت به شرح زیر اند
حالت ویژه ای ازحرکت دورانی است. معادله های سینماتیکی مربوط به این حالت به شرح زیر اند
(8)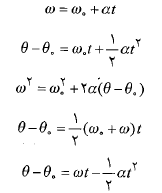
رابطه میان متغیرهای خطی و زاویه ای
نقطه ای از جسم صُلب چرخان واقع در فاصله از محور دوران در روی دایره ای به شعاع
از محور دوران در روی دایره ای به شعاع حرکتمی کند. اگر این جسم به اندازه زاویه
حرکتمی کند. اگر این جسم به اندازه زاویه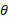 بچرخد، نقطه مورد نظر کمانی به طول
بچرخد، نقطه مورد نظر کمانی به طول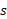 می پیماید که از معادله زیر بدست می آید.
می پیماید که از معادله زیر بدست می آید.
(9)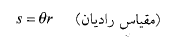
در این معادله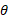 بر حسب رادیان است.
بر حسب رادیان است.
سرعت خطی نقطه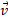 ، بر دایره مسیر مماس است؛ تندی خطی
، بر دایره مسیر مماس است؛ تندی خطی برابر است با
برابر است با
(10)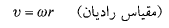
که در آن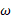 تندی زاویه ای جسم ( بر حسب رادیان بر ثانیه) است. شتاب خطی نقطه
تندی زاویه ای جسم ( بر حسب رادیان بر ثانیه) است. شتاب خطی نقطه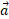 ، دو مولفه مماسی و شعاعی دارد. مولفه مماسی برابر است با
، دو مولفه مماسی و شعاعی دارد. مولفه مماسی برابر است با
(11)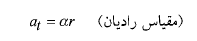
که در آن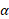 بزرگی شتاب زاویه ای جسم (بر حسب رادیان بر مجذور ثانیه) است. مولفه شعاعی شتاب
بزرگی شتاب زاویه ای جسم (بر حسب رادیان بر مجذور ثانیه) است. مولفه شعاعی شتاب 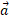 برابر است با
برابر است با
(12)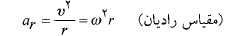
اگر نقطه ای حرکت دایره ای یکنواخت انجام دهد، دوره تناوب حرکت نقطه و جسم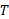 برابر است با
برابر است با
(13)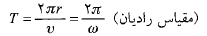
انرژی جنبشی دورانی و لختی دورانی
انرژی جنبشی یک جسم صُلب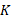 که به دور محور ثابتی می چرخد از معادله زیر به دست می آید
که به دور محور ثابتی می چرخد از معادله زیر به دست می آید
(14)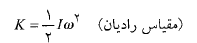
که در آن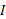 لختی دورانی جسم است. لختی دورانی برای دستگاه متشکل از ذره های مجزا به صورت زیر
لختی دورانی جسم است. لختی دورانی برای دستگاه متشکل از ذره های مجزا به صورت زیر
(15)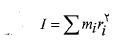
و برای جسم با توزیع جرم پیوسته به صورت زیر است
(16)
تعریف می شود. در این معادله ها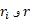 فاصله هر جزء جرم جسم تا محور دوران است و انتگرال روی کل جسم گرفته می شود، که در نتیجه هر جزء جرم را شامل می شود.
فاصله هر جزء جرم جسم تا محور دوران است و انتگرال روی کل جسم گرفته می شود، که در نتیجه هر جزء جرم را شامل می شود.
قضیه محورهای موازی
قضیه محورهای موازی لختی دورانی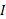 یک جسم نسبت به هر محور را به لختی دورانی همان جسم نسبت به یک محور موازی گذرنده ازمرکز جرم جسم ربط می دهد.
یک جسم نسبت به هر محور را به لختی دورانی همان جسم نسبت به یک محور موازی گذرنده ازمرکز جرم جسم ربط می دهد.
(17)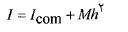
در این معادله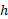 فاصله میان دو محور و
فاصله میان دو محور و لختی دورانی جسم نسبت به محور گذرنده از
لختی دورانی جسم نسبت به محور گذرنده از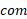 است. ما می توانیم
است. ما می توانیم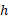 را به صورت فاصله محور دوران واقعی از محور دوران گذرنده از
را به صورت فاصله محور دوران واقعی از محور دوران گذرنده از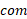 توصیف کنیم.
توصیف کنیم.
 مسئله نمونه- لختی دورانی یک دستگاه دو ذره ای
مسئله نمونه- لختی دورانی یک دستگاه دو ذره ای
قسمت الف شکل زیر یک جسم صُلب شامل دو ذره هریک به جرم را نشان می دهد که با میله ای به طول
را نشان می دهد که با میله ای به طول  و جرم ناچیز به هم وصل شده اند.
و جرم ناچیز به هم وصل شده اند.
الف) لختی دورانی جسم و نسبت به محور گذرنده از مرکز جرم و عمود بر میله مطابق شکل چیست؟
نسبت به محور گذرنده از مرکز جرم و عمود بر میله مطابق شکل چیست؟
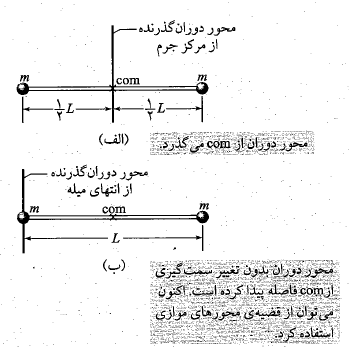
محاسبات:برای دو ذره که فاصله هر کدام از محور دوران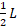 است داریم
است داریم
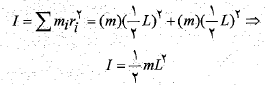
ب) لختی دورانی جسم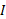 نسبت به محور گذرنده از انتهای چپ میله و موازی با محور اول قسمت ب شکل چیست؟
نسبت به محور گذرنده از انتهای چپ میله و موازی با محور اول قسمت ب شکل چیست؟
روش اول: مقدار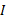 را مانند قسمت الف حساب می کنیم با این تفاوت که فاصله
را مانند قسمت الف حساب می کنیم با این تفاوت که فاصله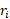 برای جرم سمت چپ صفر و برای جرم سمت راست
برای جرم سمت چپ صفر و برای جرم سمت راست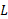 است. اکنون داریم
است. اکنون داریم
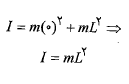
روش دوم: چون  نسبت به محور گذرنده ازمرکز جرم معلوم و محور مورد نظر با « محور مرکز جرم» موازی است، می توان از قضیه محورهای موازی استفاده کرد. در نتیجه داریم
نسبت به محور گذرنده ازمرکز جرم معلوم و محور مورد نظر با « محور مرکز جرم» موازی است، می توان از قضیه محورهای موازی استفاده کرد. در نتیجه داریم
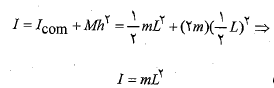
 مسئله نمونه- لختی دورانی یک میله یکنواخت با انتگرال گیری
مسئله نمونه- لختی دورانی یک میله یکنواخت با انتگرال گیری
شکل زیر یک میله یکنواخت باریک به جرم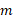 و طول
و طول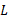 را بر روی محور
را بر روی محور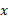 نشان می دهد که در آن مبدا مختصات در وسط میله قرار دارد.
نشان می دهد که در آن مبدا مختصات در وسط میله قرار دارد.
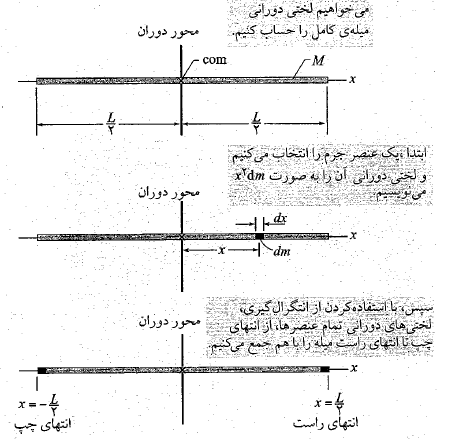
الف) لختی دورانی این میله نسبت به محور عمودی گذرنده از مرکز جرم چیست؟
محاسبات: چون میله یکنواخت است، نسبت جرم به طول برای تمام عنصرها و برای کل میله یکسان است.
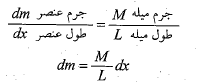
سپس انتگرال را از یک سر تا سر دیگر میله می گیریم تا تمام عنصرها را در بر بگیرد.
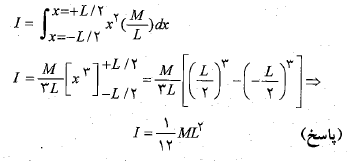
ب) لختی دورانی میله نسبت به یک محور جدید که عمود بر میله و گذرنده از انتها چپ میله است، چیست؟
نسبت به یک محور جدید که عمود بر میله و گذرنده از انتها چپ میله است، چیست؟
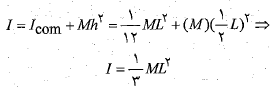
در واقع این نتیجه برای هر محور گذرنده از انتهای چپ یا راست و عمود بر میله صدق می کند.
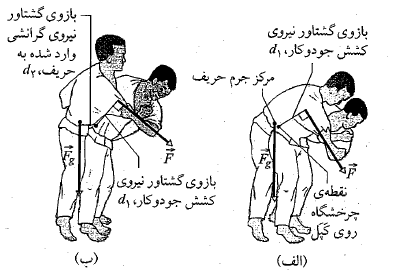
گشتاور نیرو
گشتاور نیرو بیان کننده اثر چرخانندگی یا پیچانندگی نیروی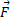 وارد شده به یک جسم نسبت به محور دوران است. اگر
وارد شده به یک جسم نسبت به محور دوران است. اگر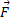 در نقطه ای با بردار مکان
در نقطه ای با بردار مکان نسبت به محور وارد شود بزرگی گشتاور نیرو برابر است با
نسبت به محور وارد شود بزرگی گشتاور نیرو برابر است با
(18)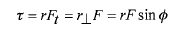
که در آن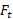 مولفه
مولفه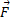 در راستای عمود بر
در راستای عمود بر 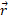 و
و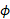 زاویه میان
زاویه میان و
و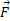 است. کمیت
است. کمیت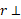 فاصله میان محور دوران و امتداد بردارF
فاصله میان محور دوران و امتداد بردارF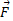 است. این امتداد را خط اثر
است. این امتداد را خط اثر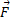 و
و 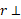 را بازوی گشتاور
را بازوی گشتاور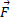 می نامند. به همین ترتیب
می نامند. به همین ترتیب هم بازوی گشتاور
هم بازوی گشتاور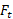 است.
است.
یکای گشتاور نیرو در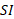 ، نیوتون – متر ( با نماد
، نیوتون – متر ( با نماد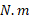 ) است. گشتاور نیروی
) است. گشتاور نیروی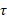 ، اگر جسم ساکن را به طور پادساعت گرد بچرخاند مثبت و اگر آن را به طور ساعت گرد بچرخاند منفی است.
، اگر جسم ساکن را به طور پادساعت گرد بچرخاند مثبت و اگر آن را به طور ساعت گرد بچرخاند منفی است.
قانون دوم نیوتون در شکل زاویه ای
قانون دوم نیوتون در حرکت دورانی به صورت زیر نوشته می شود
(19)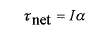
که در آن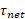 گشتاور نیروی برایند وارد شده به یک ذره یا یک جسم صُلب،
گشتاور نیروی برایند وارد شده به یک ذره یا یک جسم صُلب،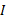 لختی دورانی ذره یا جسم نسبت به محور دوران و
لختی دورانی ذره یا جسم نسبت به محور دوران و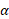 شتاب زاویه ای حاصل از دوران است.
شتاب زاویه ای حاصل از دوران است.
 مسئله نمونه – قانون دوم نیوتون، دوران ، گشتاور نیرو، قرص
مسئله نمونه – قانون دوم نیوتون، دوران ، گشتاور نیرو، قرص
شکل زیر قسمت الف قرص یکنواختی به جرم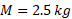 و شعاع
و شعاع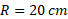 را نشان می دهد، که روی یک محور افقی ثابت نصب شدهاست. جسمی به جرم
را نشان می دهد، که روی یک محور افقی ثابت نصب شدهاست. جسمی به جرم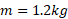 از یک ریسمان بی جرم پیچیده شده به دور قرص آویخته شده است. شتاب جسم در حال سقوط، شتاب زاویه ای قرص و نیروی کشش ریسمان را حساب کنید. ریسمان نمی لغزد و محور بی اصطکاک است.
از یک ریسمان بی جرم پیچیده شده به دور قرص آویخته شده است. شتاب جسم در حال سقوط، شتاب زاویه ای قرص و نیروی کشش ریسمان را حساب کنید. ریسمان نمی لغزد و محور بی اصطکاک است.
محاسبات:
نیروهای وارد شده به جسم: این نیروها در نموار جسم -آزاد مربوط به جسم در شکل زیر قسمت ب نشان داده شده اند. در این شکل، نیروی کشش ریسمان و
نیروی کشش ریسمان و نیروی گرانشی با بزرگی
نیروی گرانشی با بزرگی است. اکنونقانون دوم نیوتون برای مولفه های مربوط به راستای محور قائم
است. اکنونقانون دوم نیوتون برای مولفه های مربوط به راستای محور قائم به صورت زیر نوشته می شود
به صورت زیر نوشته می شود
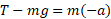
که در آن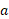 بزرگی شتاب ( به سمت پایین محور
بزرگی شتاب ( به سمت پایین محور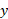 ) است. با استفاده کردن از این معادله نمی توان شتاب
) است. با استفاده کردن از این معادله نمی توان شتاب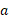 را به دست آورد، چون در آن کمیت نامعلوم
را به دست آورد، چون در آن کمیت نامعلوم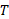 وجود دارد.
وجود دارد.
گشتاور نیروی وارد شده به قرص
پیش از توجه به محور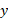 بهتر است محور
بهتر است محور 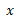 را در نظر بگیریم. در اینجا به دوران قرص توجه می کنیم. برای محاسبه گشتاورهای نیرو و لختی دورانی
را در نظر بگیریم. در اینجا به دوران قرص توجه می کنیم. برای محاسبه گشتاورهای نیرو و لختی دورانی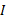 فرض می کنیم محور دوران بر قرص عمود است و از مرکز قرص نقطه
فرض می کنیم محور دوران بر قرص عمود است و از مرکز قرص نقطه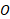 در قسمت پ شکل می گذرد.
در قسمت پ شکل می گذرد.

گشتاورهای نیرو از معادله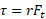 به دست می آیند. نیروی گرانشی وارد شده به قرص و نیروی وارد شده به قرص از سوی محور، هر دو در مرکز قرص یعنی در فاصله
به دست می آیند. نیروی گرانشی وارد شده به قرص و نیروی وارد شده به قرص از سوی محور، هر دو در مرکز قرص یعنی در فاصله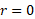 اثر می کنند و در نتیجه گشتاورهای آن ها صفر است.
اثر می کنند و در نتیجه گشتاورهای آن ها صفر است.
نیروی وارد شده به قرصT از سوی ریسمان در فاصلهr=R
از سوی ریسمان در فاصلهr=R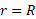 اثر می کند و بر کناره قرص مماس است. گشتاور این نیرو
اثر می کند و بر کناره قرص مماس است. گشتاور این نیرو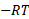 است. دلیل علامت منفی این است که گشتاور این نیرو قرص را از حال سکون به طور ساعت گرد می چرخاند. لختی دورانی قرص
است. دلیل علامت منفی این است که گشتاور این نیرو قرص را از حال سکون به طور ساعت گرد می چرخاند. لختی دورانی قرص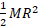 است. پس رابطه
است. پس رابطه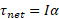 را می توان به صورت زیر نوشت
را می توان به صورت زیر نوشت
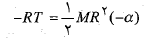
این معادله بی فایده به نظر می رسد زیرا شامل دو کمیت نامعلوم 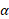 و
و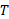 است که هیچ یک کمیت مورد نظر
است که هیچ یک کمیت مورد نظر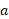 نیست. با این حال معادله با استفاده کردن از راه های فیزیکی می تواند مفید واقع شود. چون ریسمان نمی لغزد ، شتاب خطی جسم
نیست. با این حال معادله با استفاده کردن از راه های فیزیکی می تواند مفید واقع شود. چون ریسمان نمی لغزد ، شتاب خطی جسم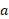 با شتاب خطی (مماسی) کناره قرص
با شتاب خطی (مماسی) کناره قرص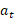 برابر است. بنابراین با توجه به معادله
برابر است. بنابراین با توجه به معادله 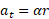 نتیجه می گیریم که
نتیجه می گیریم که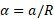 . با جانشانی این مقدار در در معادله بالا داریم
. با جانشانی این مقدار در در معادله بالا داریم
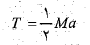
ترکیب کردن نتیجه ها: اکنون معادله های گفته شده را ترکیب می کنیم، داریم
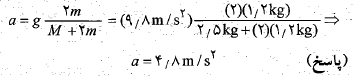
حال برای پید کردن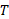 داریم
داریم
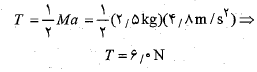
شتاب جسم در حال سقوط کمتر از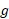 و نیروی کشش ریسمان (مساوی با
و نیروی کشش ریسمان (مساوی با 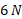 ) کمتر از نیروی گرانشی وارد شده به جسم آویخته شده
) کمتر از نیروی گرانشی وارد شده به جسم آویخته شده 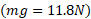 است. در ضمن شتاب جسم و نیروی کشش ریسمان به جرم قرص بستگی دارند، اما به شعاع قرص بستگی ندارند.
است. در ضمن شتاب جسم و نیروی کشش ریسمان به جرم قرص بستگی دارند، اما به شعاع قرص بستگی ندارند.
مشاهده می کنیم که فرمول های به دست آمده در بالا در حالت بی جرم بودن قرص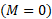 نتیجه
نتیجه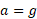 و
و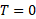 را پیشگویی می کنند. این نتیجه قابل انتظار است چون در این حالت جسم مانند یک جسم آزاد سقوط می کند و ریسمان را به دنبال خود می کشد. شتاب زاویه ای قرص چنین بدست می آید
را پیشگویی می کنند. این نتیجه قابل انتظار است چون در این حالت جسم مانند یک جسم آزاد سقوط می کند و ریسمان را به دنبال خود می کشد. شتاب زاویه ای قرص چنین بدست می آید
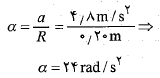
کار و انرژی جنبشی دورانی
معادله های مورد استفاده در محاسبه کار و توان در حرکت دورانی، با معادله های مورد استفاده در حرکت انتقالی متناظراند و عبارت اند از
(20)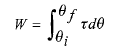
(21)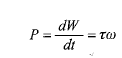
وقتی 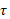 ثابت است، معادله (20) به صورت زیر ساده می شود
ثابت است، معادله (20) به صورت زیر ساده می شود
(22)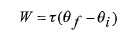
معادله مربوط بهقضیه کار و انرژی جنبشی که برای اجسام چرخان به کار می رود چنین است.
(23)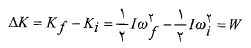
 مسئله نمونه- کار و انرژی جنبشی دورانی، گشتاور نیرو ، قرص
مسئله نمونه- کار و انرژی جنبشی دورانی، گشتاور نیرو ، قرص
فرض می کنیم قرص شکل زیر در زمان 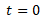 از حال سکون شروع به دوران می کند. همچنین فرض می کنیم نیروی کش ریسمان بی جرم
از حال سکون شروع به دوران می کند. همچنین فرض می کنیم نیروی کش ریسمان بی جرم 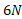 و شتاب زاویه ای قرص
و شتاب زاویه ای قرص 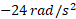 باشد. انرژی جنبشی دورانی قرص
باشد. انرژی جنبشی دورانی قرص 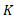 در زمان
در زمان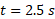 چقدر است؟
چقدر است؟
محاسبات : چون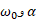 ( مساوی با صفر) را می دانیم و می خواهیم
( مساوی با صفر) را می دانیم و می خواهیم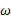 را به دست آوریم
را به دست آوریم
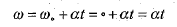
با جانشانی کمیت های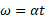 و
و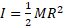 داریم
داریم
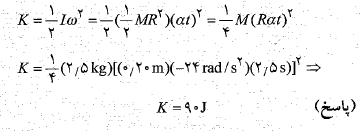
برای مطالعه مباحث بیشتر از محصول دوره آموزش فیزیک عمومی یک استفاده کنید.