حرکت شناسی
دنیا و هرچه در آن است در حال حرکت است؛ حتی اشیای به ظاهر ساکن، مانند یک جاده، چرخش زمین به دور خود، حرکت مداری زمین به دور خورشید، حرکت مداری خورشید به دور مرکز کهکشان را ه شیری و حرکت این کهکشان نسبت به کهکشان های دیگر، نیز حرکت می کنند. رده بندی و مقایسه ی حرکت ( حرکت شناسی یا سینماتیک نام دارد) اغلب کاری چالش برانگیز است.
برخی ویژگی های کلی حرکت شامل
1.حرکت فقط در طول یک خط راست انجام می شود. این خط ممکن است در راستای قائم، در راستای افقی یا به صورت مورب باشد، اما باید راست باشد.
2.نیروها (هُل دادن ها و کشیدن ها) باعث ایجاد حرکت می شوند.
2.شیء در حالت حرکت یک ذره است ( منظور شیئی نقطه مانند نظیرالکترون است) یا شیئی است که مانند یک ذره حرکت می کند( بدین گونه که تمام اجزاء آن در یک جهت و با یک آهنگ حرکت می کنند). یک قطعه ی چدن خشک را که از بالای یک سطح شیب دار به پایین می لغزد، می توان یک ذره ی در حال حرکت در نظر گرفت؛ اما بوته ی خاری که در حال وول خوردن به پایین است نمی توان یک ذره فرض کرد.
مکان و جابجایی
تعیین مکان یک شیء به معنی پیدا کردن موضع شیء نسبت به یک نقطه ی مرجع است، که اغلب، مبداء (یا نقطه ی صفر) محوری مانند محور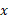 ، مانند شکل زیر. جهت مثبت این محور همان جهت افزایش یافتن عددها ( مختصه ها) است، که در شکل به سمت راست است، و جهت مخالف، جهت منفی است.
، مانند شکل زیر. جهت مثبت این محور همان جهت افزایش یافتن عددها ( مختصه ها) است، که در شکل به سمت راست است، و جهت مخالف، جهت منفی است.
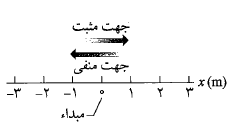
برای مثال، یک ذره ممکن است در مکان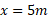 باشد، که نشان می دهد ذره در فاصله 5 متری طرف مثبت مبداء واقع شده است. اگر ذره در مکان
باشد، که نشان می دهد ذره در فاصله 5 متری طرف مثبت مبداء واقع شده است. اگر ذره در مکان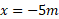 باشد، معنی اش این است که به همان فاصله در سوی مخالف مبداء واقع است. در روی محورx ، مختصه-5m از مختصه
باشد، معنی اش این است که به همان فاصله در سوی مخالف مبداء واقع است. در روی محورx ، مختصه-5m از مختصه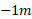 کوچک تر است و هر دو از مختصه
کوچک تر است و هر دو از مختصه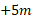 کوچک ترند. نوشتن علامت مثبت مختصه لازم نیست، اما علامت منفی را همیشه باید نوشت.
کوچک ترند. نوشتن علامت مثبت مختصه لازم نیست، اما علامت منفی را همیشه باید نوشت.
تغییر مکان ذره از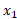 به مکان دیگر
به مکان دیگر 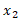 را جابه جایی
را جابه جایی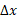 ، می نامند، که برابر است با
، می نامند، که برابر است با

( نماد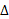 ، حرف یونانی دلتای بزرگ است، که نشان دهنده ی تغییر یک کمیت و معرف مقدار پایانی (نهایی) منهای مقدار آغازی (اولی) کمیت است). هنگامی که عددهای مربوط به مکان های
، حرف یونانی دلتای بزرگ است، که نشان دهنده ی تغییر یک کمیت و معرف مقدار پایانی (نهایی) منهای مقدار آغازی (اولی) کمیت است). هنگامی که عددهای مربوط به مکان های 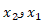 را در معادله
را در معادله 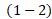 قرار می دهیم، حاصل مثبت همیشه نشان می دهد که جابه جایی در جهت مثبت ( در شکل بالا به راست سو) و حاصل منفی نشان می دهد که جابه جایی در جهت مخالف ( در شکل بالا به چپ سو) است.
قرار می دهیم، حاصل مثبت همیشه نشان می دهد که جابه جایی در جهت مثبت ( در شکل بالا به راست سو) و حاصل منفی نشان می دهد که جابه جایی در جهت مخالف ( در شکل بالا به چپ سو) است.
به عنوان مثال، اگر ذره از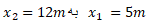 حرکت کند،
حرکت کند، 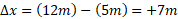 خواهد بود. این نتیجه مثبت نشان م یدهد که حرکت در جهت مثبت صورت گرفته است. حال اگر ذره از
خواهد بود. این نتیجه مثبت نشان م یدهد که حرکت در جهت مثبت صورت گرفته است. حال اگر ذره از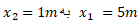 حرکت کند، در آن صورت
حرکت کند، در آن صورت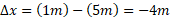 خواهد بود. این نتیجه منفی نشان می دهد که حرکت در جهت منفی صورت گرفته است.
خواهد بود. این نتیجه منفی نشان می دهد که حرکت در جهت منفی صورت گرفته است.
عدد واقعی مترهای پیموده شده در طی مسافت به جابه جایی ربطی ندارد؛ جابه جایی فقط مربوط به مکان های آغازی و پایانی حرکت است. به عنوان مثال، اگر ذره از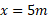 به
به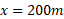 برود و دوباره به
برود و دوباره به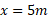 برگردد، جابه جایی از آغاز تا پایان برابر است با
برگردد، جابه جایی از آغاز تا پایان برابر است با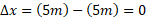 .
.
علامت ها
علامت مثبت برای جابه جایی نیازی به نشان دادن ندارد، اما علامت منفی ر همیشه باید نشان داد. اگر علامت ( و در نتیجه جهت) جا به جایی را نادیده بگیریم، فقط بزرگی ( یا قدر مطلق) جابه جایی مشخص می شود. برای مثال، جابه جایی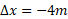 دارای بزرگی
دارای بزرگی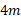 است.
است.
جابه جایی نمونه ای از کمیت برداری است، که کمیتی دارای جهت و بزرگی، هر دو، است. در اینجا کافی است بدانیم که جابه جایی دو ویژگی دارد (1) بزرگی، که مسافت (مثلا تعداد مترهای) بین مکان های آغازی و پایانی است. (2) جهت ، که از مکان آغازی به سمت مکان پایانی است، و اگر حرکت در راستای یک محور صورت گیرد، جهت با علامت مثبت یا منفی نشان داده می شود.
 خودآزمایی 1
خودآزمایی 1
در اینجا سه زوج مکان های آغازی و پایانی در راستای محور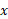 ، به ترتیب مشخص شده اند. (الف)
، به ترتیب مشخص شده اند. (الف)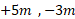 (ب)
(ب)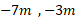 (پ)
(پ)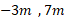 . جابه جایی مربوط به کدام زوج ها منفی است؟
. جابه جایی مربوط به کدام زوج ها منفی است؟
سرعت متوسط و تندی متوسط
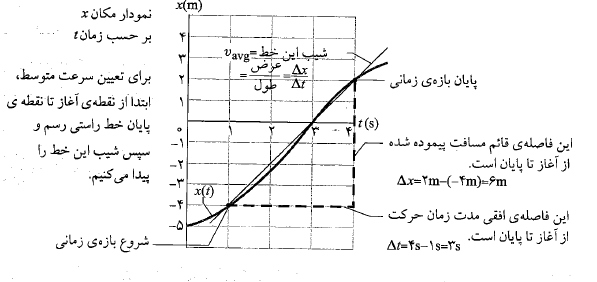
برای توصیف مکان، یک روش ساده استفاده کردن از نمودار مکان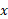 به صورت تابعی از زمان
به صورت تابعی از زمان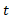 ، یعنی نمودار
، یعنی نمودار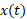 است ( نمادگذاری
است ( نمادگذاری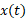 به معنی
به معنی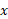 تابعی از
تابعی از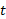 است، نه حاصل ضرب
است، نه حاصل ضرب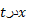 ). به عنوان مثالی ساده، در شکل زیر تابع
). به عنوان مثالی ساده، در شکل زیر تابع 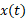 مربوط به یک حیوان گورکن در حال سکون ( که آن را یک ذره در نظر می گیریم) در بازه زمانی 7 ثانیه را نشان می دهد. این حیوان در مختصه
مربوط به یک حیوان گورکن در حال سکون ( که آن را یک ذره در نظر می گیریم) در بازه زمانی 7 ثانیه را نشان می دهد. این حیوان در مختصه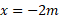 ساکن است.
ساکن است.
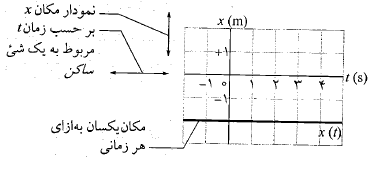
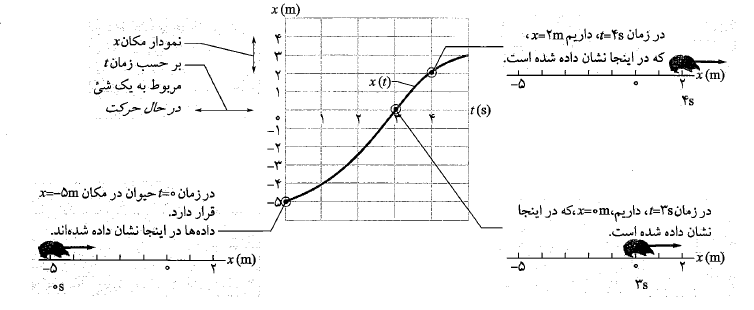
شکل زیر برای حیوان رسم شده و جالب تر است، زیرا به حرکت مربوط می شود. گورکن ابتدا در زمان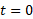 در مکان
در مکان 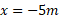 قرار دارد. سپس به سوی مکان
قرار دارد. سپس به سوی مکان 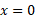 حرکت می کند، در زمان
حرکت می کند، در زمان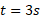 از آن نقطه می گذرد، و آنگاه به سمت مقادیر مثبت و بزرگ تر
از آن نقطه می گذرد، و آنگاه به سمت مقادیر مثبت و بزرگ تر 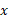 حرکت می کند. شکل زیر حرکت راست خط واقعی گورکن را هم ( در سه زمان) نشان می دهد و شبیه ان چیزی است که می توانیم ببینیم. نمودار شکل انتزاعی تر است، اما نشان می دهد که گورکن با چه سرعتی حرکت می کند.
حرکت می کند. شکل زیر حرکت راست خط واقعی گورکن را هم ( در سه زمان) نشان می دهد و شبیه ان چیزی است که می توانیم ببینیم. نمودار شکل انتزاعی تر است، اما نشان می دهد که گورکن با چه سرعتی حرکت می کند.
در عمل، در حرکت ذره اصطلاح«با چه سرعتی» به چند کمیت وابسته است. یکی از این کمیت ها سرعت متوسط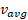 ، است که برابر با نسبت جابه جایی انجام شده
، است که برابر با نسبت جابه جایی انجام شده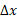 ، به بازه ی زمانی خاص
، به بازه ی زمانی خاص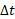 است:
است:

این نماد گذاری نشان می دهد که مکان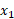 مربوط به زمان
مربوط به زمان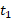 و مکان
و مکان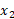 مربوط به زمان
مربوط به زمان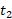 است. یکای معمول برای
است. یکای معمول برای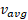 ، متر بر ثانیه ( با نماد
، متر بر ثانیه ( با نماد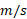 ) است.
) است.
نمودارها. در نمودار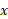 برحسب
برحسب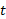 ،
،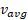 شیب خط راستی است که دو نقطه خاص از منحنی
شیب خط راستی است که دو نقطه خاص از منحنی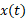 را به هم وصل می کند؛ یکی از نقطه ها متناظر با
را به هم وصل می کند؛ یکی از نقطه ها متناظر با 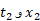 ، و نقطه دیگر متناظر با
، و نقطه دیگر متناظر با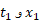 است.
است.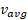 نیز مانند جابه جایی دارای بزرگی و جهت است ( یعنی کمیتی برداری است). بزرگی
نیز مانند جابه جایی دارای بزرگی و جهت است ( یعنی کمیتی برداری است). بزرگی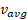 ، همان بزرگی خط راست است. مثبت بودن
، همان بزرگی خط راست است. مثبت بودن 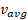 و ( شیب خط) نشان می دهد که خط به بالا سو و به سمت راست کشیده می شود و منفی بودن
و ( شیب خط) نشان می دهد که خط به بالا سو و به سمت راست کشیده می شود و منفی بودن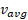 و ( شیب خط) نمایشگر آن است که خط به پایین سو و به سمت راست کشیده می شود.
و ( شیب خط) نمایشگر آن است که خط به پایین سو و به سمت راست کشیده می شود.
سرعت متوسط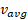 همیشه با جابه جایی
همیشه با جابه جایی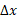 هم علانت است، زیرا در معادله (2-2) ،
هم علانت است، زیرا در معادله (2-2) ،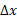 همیشه مثبت است. شکل زیر چگونگی پیدا کردن
همیشه مثبت است. شکل زیر چگونگی پیدا کردن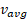 جیوان گورکن با استفاده کردن از شکل فوق و در بازه زمانی
جیوان گورکن با استفاده کردن از شکل فوق و در بازه زمانی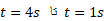 را نشان می دهد. در این شکل نقطه ای از منحنی مکان را که مربوط به آغاز بازه زمانی است، با یک خط راست به نقطه دیگر که مربوط به پایان بازه زمانی است وصل می کنیم. سپس شیب
را نشان می دهد. در این شکل نقطه ای از منحنی مکان را که مربوط به آغاز بازه زمانی است، با یک خط راست به نقطه دیگر که مربوط به پایان بازه زمانی است وصل می کنیم. سپس شیب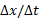 این خط راست را پیدا می کنیم. به ازای بازه زمانی داده شده سرعت متوسط برابر است با
این خط راست را پیدا می کنیم. به ازای بازه زمانی داده شده سرعت متوسط برابر است با
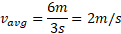
تندی متوسط 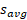 ، کمیت دیگر است که «چگونه تند رفتن » را در حرکت یک ذره توصیف می کند. در حالی که سرعت متوسط به جابه جایی
، کمیت دیگر است که «چگونه تند رفتن » را در حرکت یک ذره توصیف می کند. در حالی که سرعت متوسط به جابه جایی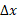 ذره مربوط می شود، تندی متوسط به مسافت کل پیموده شده ( مثلا عده ی مترهای پیموده شده) بستگی دارد و از جهت حرکت مستقل است یعنی
ذره مربوط می شود، تندی متوسط به مسافت کل پیموده شده ( مثلا عده ی مترهای پیموده شده) بستگی دارد و از جهت حرکت مستقل است یعنی

چون تندی متوسط به جهت بستگی ندارد، بدون علامت جبری است. گاهی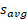 همان
همان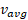 (بدون توجه به علامت ) است، اما این مقدار می توانند کاملا متفاوت باشند.
(بدون توجه به علامت ) است، اما این مقدار می توانند کاملا متفاوت باشند.
 مسئله نمونه1
مسئله نمونه1
فرض کنید در جاده مستقیمی با یک خودرو وانت فرسوده مسافت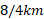 را با تندی
را با تندی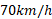 می پیمایید. در این حال بنزین وانت تمام می شود و خودرو می ایستد. از این به بعد مسافت
می پیمایید. در این حال بنزین وانت تمام می شود و خودرو می ایستد. از این به بعد مسافت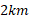 را در مدت 30 دقیقه با پای پیاده و در همان جاده پیش می روید تا به جایگاه پخش بنزین برسید.
را در مدت 30 دقیقه با پای پیاده و در همان جاده پیش می روید تا به جایگاه پخش بنزین برسید.
الف) جابه جایی کل شما از لحظه شروع به رانندگی تا رسیدن به جایگاه پخش بنزین چقدر است؟
حل: با استفاده از معادله (1-2) داریم
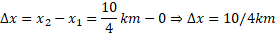
بنابراین جابه جایی کل شما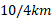 در جهت مثبت محور
در جهت مثبت محور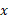 است.
است.
ب)بازه زمانی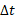 از آغاز حرکت شما با خودرو تا رسیدن به جایگاه پخش بنزین چقدر است؟
از آغاز حرکت شما با خودرو تا رسیدن به جایگاه پخش بنزین چقدر است؟
حل: ابتدا می نویسیم
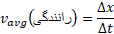
با مرتب کردن این رابطه و جانشانی داده ها داریم
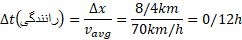
پس می توان نوشت
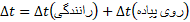
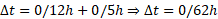
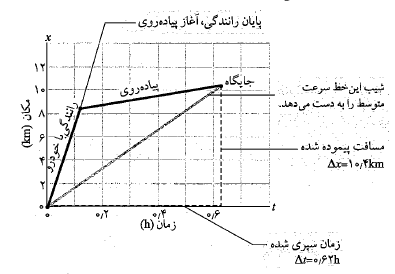
پ) سرعت متوسط شما،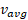 از آغاز رانندگی تا رسیدن به چایگاه پخش بنزین چقدر است> این مقدار را به روش های عددی و ترسیمی به دست آورید.
از آغاز رانندگی تا رسیدن به چایگاه پخش بنزین چقدر است> این مقدار را به روش های عددی و ترسیمی به دست آورید.
حل: در اینجا داریم
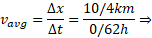
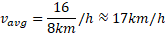
برای پیدا کردن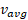 به روش ترسیمی ابتدا تابع
به روش ترسیمی ابتدا تابع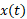 را مطابق شکل رسم می کنیم. دراین شکل نقطه اغاز حرکت در مبداء مختصات و نقطه پایان در نمودار نقطه مشخص شده با «جایگاه» است. سرعت متوسط شما از شیب خط راست وصل کننده این دو نقطه یعنی از تقسیم کردن عرض نقطه مشخص شده با «جایگاه» (
را مطابق شکل رسم می کنیم. دراین شکل نقطه اغاز حرکت در مبداء مختصات و نقطه پایان در نمودار نقطه مشخص شده با «جایگاه» است. سرعت متوسط شما از شیب خط راست وصل کننده این دو نقطه یعنی از تقسیم کردن عرض نقطه مشخص شده با «جایگاه» (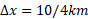 ) به طول این نقطه (
) به طول این نقطه (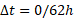 ) به دست می آید که برابر است با
) به دست می آید که برابر است با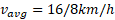 .
.
ت) فرض کنید پس از گرفتن بنزین از جایگاه 45 دقیقه دیگر طول بکشد تا شما به خودرو خود برگردید. تندی متوسط شما از آغاز رانندگی تا بازگشت دوباره به خودرو چقدر است؟
حل: مسافت کل برابر است با
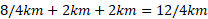
و بازه زمانی کل برابر است با
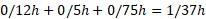
بنابراین با استفاده کردن از معادله (3-2) داریم
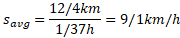
حرکت دو بُعدی
مطالعه جرکت دوبُعدی را با معرفی مکان و جابه جایی آغاز می کنیم.
مکان و جابه جایی
یکی از راه های کلی برای تعیین مکان یک ذره استفاده کردن ازبُرد مکان است، که از یک نقطه مرجع ( بطور معمول مبداء یکدستگاه مختصات) تا مکان ذره رسم می شود. با استفاده کردن از نماد گذاری بردارهای یکه در پودمان 3-2 می توانr را به صورت زیر نشان داد
است، که از یک نقطه مرجع ( بطور معمول مبداء یکدستگاه مختصات) تا مکان ذره رسم می شود. با استفاده کردن از نماد گذاری بردارهای یکه در پودمان 3-2 می توانr را به صورت زیر نشان داد

که در آن 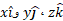 مولفه های برداری و ضریب های
مولفه های برداری و ضریب های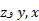 مولفه های نرده ای بردار
مولفه های نرده ای بردار هستند. ضریب های
هستند. ضریب های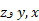 ، مکان ذره را در طول محورهای مختصات نسبت به مبداء مشخص می کنند؛ یعنی ذره دارای مختصات راست گوشه ای (
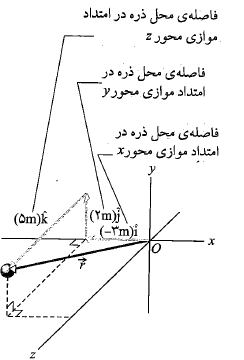
، مکان ذره را در طول محورهای مختصات نسبت به مبداء مشخص می کنند؛ یعنی ذره دارای مختصات راست گوشه ای (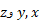 ) است. برای مثال شکل زیرذره ای را با بردار مکان
) است. برای مثال شکل زیرذره ای را با بردار مکان
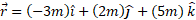
و مختصات راست گوشه ای (5m,2m , -3m ) نشان می دهد. ذره در طول محور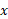 به فاصله 3m از مبداء در جهت
به فاصله 3m از مبداء در جهت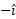 در طول محور
در طول محور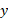 به فاصله2m از مبداء در جهت
به فاصله2m از مبداء در جهت و در طول محور
و در طول محور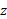 به فاصله5m از مبداء در جهت
به فاصله5m از مبداء در جهت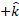 قرار دارد.
قرار دارد.
هنگامی که ذره حرکت می کند بردار مکان به گونه ای تغییر می کند که راستای بردار همیشه از نقطه مرجع(مبداء)تا مکان ذره است. اگر بردار مکان مثلا از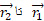 در یک بازه زمانی معین تغییر کند، جابه جایی ذره در آن بازه زمانی
در یک بازه زمانی معین تغییر کند، جابه جایی ذره در آن بازه زمانی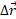 برابر است با
برابر است با

استفاده کردن از نمادگذاری بردارهای یکه در معادله (1-4) این جابه جایی را می توان به صورت زیر نمایش داد
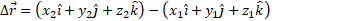
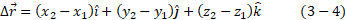
که در آن مختصاتx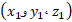 مربوط به بردار مکان
مربوط به بردار مکان 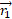 و مختصات
و مختصات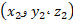 مربوط به بردار مکان
مربوط به بردار مکان 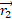 است. با قرار دادن
است. با قرار دادن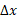 به جای
به جای 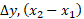 به جای
به جای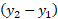 و
و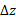 به جای
به جای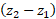 ، بردار جابه جایی را به صورت زیر هم می توان نوشت:
، بردار جابه جایی را به صورت زیر هم می توان نوشت:
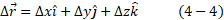
 مسئله نمونه2: بردار مکان دوبُعدی، دویدن خرگوش
مسئله نمونه2: بردار مکان دوبُعدی، دویدن خرگوش
خرگوشی در محوطه ای که محورهای مختصات بر روی آن رسم شده اند می دود. مختصات مکان(به متر) خرگوش بر حسب زمان (به ثانیه) از رابطه های زیر به دست می آید
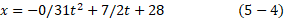
و
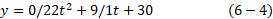
الف) در زمان 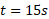 ، بردار مکان خرگوش
، بردار مکان خرگوش  ، با استفاده کردن از نمادگذاری بردارهای یکه و نمادگذاری بزرگی -زاویه چیست؟
، با استفاده کردن از نمادگذاری بردارهای یکه و نمادگذاری بزرگی -زاویه چیست؟
حل: می توان نوشت
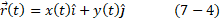
( به جای ،
،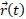 نوشته ایم زیرا مولفه ها و در نتیجه
نوشته ایم زیرا مولفه ها و در نتیجه تابع
تابع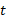 هستند.)
هستند.)
در زمان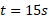 موله های نرده ای عبارت اند از
موله های نرده ای عبارت اند از
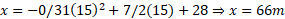
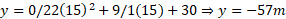
بنابراین در زمان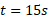 داریم
داریم
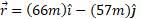
این بردار در شکل زیر قسمت الف رسم شده است.
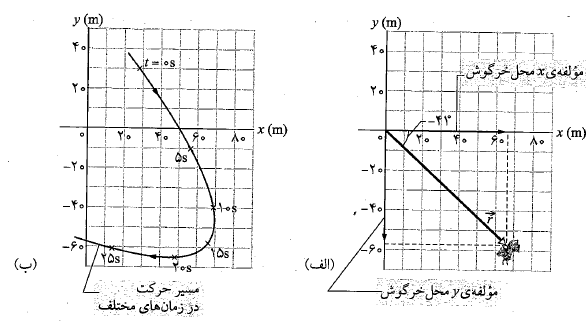
برای تعیین بزرگی و زاویه بردار توجه کنید که مولفه ها ضلع های یک مثلث راست گوشه و
توجه کنید که مولفه ها ضلع های یک مثلث راست گوشه و وتر آن مثلث است. بنابراین با استفاده کردن از معادله (3-6) می توان نوشت:
وتر آن مثلث است. بنابراین با استفاده کردن از معادله (3-6) می توان نوشت:
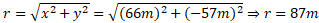
و
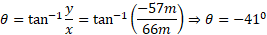
ب) مسیر خرگوش را برای زمان های 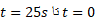 رسم کنید.
رسم کنید.
ترسیم نمودار: ما مکان خرگوش در یک زمان را مشخص کردیم، اما برای دیدن مسیر حرکت خرگوش به یک نمودار نیاز داریم. بنابراین قسمت (الف) را برای چند مقدار t تکرار و سپس نتیجه ها را به صورت نمودار رسم می کنیم. شکل بالا قسمت(ب) محل نقطه های مربوط به شش مقدارt و مسیر وصل کننده ی آن ها به یکدیگر را نشان می دهد.
برای مطالعه مباحث بیشتر ازمحصول دوره آموزشی فیزیک عمومی1 استفاده کنید.