مرور ریاضیات مورد استفاده در درس فیزیک عمومی 2: دستگاههای مختصات،المانگیری، مشتق و انتگرال
المانگیری صحیح در دستگاههای مختصات مختلف برای حل بسیاری از مسائلفیزیک2 که در آنها توزیع بار الکتریکی پیوسته وجود دارد امری ضروری است.
در این قسمت، سه مختصات مهم کارتزین، استوانه ای، کروی را بررسی میکنیم . در هر کدام از این مختصات ها 3 المان طولی ،سطحی و حجمی را بیان میکنیم که متناسب با مسائل باید ابتدا دستگاه مختصات را به درستی انتخاب کنید و سپس المان خود را انتخاب کنید.
مختصات دکارتی یا کارتزین:
متغیرهای این دستگاه مختصات که با آن میتوان هر نقطهی دلخواه از فضا را با آن توصیف کرد، با (x,y,z) نشان داده میشود.
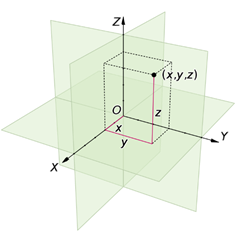
المان طولی(مسیر): برای مسائلی که توزیع خطی دارد، مانند میله باردار مستقیم.
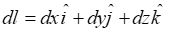
المان سطحی: برای مسائل توزیع سطحی، مانند سطوح یک مکعب یا مکعب مستطیل و سطوح مشابه.
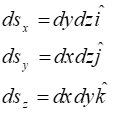
المان حجمی: برای حجم یک مکعب یا مکعب مستطیل.
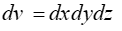
مختصات استوانهای:
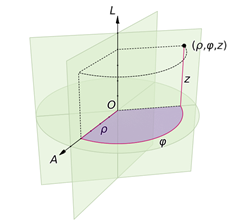
متغیرهای دستگاه مختصات استوانهای که با آن میتوان هر نقطهی دلخواه از فضا را با آن توصیف کرد با (r,θ,z) نشان داده می شود. در برخی منابع متغیر ها را با (ρ,φ,z) نشان میدهند که هیچ تفاوتی ندارد.
نکته: دستگاه مختصات قطبی حالت خاص از دستگاه استوانهای است، زمانی که بدنه استوانه را حذف نماییم. در این حالت متغیرهای فضایی به صورت (r,θ) درمیآیند.
- المان طولی(مسیر): برای مسائلی که توزیع خطی دارد مانند میله باردار قوسدار یا حلقه جریان و بار.
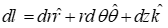
- المان سطحی: برای مسائل توزیع سطحی مانند یک دیسک (سطوح بالا و پایین استوانه) و پوسته استوانهای با بار الکتریکی یا جریان(سطح جانبی یا بدنه استوانه).
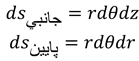
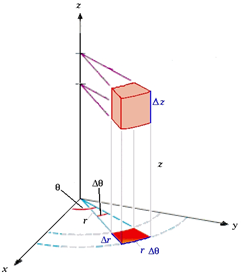
- المان حجمی: برای حجم یک استوانهی توپر یا قاچی از یک استوانه.
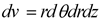
مختصات کروی:
متغیرهای دستگاه مختصات کروی که با آن میتوان هر نقطه دلخواه از فضا را با آن توصیف کرد با (r,θ,φ) نشان داده میشود.
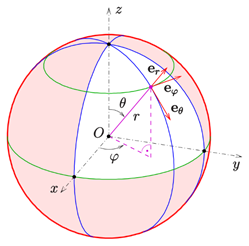
- المان طولی(مسیر): برای مسائلی که توزیع خطی دارد (بسیار کم کاربرد!).
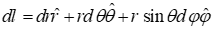
- المان سطحی: برای مسائل توزیع سطحی مانند پوسته کروی یا پوسته نیمکره.
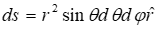
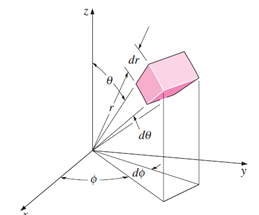
- المان حجمی: برای یک کره توپر یا یک نیمکره توپر.
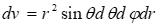
گاهاً در برخی از مسائل ممکن است نیاز به تبدیلات از مختصات کروی به دکارتی یا بالعکس باشد. این کار توسط تبدیلات زیر انجام میشود.
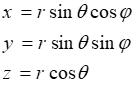
مشتقهای کاربردی درفیزیک 2 (سعی کنید این مشتق ها را به خاطر بسپارید)
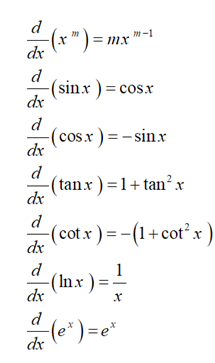
مشتق توابع کسری به صورت ذیل است:
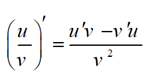
انتگرالهای کاربردی درفیزیک 2

انتگرالهای چندگانه:
برای محاسبه مساحت انتگرال دوگانه لازم است و برای محاسبه یا جاروب حجم، انتگرال سهگانه. اما آنچه در این درس اهمیت دارد آن است که میتوان در هر دو صورت انتگرالهای چندگانه را به صورت ضرب ساده چند انتگرال یگانه نوشت.
انتگرال دوگانه:
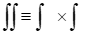
انتگرال سهگانه:
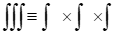
برای آموزش بهتر این مبحث پیشنهاد ما این است که بخش ابتداییدورهی فیزیک۲ لینوم رو مشاهده کنین یا میتوانین برای تسلط بیشتر بر این مباحث ریاضی ۱ ما رو هم مشاهده کنین.