قانون های نیوتون
مکانیک نیوتونی
در این مقاله به مطالعه سه قانون بنیادی نیوتون دربازهحرکت می پردازیم. مکانیک نیوتونی در همه حالت ها به کار نمی رود. اگر تندی اجسام بر هم کنش کننده خیلی زیاد- درحد کسربزرگی از تندی نور- باشد، به جای مکانیک نیوتونی باید از نظریه نسبیت خاص اینشتین استفاده کرد، که درباره هر تندی ای از جمله تندی های نزدیک به تندی نور، صادق است.
اگر اجسام برهم کنش کننده در حد مقیاس ساختار اتمی( مثلا الکترون های درون اتم) باشند، باید مکانیک نیوتونی را با مکانیک کوانتومی جانشین کرد. امروزه، فیزیک دانان به مکانیک نیوتونی به صورت حالت خاصی از این دو نظریه جامع تر نگاه می کنند.
مکانیک نیوتونی در موردحرکت گسترده وسیعی از اجسام از اندازه های بسیار کوچک ( تقریبا در مقیاس ساختار اتمی) تا اندازه های نجومی ( اشیایی ماند کهکشان و خوشه های کهکشانی ) به کار می رود.
قانون اول نیوتون
اگر یک قرص هاکی را روی یک کف پوش چوبی بلغزانیم، در عمل سرعتش کم و سپس متوقف می شود. اگر بخواهیم آن را با سرعت ثابت به حرکت در آوریم باید به طور پیوسته آن را بکشیم یا هل بدهیم. حال اگر همین قرص را روی سطح یخ بسته ی کیدان بازی ایکیت به حرکت در آوریم، مسافت بیشتری می پیماید.
اکنون می توانیم سطح های لغزنده تر و طولانی تر را در نظر بگیریم که قرص بتواند تا مسافت بیشتری روی آن بلغزد. در نهایت سطح بسیار لغزنده و درازی ( که سطح بی اصطکاک نامیده می شود) می توان تصور کرد که سرعت قرص روی آن به سختی کاهش پیدا کند.
از این مشاهدات می توان نتیجه گرفت که یک جسم به شرطی با سرعت ثابت حرکت می کند که هیچ نیرویی به آن وارد نشود. این نتیجه ما را به قانون اول از سه قانون نیوتون درباره حرکت رهنمون می شود:
قانون اول نیوتون به نحوی مناسب تر و بر حسب نیروی خالص چنین بیان می شود:
قانون اول نیوتون: هرگاه به جسمی هیچ نیروی خالصی وارد نشود (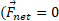 ، سرعت جسم نمی تواند تغیر کند؛ یعنی جسم نمی تواند شتاب داشته باشد.
، سرعت جسم نمی تواند تغیر کند؛ یعنی جسم نمی تواند شتاب داشته باشد.
یک جسم ممکن است تحت اثر چند نیرو قرار گیرد، اما اگر نیروی خالص ( نیروی برآیند) آن ها صفر باشد جسم شتاب ندارد. بنابراین اگر به طور تصادفی دریابیم که سرعت جسمی ثابت است، بی درنگ می توان گفت که نیروی وارد شده به آن صفر است.
قانون دوم نیوتون
نیروی برایند وارد شده به یک جسم برابر با حاصل ضرب جرم جسم در شتاب آن استت.
این گزاره را از لحاظ فرمولی می توان به شکل زیر ارائه داد
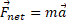
جسم را معین کنید. نخست باید بدانیم که آن را درباره چه جسمی به کار می بریم. سپس،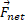 باید مجموع برداری تمام نیروهای وارد شده به آن جسم باشد. فقط نیروهایی را که به آن جسم اثر می کنند، در مجموع برداری در نظر می گیریم، نه نیروهایی که در حالت معینی باید به اجسام دیگر وارد شوند.
باید مجموع برداری تمام نیروهای وارد شده به آن جسم باشد. فقط نیروهایی را که به آن جسم اثر می کنند، در مجموع برداری در نظر می گیریم، نه نیروهایی که در حالت معینی باید به اجسام دیگر وارد شوند.
محورها را جدا کنید. معادله بالا با سه معادله مولفه ای زیر هم ارز است، که هر کدام برای یکی از محورهای دستگاه مختصات 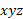 نوشته می شوند:
نوشته می شوند:
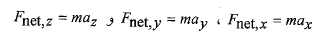
هر یک از این معادله ها مولفه نیروی برایند در روی یک محور مختصات را به شتاب در راستای آن محور ربط می دهد. مولفه شتاب در راستای یک محور معین فقط توسط مجموع مولفه های نیرو در راستای همان محور تولید می شود و مولفه های نیرو در راستای محورهای دیگر بر این شتاب اثری ندارند.
قانون اول نیوتون: هرگاه به جسمی هیچ نیرویی وارد نشود، سرعت جسم نمی تواند تغییر کند؛ یعنی، جسم نمی تواند شتاب داشته باشد.
به عبارت دیگر اگر جسم در حال سکون باشد، به حال سکون باقی می ماند و اگر در حال حرکت باشد، با همان سرعتی که دارد (از لحاظ بزرگی و جهت) به حرکت ادامه می دهد.
تعادل نیروها. معادله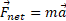 نشان میدهد که اگر نیروی برایند وارد شده به جسمی صفر باشد، شتاب جسم صفر است. در این صورت جسم اگر در حال سکون باشد، به حال سکون می ماند و اگر در حال حرکت باشد با سرعت ثابت به حرکتش ادامه می دهد. در چنین حالت هایی، نیروهای وارد شده به جسم با یکدیگر متوازن می شوند، می توان گفت نیروها و جسم در حال تعادل اند. در این حالت گفته می شود که نیروها اثر یکدیگر را حذف می کنند.
نشان میدهد که اگر نیروی برایند وارد شده به جسمی صفر باشد، شتاب جسم صفر است. در این صورت جسم اگر در حال سکون باشد، به حال سکون می ماند و اگر در حال حرکت باشد با سرعت ثابت به حرکتش ادامه می دهد. در چنین حالت هایی، نیروهای وارد شده به جسم با یکدیگر متوازن می شوند، می توان گفت نیروها و جسم در حال تعادل اند. در این حالت گفته می شود که نیروها اثر یکدیگر را حذف می کنند.
یکاها. با استفاده کردن از معادله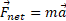 برای یکاهای
برای یکاهای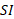 می توان نوشت
می توان نوشت
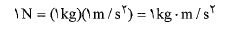
نمودارها. برای حل کردن مسئله ها با به کاربردن قانون دوم نیوتون اغلب مناسب تر است که یک نمودار جسم-آزاد رسم کنیم و تنها جسمی را نشان دهیم که می خواهیم برایند نیروهای وارد شده به آن را در نظر بگیریم.
فقط نیروهای خارجی. یک دستگاه شامل یک یا چند جسم است وهر نیرو که از سوی اجسام خارج دستگاه به اجسام درون دستگاه وارد شود، نیروی خارجی نام دارد. اگر اجسام به سختی به هم متصل شد باشند، دستگاه را به صورت یک جسم مرکب هم می توان در نظر گرفت و نیروی برایند 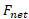 که به آن داده می شود، مجموع برداری تمام نیروهای خارجی است. می توانیم نیروی خارجی برایند وارد شده به یک دستگاه را از طریق قانون دوم نیوتون
که به آن داده می شود، مجموع برداری تمام نیروهای خارجی است. می توانیم نیروی خارجی برایند وارد شده به یک دستگاه را از طریق قانون دوم نیوتون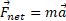 به شتاب آن دستگاه ربط دهیم که در آن
به شتاب آن دستگاه ربط دهیم که در آن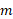 جرم کل دستگاه است.
جرم کل دستگاه است.
 مسئله نمونه- نیروهای دوبُعدی، قوطی آب نبات
مسئله نمونه- نیروهای دوبُعدی، قوطی آب نبات
در اینجا با استفاده کردن از شتاب نیروی نامعلوم را به دست می آوریم
قسمت الف شکل زیر نمای یک قوطی آب نبات 2 کیلوگرمی را با دید از بالا نشان می دهد، که روی یک سطح افقی بی اصطکاک با شتاب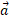 به بزرگی
به بزرگی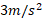 در جهت نشان داده شده در شکل حرکت می کند. این شتاب توسط سه نیروی واقع در صفحه افقی ایجاد می شود که دوتای آن ها نشان داده شده اند:
در جهت نشان داده شده در شکل حرکت می کند. این شتاب توسط سه نیروی واقع در صفحه افقی ایجاد می شود که دوتای آن ها نشان داده شده اند: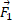 دارای بزرگی
دارای بزرگی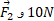 دارای بزرگی
دارای بزرگی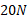 است. نیروی سوم
است. نیروی سوم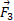 با استفاده کردن از نمادگذاری بردارهای یکه و به صورت بزرگی – زاویه، چیست؟
با استفاده کردن از نمادگذاری بردارهای یکه و به صورت بزرگی – زاویه، چیست؟
نیروی برایند وارد شده به قوطی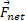 برابر با مجموع برداری سه نیرو است و رابطه آن با شتاب
برابر با مجموع برداری سه نیرو است و رابطه آن با شتاب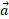 بر پایه قانون دوم نیوتون
بر پایه قانون دوم نیوتون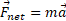 است. پس می توان نوشت
است. پس می توان نوشت
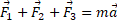
و از آنجا داریم
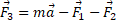
حل: چون این مسئله یک مسئله دو بُعدی است، فقط با قرار دادن بزرگی کمیت های برداری طرف راست معادله
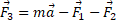 نمی توان
نمی توان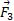 را پیدا کرد. بلکه باید
را پیدا کرد. بلکه باید 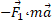 ( ناهمسو با
( ناهمسو با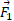 ) و
) و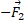 (ناهمسو با
(ناهمسو با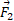 ) در شکل زیر قسمت ب را به طور برداری با هم جمع کرد.
) در شکل زیر قسمت ب را به طور برداری با هم جمع کرد.
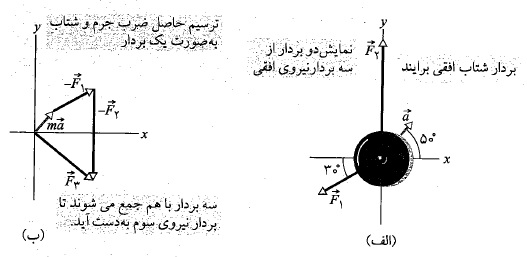
این عمل جمع را با استفاده کردن از ماشین ویژه محاسبه های بردازی نیز می توان انجام داد، زیرا بزرگی و زاویه هر سه بردار در دست است. اکنون طرف راست معادله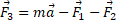 را بر حسب مولفه ها، نخست در راستای محور
را بر حسب مولفه ها، نخست در راستای محور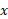 و سپس در راستای محور
و سپس در راستای محور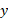 حساب می کنیم. ( در یک زمان فقط از یک محور استفاده کنید.)
حساب می کنیم. ( در یک زمان فقط از یک محور استفاده کنید.)
مولفه های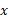 : برای مولفه های محور
: برای مولفه های محور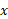 داریم
داریم

پس از جانشانی داده های معلوم داریم
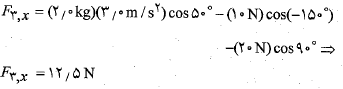
مولفه های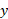 : به همین ترتیب در راستای محور
: به همین ترتیب در راستای محور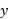 داریم
داریم
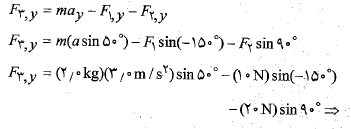
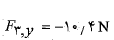
بردار: با استفاده کردن از نمادگذاری بردارهای یکه داریم
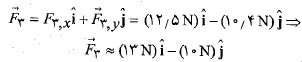
اکنون با استفاده کردن از ماشین ویژه محاسبه های برداری می توان بزرگی و زاویه بردار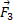 را معین کرد. هم چنین برای بدست آوردن بزرگی و زاویه ( نسبت به محور
را معین کرد. هم چنین برای بدست آوردن بزرگی و زاویه ( نسبت به محور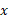 مثبت) داریم
مثبت) داریم
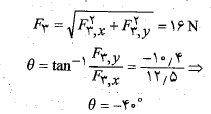
قانون سوم نیوتون
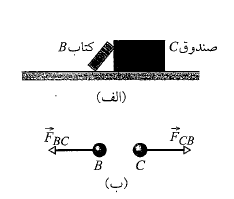
وقتی دو جسم یکدیگر را می کشند یا هل می دهند، یعنی وقتی یک جسم نیرویی به جسم نیرویی به جسم دیگر وارد می کند، گفته می شود که دو جسم بر هم کنش دارند. برای مثال، فرض کنید کتاب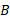 را به صندوق
را به صندوق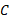 تکیه می دهیم ( قسمت الف شکل). در این صورت کتاب و صندوق بر هم کنش دارند؛ یعنی در اینجا یک نیروی افقی
تکیه می دهیم ( قسمت الف شکل). در این صورت کتاب و صندوق بر هم کنش دارند؛ یعنی در اینجا یک نیروی افقی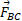 وارد شده به کتاب از سوی صندوق ( یا ناشی از صندوق) و یک نیروی افقی
وارد شده به کتاب از سوی صندوق ( یا ناشی از صندوق) و یک نیروی افقی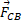 وارد شده به صندوق از سوی کتاب ( یا ناشی از کتاب ) وجود دارد. این زوج نیرو در قسمت ب شکل نشان داده شده است.
وارد شده به صندوق از سوی کتاب ( یا ناشی از کتاب ) وجود دارد. این زوج نیرو در قسمت ب شکل نشان داده شده است.
قانون سوم نیوتون: هرگاه دو جسم بر هم کنش داشته باشند نیروهای وارد شده به هر یک از آن دو ازسوی جسم دیگر همیشه ازلحاظ بزرگی مساوی و از لحاظ جهت مخالف یکدیگرند.
برای کتاب وصندوق بیان فرمولی این قانون می تواند با رابطه نرده ای زیر

یا با رابطه برداری زیر نوشته شود

در اینجا علامت منفی نشان می دهد که این دو نیرو از لحاظ جهت مخالف یکدیگرند. نیروهای میان دو جسم برهم کنش کننده را می توان زوج نیروهای قانون سوم نامید. وقتی دو جسم به هر حالتی برهم کنش داشته باشند یک زوج نیروی قانونسوم به وجود می آید. در شکل قسمت الف، کتاب و صندوق ساکن اند، اما اگر آن هاحرکتکنند یا حتی دارای حرکت شتاب دار باشند، قانون سوم با زهم درباره آن ها صادق است.
کاربرد قانون های نیوتون
در اینجا موضوع مهم برگرداندن یک شکل طرح وار فیزیکی به نمودار جسم – آزاد با محورهای مناسب است تا بتوان از قانون های نیوتون استفاده کرد.
 مسئله نمونه جسم روی میز، جسم آویخته
مسئله نمونه جسم روی میز، جسم آویخته
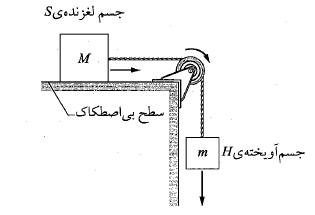
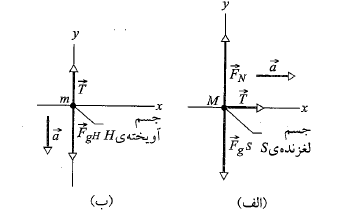
شکل زیر جسم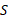 ( جسم لغزنده) به جرم
( جسم لغزنده) به جرم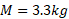 را نشان می دهد. این جسم می تواند بر روی یک سطح افقی بی اصطکاک، آزادانه حرکت کند و به وسیله ریسمانی که از روی قرقره ی بی اصطکاکی عبور کرده، به جسم
را نشان می دهد. این جسم می تواند بر روی یک سطح افقی بی اصطکاک، آزادانه حرکت کند و به وسیله ریسمانی که از روی قرقره ی بی اصطکاکی عبور کرده، به جسم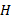 ( جسم آویخته) به جرم
( جسم آویخته) به جرم
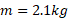 وصل شده است. ریسمان و قرقره در مقایسه با جرم اجسام دارای جرم ناچیز ( یعنی، «بی جرم») هستند. هنگامی که جسم آویخته
وصل شده است. ریسمان و قرقره در مقایسه با جرم اجسام دارای جرم ناچیز ( یعنی، «بی جرم») هستند. هنگامی که جسم آویخته 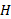 سقوط می کند، جسم لغزنده
سقوط می کند، جسم لغزنده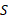 به سمت راست شتاب پیدا می کند. مطلوب است تعیین (الف) شتاب جسم لغزنده
به سمت راست شتاب پیدا می کند. مطلوب است تعیین (الف) شتاب جسم لغزنده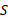
(ب) شتاب جس آویخته 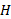 و (پ) نیروی کشش ریسمان
و (پ) نیروی کشش ریسمان
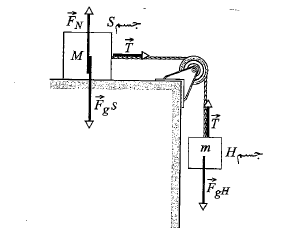
حل: مطابق شکل زیر پنج نیرو به اجسام اثر می کنند:
فرض می کنیم که ریسمان کش نمی آید در نتیجه اگر جسم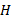 در یک مدت معین به اندازه یک میلیمتر سقوط کند جسم
در یک مدت معین به اندازه یک میلیمتر سقوط کند جسم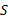 در همان مدت به اندازه یک میلیمتر به سمت راست حرکت می کند. در نتیجهه با هم حرکت می کنند و شتاب آن ها دارای بزرگی یکسان
در همان مدت به اندازه یک میلیمتر به سمت راست حرکت می کند. در نتیجهه با هم حرکت می کنند و شتاب آن ها دارای بزرگی یکسان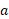 است.
است.
نیروها، جرم ها و شتاب ها در مسئله دخالت دارند و باید از قانون دوم نیوتون درباره حرکت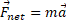 استفاده کرد. قرقره را نادیده می گیریم زیرا فرض می کنیم جرم آن درمقایسه با جرم دو جسم قابل چشم پوشی است. کار قرقره فقط سمت گیری ریسمان است.
استفاده کرد. قرقره را نادیده می گیریم زیرا فرض می کنیم جرم آن درمقایسه با جرم دو جسم قابل چشم پوشی است. کار قرقره فقط سمت گیری ریسمان است.
ابتدا جسم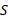 را به صورت ذره ای به جرم
را به صورت ذره ای به جرم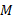 نمایش می دهیم و تمام نیروهای وارد شده به آن را مطابق شکل زیر قسمت الف، رسم می کنیم. آنچه به دست می آید نمودار جسم-آزاد مربوط به جسم است. سپس دستگاه محورهای مختصات را رسم می کنیم. بهتر است محور
نمایش می دهیم و تمام نیروهای وارد شده به آن را مطابق شکل زیر قسمت الف، رسم می کنیم. آنچه به دست می آید نمودار جسم-آزاد مربوط به جسم است. سپس دستگاه محورهای مختصات را رسم می کنیم. بهتر است محور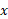 را به موازات سطح میز و در جهتحرکت جسم لغزنده انتخاب کنبم.
را به موازات سطح میز و در جهتحرکت جسم لغزنده انتخاب کنبم.
رابطه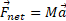 یک معادله برداری است پس می توان آن را به صورت سه معادله مولفه ای زیر نوشت:
یک معادله برداری است پس می توان آن را به صورت سه معادله مولفه ای زیر نوشت:
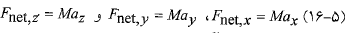
که در آن 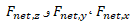 مولفه های نیروی برایند در راستای سه محوراند. اکنون می توانیم هر معادله مولفه ای را برای راستای مربوط بنویسیم. چون جسم
مولفه های نیروی برایند در راستای سه محوراند. اکنون می توانیم هر معادله مولفه ای را برای راستای مربوط بنویسیم. چون جسم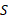 در راستای قائم شتاب ندارد معادله
در راستای قائم شتاب ندارد معادله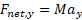 چنین نوشته می شود
چنین نوشته می شود
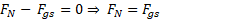
بنابراین در راستای محور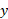 ، بزرگی نیروی عمودی با بزرگی نیروی گرانشی برابر است. در راستای محور
، بزرگی نیروی عمودی با بزرگی نیروی گرانشی برابر است. در راستای محور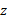 که بر صفحه کتاب عمود است، هیچ نیرویی اثر نمی کند. در راستای محور
که بر صفحه کتاب عمود است، هیچ نیرویی اثر نمی کند. در راستای محور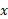 فقط مولفه نیرو وجود دارد که همان
فقط مولفه نیرو وجود دارد که همان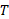 است. پس معادله
است. پس معادله 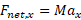 را می توان چنین نوشت
را می توان چنین نوشت
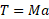
این معادله شامل دو کمیت نامعلوم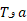 است و نمی توان آن را حل کرد.
است و نمی توان آن را حل کرد.
کاربرد رابطه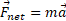 همان است که در مورد جسم
همان است که در مورد جسم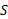 انجام شد: نمودار جسم- آزاد مربوط به جسم
انجام شد: نمودار جسم- آزاد مربوط به جسم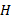 را مطابق قسمت ب شکل بالا رسم می کنیم و سپس معادله
را مطابق قسمت ب شکل بالا رسم می کنیم و سپس معادله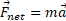 را به صورت مولفه ای به کار می بریم. در اینجا چون شتاب در راستای محور
را به صورت مولفه ای به کار می بریم. در اینجا چون شتاب در راستای محور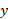 است، از معادله
است، از معادله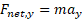 استفاده می کنیم و چنین می نویسیم
استفاده می کنیم و چنین می نویسیم
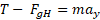
اکنون می توان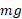 را به جای
را به جای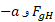 را به جای
را به جای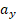 ( علامت منفی به خاطر حرکت کردن جسم
( علامت منفی به خاطر حرکت کردن جسم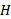 در جهت منفی محور
در جهت منفی محور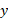 است) قرار داد. درنتیجه داریم
است) قرار داد. درنتیجه داریم
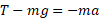
سپس معادله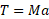 و
و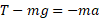 را از هم کم می کنیم در نتیجه داریم
را از هم کم می کنیم در نتیجه داریم
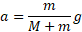
با جانشانی این نتیجه در معادله 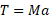 داریم
داریم
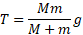
با قرار دادن مقادیر عددی معلوم در معادله های بالا خواهیم داشت
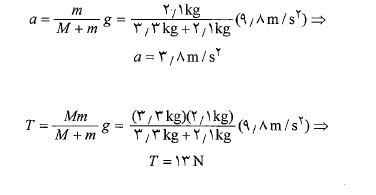
برای مطالعه مباحث پیشرفته از محصول دورهآموزشی فیزیک عمومی1 از سایت لینوم استفاده کنید.