حرکت نسبی یک بُعدی  و دو بُعدی

فرض کنید مرغابی ای را میبینید که با سرعت 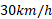  به سمت شمال پرواز می کند. از نظر مرغابی دیگری که در کنار آن مرغابی در حال پرواز کردن است، مرغابی اول ساکن به نظر می رسد. به عبارت دیگر سرعت یک ذره به چارچوب مرجع عنصر در حال مشاهده یا در حال اندازه گیری سرعت ذره بستگی دارد.

برای منظوری که ما داریم چارچوب مرجع یک شی فیزیکی  است که دستگاه مختصات را به آن متصل می کنیم. در زندگی روزانه این شیء زمین است. برای مثال تندی های نوشته شده در برگ فهرست تندی های مجاز رانندگی، همیشه نسبت به زمین اندازه گیری می شوند. اما تندی نسبت به افسر پلیس که در حال حرکت کردن با خودرو خود آن را اندازه می گیرد متفاوت است.

فرض کنید امیر ( واقع در مبداء چارچوب مرجع 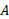  در شکل زیر) که خودرو خود را در کنار بزرگ راهی متوقف کرده است، خودرو در حال عبور 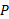(ذره) را مشاهده می کند.

 بهروز ( واقع در مبداء چارچوب مرجع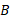 ) که با تندی ثابت در بزگ راه در حال رانندگی است نیز خودرو 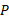 را مشاهده می کند.  فرض کنید هر دو ناظر در لحظه معینی در صدد تعیین مکان خودرو 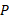 هستند. با توجه به شکل داریم

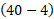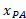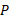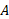معادله  چنینن خوانده می شود:« ، مختصه اندازه گیری شده خودرو  توسط  برابر است با 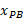، مختصه اندازه گیری شده خودرو 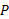 توسط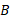 ، به علاوه 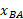، مختصه اندازه گیری شده 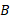 توسط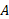 ». به ترتیب شاخص های پایین در موقع خواندن جمله های معادله بالا توجه کنید. با مشتق گرفتن از معادله 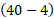 نسبت به زمان، داریم

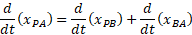
بنابراین رابطه مولفه های سرعت عبارت از

معادله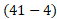 را به این صورت می خوانیم:« 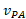، سرعت اندازه گیری شده خودرو 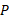 توسط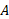  برابر است با 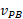 ، سرعت اندازه گیری شده خودرو 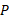 توسط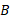  ، به علاوه 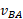 ، سرعت اندازه گیری شده 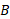 توسط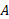 ». جمله 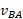 سرعت چارچوب 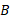 نسبت به چارچوب 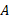 است.

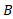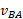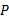در اینجا فقط چارچوب های مرجعی را در نظر می گیریم که نسبت به هم با سرعت ثابت حرکت می کنند. در مثالی که ارائه شد موضوع چنین است که بهروز ( چارچوب ) همیشه با سرعت ثابت  نسبت به امیر (چارچوب )حرکت می کند. اما خودرو  ( ذره در حال حرکت) ممکن است سرعتش زیاد یا کم شود، یا متوقف گردد یا جهش وارون شود ( به هر حال خودرو 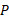 می تواند شتاب دار باشد).

برای تعیین رابطه شتاب خودرو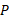  که توسط بهروز و امیر اندازه گیری می شود از معادله  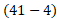نسبت به زمان مشتق می گیریم، داریم

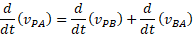
چون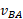  ثابت است، جمله آخر سمت راست معادله صفر است. در نتیجه داریم

به عبارت دیگر:

ناظرهای واقع در چارچوب های مرجع مختلف ( که نسبت به هم با سرعت ثابتی حرکت می کنند)، برای یک ذره در حالحرکت شتاب یکسانی را اندازه می گیرند.

مسئله نمونه: حرکت نسبی یک بُعدی امیر و بهروز

در شکل بالا فرض کنید سرعت بهروز نسبت به امیر ثابت و برابر با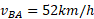  است و خودرو 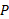 در جهت منفی محور 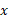 می کند.

الف) اگر سرعت خودرو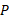  نسبت به امیر مقدار ثابت 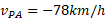 باشد، سرعت خودرو 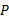 نسبت به بهروز 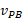 چیست؟

حل : داریم

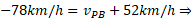
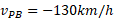
اگر خودرو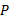  به وسیله یک طناب پیچیده شده به دور قرقره به خودرو بهروز وصل می شد، هنگام دور شدن دو خودرو از هم طناب با تندی 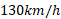 از قرقره باز می شد.

ب) اگر خودرو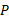  با شتاب ثابت ترمز کند و پس از زمان 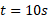 نسبت به امیر ( و در نتیجه نسبت به زمین) متوقف شود، شتاب 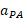 نسبت به امیر چقدر است؟

حل: سرعت آغازی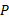  نسبت به  امیر 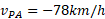 و سرعت پایانی صفر است. بنابراین شتاب نسبت به امیر برابر است با

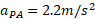
پ)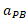 شتاب خودرو 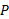 نسبت به بهروز درحین ترمز کرد چیست؟

حل: سرعت آغازی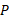  نسبت به بهروز با توجه به قسمت (الف) در دست است( 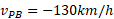) ، سرعت پایانی 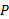 نسبت به بهروز 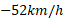 است ( این مقدار سرعت خودرو متوقف شده نسبت به بهروز در حال حرکت است). بنابراین داریم

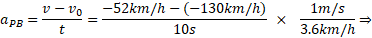
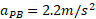
این همان نتیجه ای است که از پیش می دانستیم: چون امیر و بهروز دارای سرعت نسبی ثابت اند، برای خودرو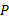  شتاب یکسانی را اندازه می گیرند.

حرکت نسبی دو بُعدی

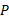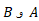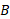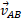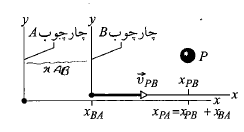
دو ناظر مورد نظر ما باز هم خودرو  را از مبداء چارچوب های مرجع   در حالی که  با سرعت ثابت  نسبت به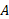  حرکت می کند ( محورهای متناظر این دو چارچوب موازی اند)، مشاهده می کنند و شکل زیر لحظه معینی از حرکت را نشان می دهد.

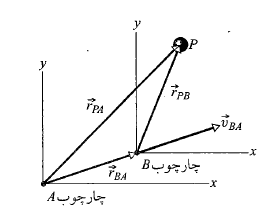
در آن لحظه، بردار مکان مبداء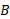  نسبت به مبداء 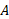، به صورت 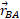 است. هم چنین بردارهای مکان ذره 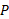 عبارت اند از 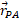  نسبت به مبداء 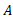 و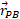   نسبت به مبداء 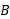. با توجه به وضعیت سَرها و دُم های این سه بردار مکان در شکل، می توان نوشت

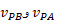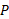با مشتق گرفتن از این معادله نسبت به زمان می توان رابطه میان سرعت های   ذره  نسبت به ناظرهای  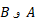 را به دست آورد:

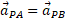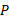اگر از این رابطه نسبت به زمانمشتق بگیریم، شتاب های  ذره  نسبت به ناظرها به دستمی آیند. اما توجه کنید که چون 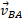 ثابت است، مشتق آن نسبت به زمان صفر است. بنابراین داریم

در اینجا نیز مانند حرکت یک بُعدی این قاعده استنتاج می شود: ناظرهای واقع در چارچوب های مرجع مختلف که نسبت به هم با سرعت ثابتی حرکت می کنند، برای ذره در حال حرکت یک شتاب یکسان را اندازه می گیرند.

مسئله نمونه : حرکت نسبی دو بُعدی هواپیماها

قسمت الف شکل زیر نشان می دهد که هواپیمایی قرار است به سمت خاور پرواز کند. اما چون بادی به سمت شمال و متمایل به خاور می وزد، خلبان مجبور است که هواپیما را نسبت به محور خاوری اندکی به سمت جنوب هدایت کند. سرعت هواپیما نسبت به باد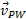  ، بزرگی آن 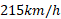 و زاویه آن نسبت به محور خاوری و متمایل به جنوب 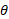 است. سرعت باد نسبت به زمین 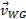، بزرگی آن 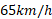 و زاویه آن نسبت به محور شمالی و متمایل به خاور 20 درجه است. زاویه 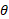 و بزرگی سرعت هواپیما نسبت به زمین 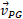 چیست؟

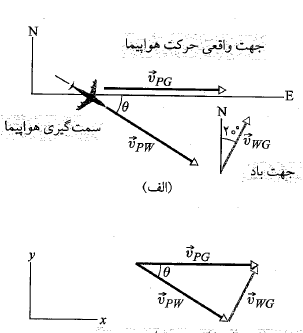
حل: نخست رابطه زیر را برای سه بردار نشان داده شده در قسمت ب شکل بالا می نویسیم

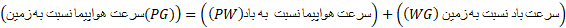
این رابطه را می توان به صورت برداری زیر نوشت

بهتر آن است که بردارها را به مولفه های آن ها در دستگاه مختصات قسمت (ب) شکل بالا تجزیه وسپس معادله (4-46) را برای هریک از محورها حل کنیم. برای مولفه های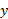  داریم

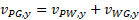
یا

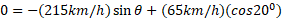
پس از حل کردن این معادله نسبت به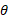  داریم

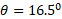
به همین ترتیب برای مولفه های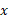  داریم

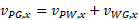
در اینجا چون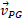  با محور 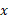 موازی است، مولفه  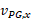 با بزرگی 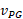 برابر است. با جانشانی این مقدار و به ازای 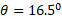 داریم

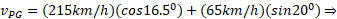
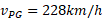
حرکت دایره ای یکنواخت

وقتی جسمی با تندی ثابت  در یک مسیر دایره ای حرکت می کند، می گوییم حرکت دایره ای یکنواخت انجام می دهد. در این حرکت جسم دارای یک شتاب مرکزگرا ( به سوی مرکز دایره) با بزرگی ثابت زیر است

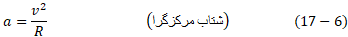
که در آن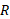  شعاع دایره است.

نیرو مرکزگرا با تغییر دادن جهت سرعت جسم بدون تغییر دادن تندی، به جسم شتاب می دهد. با استفاده کردن از قانون دوم نیوتون و معادله (6-17) (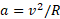 ) ، بزرگی 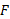، نیروی مرکزگرا ( یایک نیروی مرکزگرای برآیند) را می توان از معادله ی زیر به دست آورد

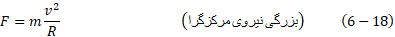
چون در اینجا تندی  ثابت است، بزرگی های شتاب و نیرو هم ثابت اند. اما جهت های شتاب و نیروی مرکزگرا ثابت نیستند و پیوسته تغییر می کنند،  به گونه ای که همیشه به سوی مرکز دایره اند.به همین دلیل بردارهای نیرو و شتاب را گاهی در راستای محور شعاعی که همراه جسم حرکت می کند، رسم می کنند. این محور همیشه از مرکز دایره به سوی جسم، مطابق شکل کشیده می شود. جهت مثبت محور شعاعی به برون سوی دایره است، اما بردارهای شتاب و نیرو در راستای شعاع و به درون سوی دایره اند.

مسئله نمونه- حلقه دایره ای قائم، دیاوُلو

اغلب به خاطر سوار شدن خودرو به حرکت دایره ای افقی عادت کرده ایم. اما حرکت دایره ای قائم می تواند تازگی داشته باشد. در یک سیرک آلو دیاولو سوار بر دوچرخه در یک مسیر حلقه ای قائم مانند قسمت الف شکل زیر به اجرای نمایش پرداخت. فرض کنید حلقه به صورت دایره ای به شعاع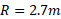  باشد. کمترین تندی ، که دیالوو و دوچرخه اش باید داشته باشند تا بتوانند در بالای حلقه در تماس با مسیر باقی بمانند چقدر است؟

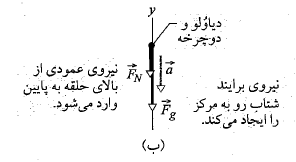
نمودار جسم -آزاد قسمت ب شکل زیر نیروهایی را که در بالاترین نقطه حلقه به ذره وارد می شوند، نشان می دهد. نیروی گرانشی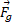 در راستای محور 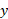 به پایین سو و نیروی عمودی 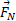 که حلقه به ذره وارد می کند، نیز به پایین سو است. بنابراین با استفاده کردن از قانون دوم نیوتون برای مولفه های مربوط به محور 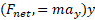 داریم

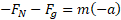
یا

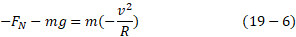
اگر ذره کمترین تندی  را برای باقی ماندن روی حلقه داشته باشد، در آستانه جدا شدن از حلقه خواهد بود، که به معنی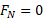  است. باجانشانی این مقدار 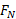 در معادله 6-19 حل کردن معادله نسبت به  و جانشانی مقادیر معلوم داریم

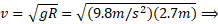
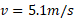
مسئله نمونه – خودرو در یک پیچ دایره ای تخت

قسمت الف شکل زیر یک خودرو مسابقه جایزه بزرگ به جرم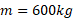  را نشان می دهد که در یک مسیر دایره ای تخت به شعاع 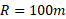 حرکت می کند. به خاطر شکل خودرو و بال های نصب شده بر روی آن، هوای در حال گذر از پیرامون یک نیروی پایی سوی برآر منفی 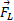 ، به خودرو وارد می کند. ضریب اصطکاک ایستایی میان لاستیک ها و مسیر 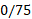 است. ( فرض کنید نیروهای وارد شده به هریک از چهار لاستیک برابراند). (الف) اگر خودرو در حال حرکت کردن با تندی 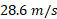 در آستانه بیرون لغزیدن از پیچ باشد، بزرگی نیروی برآر منفی 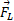 پایین سوی وارد شده به خودرو چقدر است؟

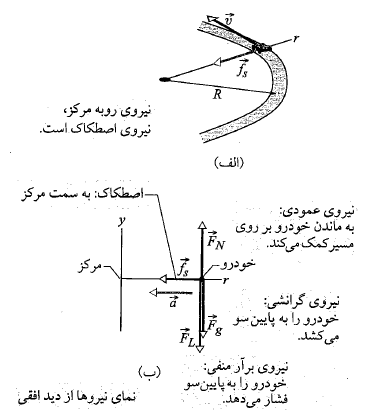
محاسبات راستای شعاعی: در نمودار جسم- آزاد قسمت ب شکل فوق نیروی اصطکاک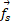   نشان داده شده است. این نیرو د رجهت منفی محور شعاعی  است که همیشه از مرکز خمیدگی تا محل خودرو در حال حرکت ادامه دارد. این نیرو یک شتاب مرکزگرا با بزرگی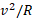  به وجود می آورد. با نوشتن قانون دوم نیوتون برای مولفه های واقع در راستای محور  می توان رابطه میان این نیرو و شتاب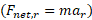  را چنین نوشت

با قرار دادن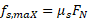  به جای 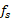 در این رابطه داریم

محاسبات راستای قائم: اکنون نیروهای قائم وارد شده به خودرو را در نظر بگیرید. در قسمت ب شکل جهت نیروی عمودی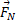  به سمت بالا و در جهت مثبت محور 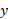 است. جهت نیروی گرانشی 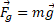 و جهت نیروی برآر منفی 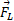 به سمت پایین است. شتاب خودرو در راستای محور 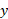 صفر است. بنابراین قانون دوم نیوتون برای مولفه های مربوط به راستای محور 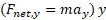 می توان چنین نوشت

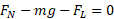
یا

ترکیب کردن نتیجه ها: اکنون مقدار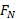  از معادله 6-22 را در معادله 6-21 قرار م یدهیم تا نتیجه های بدست آمده برای راستاهای دومحور با هم ترکیب شوند. با انجام دادن این کار و سپس حل کردن معادله حاصل نسبت به 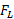 داریم

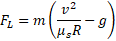
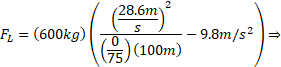
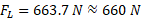
ب)بزرگی نیروی برآر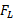  وارد شده به خودرو درست مانند نیروی پسار به مجذور تندی 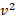 بستگی دارد. بنابراین خودرو وقتی تندترحرکت می کند درست مانند وقتی که در بخش مستقیم جاده حرکت می کند نیروی برآر منفی وارد شده به آن بیشتر می شود. بزرگی نیروی برآور منفی برای تندی 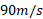 چقدر است؟ 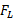 با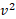  متناسب است.

حل: بدین ترتیب نسبت نیروی برآر منفی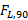  در تندی 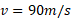 به نیروی برآر منفی 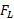 در تندی 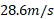را چنین می توان نوشت

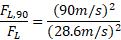
با جانشانی نیروی برآر منفی معلوم 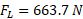  ، مقدار 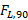 چنین به دست می آید

برای مطالعه مباحث پیشرفته از محصولدوره آموزشی فیزیک عمومی 1 در سایت لینوماستفاده کنید.