مرکز جرم و تکانه خطی

مرکز جرم

مرکز جرم دستگاهی از ذرات، نقطه ای است که در موقعحرکتکردن گویی تمام جرم دستگاه در آنجا متمرکز شده است و تمام نیروهای خارجی به آن نقطه اثر می کنند. مرکز جرم یک دستگاه شامل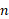 ذره ، نقطه ای است که مختصات آن ازمعادله های زیر به دست می آیند.

(1)

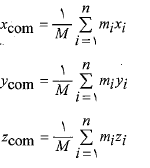
یا

(2)

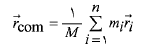
در این معادله ها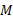 جرم کل دستگاه است.

مسئله نمونه- مرکز جرم سه ذره

سه ذره به جرم های ,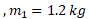 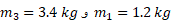 یک مثلث سه ضلع برابر به ضلع 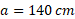تشکیل می دهند. مرکز جرم این دستگاه سه ذره ای در کجا قرار دارد؟

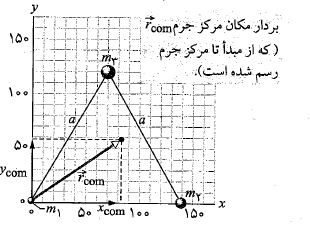
محاسبات: محورهای 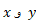 را می توان طوری انتخاب کرد که یکی از ذره ها در مبدا مختصات و محور 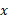در راستای یکی از ضلع های مثلث. در نتیجه مختصات سه ذره مطابق جدول زیر خواهند بود:

جرم کل دستگاه 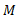برابر با 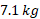است. مختصات مرکز جرم عبارت  اند از

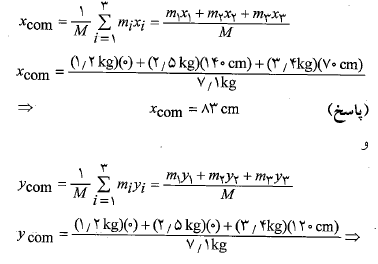
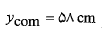
در شکل مرکز جرم با بردار مکان مشخص شده که دارای مولفه های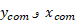 است. اگر سمت گیری دیگری از دستگاه مختصات را انتخاب می کردیم، این مختصه ها تفاوت می گردند، اما محل مرکز جرم نسبت به ذره ها همان می شد.

قانون دوم نیوتون درباره دستگاه ذرات

حرکت مرکز جرم دستگاه ذرات از قانون دوم نیوتون درباره دستگاه ذرات پیروی می کند، که مبتنی بر معادله زیر است

(3)

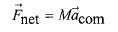
در اینجا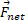 برایند نمام نیروهای خارجی وارد شده به دستگاه، 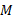جرم کل و شتاب مرکز جرم دستگاه است.

تکانه ی خطی و قانون دوم نیوتون

کمیت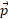 را تکانه خطی تک ذره می نامند و از معادله زیر به دست می آید

(4)

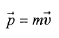
قانون دوم نیوتون را بر حسب تکانه خطی می توان چنین نوشت

(5)

در معادله بالا برای دستگاه ذرات به صورت زیر در می آیند.

(6) و(7)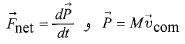

مسئله نمونه- حرکت مرکز جرم سه ذره

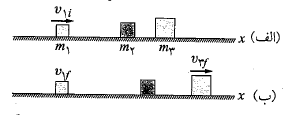
اگر در یک دستگاه همه ذرات با هم حرکت کنند، مرکز جرم هم بی شک با آن ها حرکت می کند. اما اگر ذرات با شتاب های مختلف در جهت های متفاوت حرکت کنند، چه می شود؟ سه ذره در قسمت الف شکل در آغاز به حال سکون قرار دارند. هر کدام از سه ذره از سوی اجسام بیر.ن این دستگاه تحت اثر یک نیروی خارجی قرار م یگیرندجهت نیروها در شکل نشان داده شده و بزرگی آن ها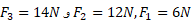 است. مرکز جرم این دستگاه چه شتابی دارد و در چه جهتی حرکت می کند؟

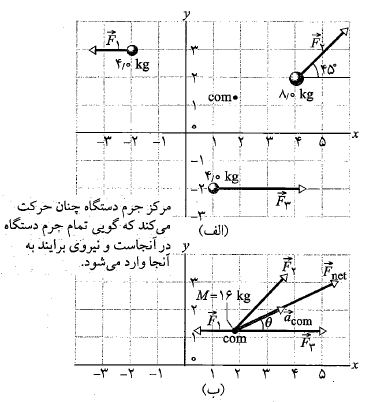
محاسبات: می توانقانون دوم نیوتون را درباره مرکز جرم به کاربرد وچنین نوشت

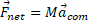
یا

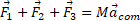
و از آنجا داریم

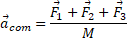
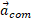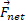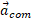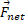معادله های فوق نشان می دهند که شتاب مرکز جرم همسو با نیروی خارجی برایند وارد شده به دستگاه است قسمت ب شکل. چون ذره ها در آغاز ساکن اند مرکز جرم هم باید در حال سکون باشد. همین که مرکز جرم شروع به شتاب گرفتن کرد، حرکتش باید در جهت مشترک و باشد.

برای مولفه های مربوط به محور 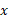 داریم

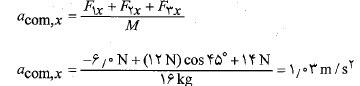
همچنین برای مولفه های مربوط به محور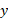 داریم

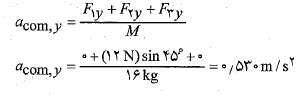
با استفاده کردن از این مولفه ها بزرگی شتاب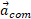 چنین به دست می آید

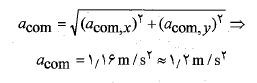
زاویه بردار شتاب ( نسبت به محور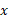 مثبت) برابر است با

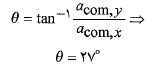
برخورد و ضربه

با استفاده کردن ازقانون دوم نیوتوندر شکل تکانه برای یک جسم ذره مانند درگیر در برخورد، به قضیه ضربه- تکانه خطی منجر می شود:

(8) و (9)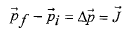

که در آن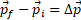 تغییر تکانه خطی جسم و 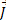ضربه ناشی از نیروی 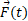است که در حین برخورد از یک جسم به جسم دیگر وارد می شود:

(10)

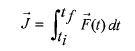
اگر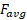 بزرگی متوسط 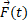در حین برخورد و 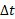مدت زمان برخورد باشد، برای برخورد یک بُعدی داریم

(11)

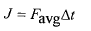
وقتی جریان پایایی از اجسام، هر یک به جرم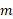 و تندی، با جسم ثابت شده در محلی برخورد می کند، نیروی متوسط وارد شده به جسم ثابت برابر است با

(12)

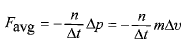
که در آن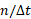 آهنگ برخورد اجسام با جسم ثابت و 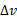تغییر سرعت هر جسم برخورد کننده است. این نیروی متوسط می تواند از معادله زیر هم به دست آید

(13)

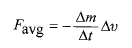
که در آن آهنگ برخورد مقدار جرم با جسم ثابت است. در معادله (12) و (13)، اگر اجسام بر اثر برخورد متوقف شوند، داریم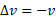 و اگر آن ها بدون تغییر تندی به طور مستقیم به پس سو برگردند، داریم.

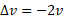مسئله نمونه- ضربه دو بُعدی، برخورد خودرو مسابقه – دیوار

قسمت الف شکل نمای مسیر یک خودرو مسابقه را در هنگام برخورد با دیوار کنار مسیر، با دید از بالا نشان می دهد. درست پیش از برخورد خودرو با تندی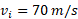 در مسیر خط راستی تحت زاویه 30 درجه نسبت به دیوار حرکت می کند. درست پس از برخورد خودرو با تندی 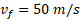در مسیر خط راستی تحت زاویه 10 درجه نسبت به دیوار به حرکت ادامه می دهد. جرم راننده 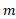برابر با 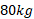است.

الف) در این برخورد ضربه وارد شده به راننده چیست؟

ضربه: بنابراین برابر است با

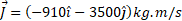
و بزرگی ضربه چنین به دست م یآید

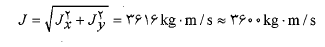
زاویه از رابطه زیر به دست می یابد

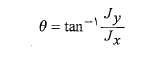
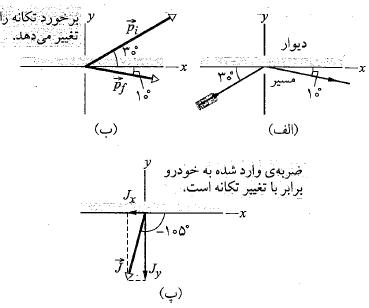
برای مشخص کردن نتیجه درست مولفه های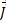 را رسم می کنیم قسمت پ شکل. نتیجه می گیریم مقدار واقعی 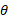برابر است با 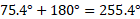، که آن را می توان به صورت زیر نوشت

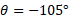
ب) این برخورد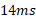 طول می کشد. بزرگی نیروی متوسط وارد شده به راننده در این برخورد چقدر است؟

با توجه به معادله 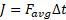 ، بزرگی نیروی متوسط 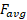از نسبت بزرگی ضربه 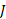، به مدت زمان برخورد 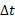به دست می آید.

محاسبات: داریم

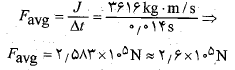
با استفاده کردن از معادله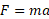 به ازای 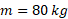می توان نشان داد که بزرگی شتاب متوسط راننده در حین برخورد در حدود 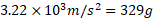است، که شتابی مرگ بار است.

پایستگی تکانه خطی

اگر دستگاهی منزوی باشد، به طوری که هیچ نیروی خارجی برایندی به آن وارد نشود، تکانه خطی دستگاه،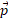، ثابت می ماند:

(14)

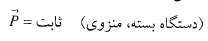
یا

(15)

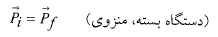
در این معادله شاخص های پایین کمیت 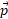 مقادیر آن را در زمان آغازی و زمان بعدی نشان می دهند. معادله های (14) و (15) بیان هایی هم ارز ازقانون پایستگی تکانه خطی هستند.

مسئله نمونه- انفجار یک بُعدی، سرعت نسبی، سفینه فضایی

قسمت الف شکل یک سفینه فضایی با مدول بار آن به جرم کل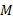 را نشان می دهد، که در فضا در راستای محور 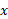حرکت می کند.سرعت آغازی ان ها نسبت به خورشید 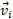 ، دارای بزرگی 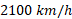است. سفینه با یک انفجار کوچک مدول بار به جرم  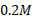را پرتاب می کند قسمت ب شکل.

پس از آن سفینه با تندی ای به اندازه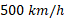 بیشتر از تندی مدول بار در راستای محور 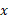حرکت می کند؛ یعنی تندی نسبی 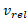، میان سفینه و مدول 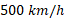است. در این صورت 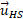سرعت سفینه نسبت به خورشید چقدر است؟

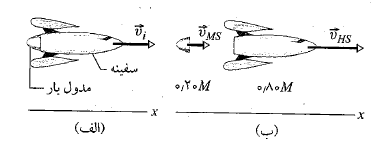
محاسبات: چون حرکت در راستای یک تک محور صورت می گیرد، تکانه ها و سرعت ها را با استفاده کردن از یک علامت برای مشخص کردن جهت می توان بر حسب مولفه های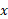 آن ها نوشت. پیش از پرتاب شدن مدول بار داریم

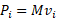
سرعت پرتاب شدن مدول نسبت به خورشید را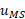 می گیریم. در این صورت تکانه خطی کل دستگاه پس از پرتاب شدن برابر است با

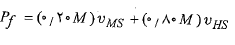
که در آن جمله اول راست معادله، تکانه خطی مدول و جمله دوم تکانه خطی سفینه است.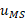 را به صورت زیر می توان به سرعت های معلوم ربط داد 

این رابطه بر حسب نمادهای سرعت ها چنین نوشته می شود

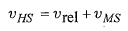
یا

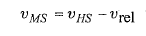
با جانشانی های انجام شده داریم

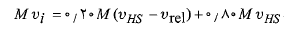
که از آنجا خواهیم داشت

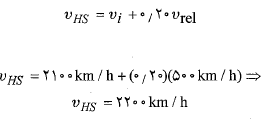
برخورد ناکشسان یک بُعدی

در برخورد ناکشسان میان دو جسمانرژی جنبشی دستگاه دو جسمی پایسته نیست. اگر دستگاه بسته و منزوی باشد، تکانه خطی کل دستگاه باید پایسته باشد. این  مفهوم به صورت برداری زیر نوشته می شود

(16)

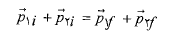
در اینجا شاخص های پایین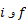 مقادیر پس و پیش از برخورد را نشان می دهند. اگر اجسام در راستای یک محور حرکت کنند، برخورد یک بُعدی است و معادله (16) را بر حسب مولفه های سرعت در راستای آن محور می توان چنین نوشت

(17)

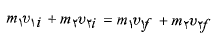
اگر اجسام پس از برخورد به هم بچسبند، برخورد از نوعبرخورد ناکشسان کامل است و اجسام دارای سرعت پایانی یکسان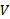 خواهند بود ( چون به هم چسبیده اند).

حرکت مرکز جرم

مرکز جرم یک دستگاه بسته و منزوی شامل دو جسم برخورد کننده، تحت تاثیر برخورد قرار نمی گیرند. یعنی سرعت مرکز جرم 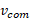 ، بر اثر برخورد تغیر نمی کند.

برخوردهای کشسان یک بُعدی

برخورد کشسان نوع ویژه ای از برخورد است که در آن انرژی جنبشیدستگاه اجسام برخورد کننده پایسته است. اگر دستگاه بسته و منزوی باشد، تکانه خطی آن نیز پایسته است. در برخوردیک بُعدی که در آن جسم2 هدف و جسم 1 یک پرتابه برخورد کننده است، با استفاده کردن از پایستگی انرژی جنبشی و تکانه خطی، سرعت های دو جسم، بی درنگ پس از برخورد چنین به دست می آیند

(18)

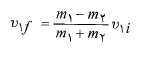
(19)

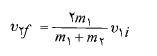
برخوردهای دو بُعدی

اگر دو جسم با هم برخورد کنند وحرکت آن ها در راستای یک محور صورت نگیرد ( برخورد غیر شاخ به شاخ)، برخورد دو بُعدی است. اگر دستگاه دو جسمی بسته و منزوی باشد، قانون پایستگی تکانه برای برخورد صادق است و به صورت زیر بیان می شود.

(20)

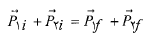
با بیان کردن این قانون برحسب مولفه ها، دو معادله ( برای هریک از دو بُعد یک معادله) به دست می آید، که برخورد را توصیف می کنند. اگر برخورد کشسان ه باشد ( درحالتی خاص) ، پایسته بودن انرژی جنبشی در حین برخورد، معادله سوم زیر را هم بدست می دهد:

(21)

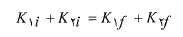
مسئله نمونه- واکنش زنجیری برخوردهای کشسان

در شکل زیر قسمت الف جسم 1 با سرعت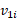 به خط مشترک دو جسم ساکن نزدیک می شود. این جسم با جسم 2 برخورد می کند، که آن هم با جسم 3 به جرم 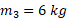 برخورد می کند. پس از برخورد دوم جسم 2 باز هم ساکن م یماند و جسم 3 دارای سرعت 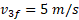می شود مانند شکل قسمت (ب). فرض کنید برخوردها کشسان اند. جرم های اجسام 1و2 چقدر است؟ سرعت پایانی 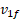جسم 1 چیست؟

محاسبات: اگر از برخورد اول شروع کنیم، عده ی زیادی مجهول داریم که باید به دست آوریم: جرم ها یا سرعت های پایانی اجسام را نمی دانیم. بنابراین از برخورد دوم شروع می کنیم که در آن جسم2 به خاطر برخورد با جسم 3 متوقف می شود. داریم

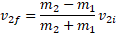
که در آن 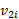 سرعت جسم 2 درست پیش از برخورد و 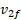سرعت آن پس از برخورد است. با جانشانی 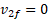( چون جسم 2 متوقف می شود) وسپس 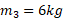داریم

پاسخ:

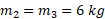
برای برخورد دوم داریم

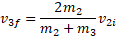
که در آن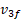 سرعت پایانی جسم 3 است. با جانشانی 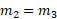و معلوم بودن 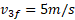داریم

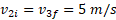
اکنون برخورد اول را در نظر می گیریم اما باید مواظب نمادگذاری مربوط به جسم2 باشیم. سرعت این جسمv2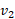، درست پس از برخورد اول برابر با سرعتv2i ( مساوی با5 m/s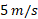) درست پیش از برخورد دوم است. با استفاده کردن از مقدار معلوم  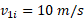داریم

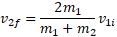
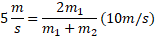
که از آنجا مقدار زیر به دست می آید

پاسخ:

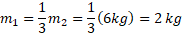
سرانجام برای برخورد اول با این نتیجه و مقدار معلوم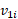 می توان نوشت

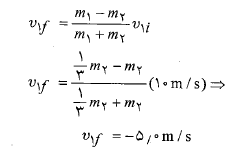
دستگاه های با جرم متغیر

در نبود نیروهای خارجی یک موشک با آهنگ لحظه ای زیر شتاب پیدا می کند

(22)

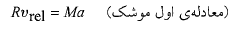
در این معادله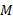 جرم لحظه ای موشک ( از جمله جرم سوخت مصرف نشده)، 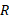آهنگ مصرف سوخت و 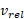تندی خروج گازها نسبت به موشک است. جمله 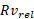را پیش ران موتور موشک می نامند. برای یک موشک با 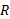و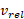 ثابت، که تندی اش از 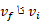و جرمش از 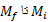تغییر می کند، داریم

(23)

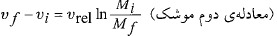
مسئله نمونه- موتور موشک، پیش ران، شتاب

موشکی با جرم آغازی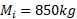 سوخت را با آهنگ 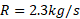مصرف می کند. تندی گازهای خروجی 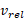نسبت به موتور موشک 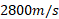است. الف) پیش ران تولید شده توسط موتور موشک چقدر است؟

محاسبه:

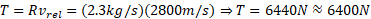
ب) تاب آغازی موشک چقدر است؟

با استفاده کردن از معادله که در آن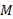 جرم موشک است، می توان پیش ران 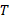را به بزرگی شتاب حاصل 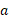، ربط داد. اما وقتی سوخت مصرف می شود، 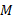کاهش و 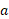افزایش می یابد. چون 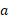شتاب آغازی موشک را می خواهیم، باید از مقدار جرم آغازی 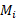استفاده کنیم.

محاسبه:

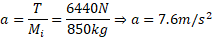
موشک برا یپرتاب شدن از سطح زمین باید شتابی بیش از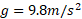 داشته باشد. به عبارت دیگر پیش ران 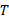باید از نیروی گرانشی آغازی وارد شده به موشک بیشتر باشد، که در اینجا بزرگی آن 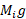برابر است با

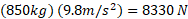
چون شتاب یا پیش ران لازم در اینجا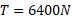 تامین نمی شود، موشک به خودی خود نمی تواند از زمین بلند شود و به موشک توانمند دیگری نیاز است.

برای مطالعه مباحث بیشتر از محصول دوره آموزشی فیزیک عمومی 1 استفاده کنید.