توان

آهنگ زمانی انجام دادن کار بوسیله یک نیرو را توان ناشی از نیرو می نامند. اگر مقدار کار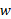  در مدت زمان 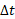 توسط نیرو انجام شود، توان متوسط ناشی از نیرو در این بازه زمانی برابر است با

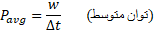
توان لحظه ای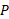 ، آهنگ زمانی لحظه ای انجام دادن کار است که معادله آن چنین است

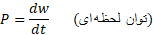
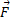مثال خودرو وانت شکل زیر نیروی  را به اتاق یدک وارد می کند و آن را در لحظه معینی با سرعت 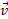 می کشد. توان لحظه ای ناشی از نیروی 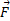 برابر با آهنگ کار انجام شده توسط نیروی 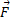 در آن لحظه روی اتاق یدک است و از معادله های

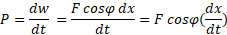
یا

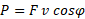
و

به دست می آید. اگر بگوییم که این توان«توان وانت» است، اغلب پذیرفتنی است،اما باید بدانیم که: توان آهنگی است که با آن نیروی وارد شده کار انجام می دهد.

مسئله نمونه – توان، نیرو، سرعت

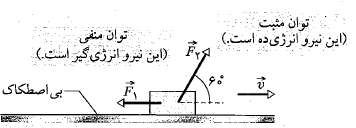
در اینجا کار لحظه ای یعنی آهنگ انجام دادن کار در هر لحظه معین را به جای آهنگ متوسط انجام دادن کار در یک بازه زمانی حساب می کنیم. شکل زیر نیروهای ثابت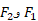  را نشان می دهد، که به جعبه ای در هنگام لغزیدن بر روی یک سطح افقی بی اصطکاک به سمت راست، وارد می شوند. نیروی 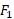 افقی به بزرگی 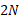 و نیروی 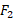 که تحت زاویه 60 درجه نسبت به سطح به بالاسو اثر می کند دارای بزرگی 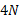 است. تندی جعبه ، در لحظه معینی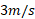 است. توان ناشی از هر نیرو که در آن لحظه به جعبه اثر می کند و هم چنین، توان خالص چقدر است؟ آیا توان خالص در آن لحظه تغییر می کند؟

محاسبه: در مورد نیروی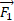  که با بردار سرعت 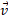 زاویه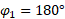  می سازد داریم

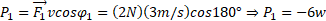
این نتیجه نشان می دهد که نیروی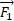  انرژی را با آهنگ 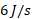 از جعبه می گیرد. برای نیروی 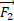 که با بردار سرعت 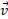 زاویه 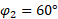  می سازد داریم

این نتیجه مثبت نشان می دهد که نیروی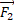  انرژی را با آهنگ 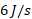 به جعبه می دهد.

توان خالص برابر با مجموع توان های فردی است:

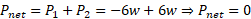
این نتیجه نشان می دهد که آهنگ خالص دادن انرژی به جعبه یا گرفتن انرژی از آن، صفر است. بنابراین انرژی جنبشی جعبه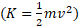  تغییر نمی کند و به همین دلیل تندی جعبه در همان مقدار 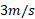 باقی می ماند. چون  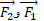  و سرعت 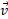 تغییر نمی کنند، با توجه به معادله  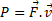  معلوم می شود که 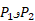 ثابت اند و در نتیجه  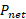 نیز ثابت است.

قضیه کار و انرژی جنبشی

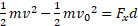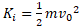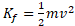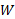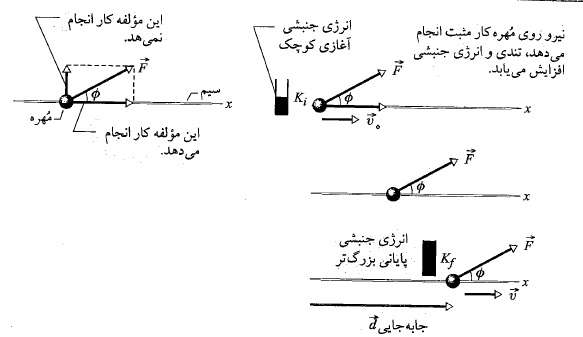
معادله  تغییر انرژی جنبشی مهره ( از مقدار آغازی  تا مقدار پایانی  ) را به  ( مساوی با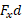 ) ، کار انجام شده روی مهره ربط می دهد.

برای اشیای ذره مانند معادله یاد شده را می توان تعمیم داد. فرض کنید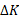  تغییر انرژی جنبشی شیء و 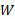 کار انجام شده روی آن باشد. در این صورت می توان نوشت

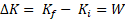
که نشان می دهد:

(کار خالص انجام شده روی ذره)=(تغییر انرژی جنبشی یک ذره)

هم چنین می توان نوشت

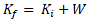
که نشان می دهد:

(کار خالص انجام شده)+(انرژی جنبشی پیش از انجام شدن کار خالص)=(انرژی جنبشی پس از انجام شدن کار خالص)

قضیه کار-انرژی برای کارهای مثبت ومنفی، هر دو، معتبر است. کار خالص انجام شده روی یک ذره، اگر مثبت باشد، انرژی جنبشی ذره به اندازه کار انجام شده افزایش و اگر منفی باد، انرژی جنبشی ذره به اندازه کار انجام شده کاهش می یابد.

به عنوان مثال،اگر انرژی ذره ای در آغاز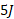  و انتقال خالص انرژی به ذره 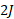 ( کار خالص مثبت)باشد، انرژی جنبشی پایانی ذره 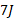 خواهد بود. اما اگر انتقال خالص انرژی از ذره 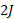 ( کار خالص منفی) باشد، انرژی جنبشی پایانی ذره 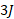 خواهد بود.

مسئله نمونه- کار انجام شده توسط دو نیروی ثابت، جاسوس های صنعتی

در شکل زیر قسمت الف دو مامور مخفی یک گاو صندوق 225 کیلوگرمی را که در آغاز ساکن است، به اندازه جابه جایی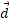   به بزرگی 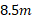 در روی یک سطح افقی به سمت کامیونی می لغزانند. مامور 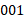 گاو صندوق را با نیروی 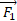 به بزرگی 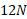 تحت زاویه 30 درجه پایین سوی افقی هل می دهد و مامور 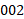 گاوصندوق را با نیروی 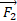 به بزرگی 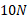 تحت زاویه 40 درجه بالای سوی افقی، می کشد. بزرگی و جهت این نیروها در حین حرکت کردن صندوق تغییر نمی کند و تماس سطح با گاو صندوق بی اصطکاک است.

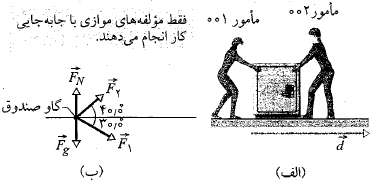
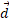الف)کار خالص انجام شده رویگاو صندوق توسط نیروهای  در طی جابه جایی  چیست؟

حل: با استفاده ازمعادله 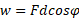  و با توجه به نمودار جسم -آزاد مربوط به گاو صندوق در قسمت (ب) شکل کار انجام شده توسط 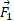 برابر است با

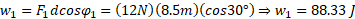
و کار انجام شده توسط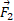  برابر است با

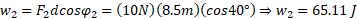
بنابراین کار خالص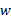  برابر است با

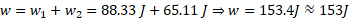
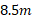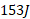پس، دو مامور با جابه جا کردن گاو صندوق به اندازه  انرژی  را به انرژی جنبشی گاو صندوق تبدیل می کنند.

ب) در حین جابه جایی،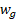  کار انجام شده روی گاو صندوق توسط نیروی گرانشی  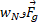، کار انجام شده روی گاو صندوق توسط نیروی عمودی 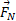 ناشی از سطح چقدر است؟

محاسبات : چون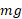  بزرگی نیروی گرانشی است، داریم

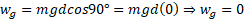
و

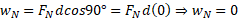
این نتیجه ها را باید از پیش می دانستیم. چون این نیروها بر جابه جایی گاو صندوق عمودند، کاری که روی گاو صندوق انجام می دهند صفر است و با گاو صندوق هیچ گونه انرژی ای مبادله نمی کنند.

پ)گاو صندوق در آغاز ساکن است. تندی آن، در پایان جابه جایی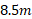  چقدر است؟

چون نیروهای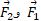  به گاو صندوق انرژی منتقل می کنند و انرژی آن را تغییر می دهند، تندی گاو صندوق تغییر می کند.

حل: با ترکیب کردن معادله های قضیه کار-انرژی جنبشی و تعریف انرژی جنبشی بدست می آید:

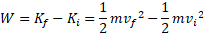
تندی آغازی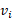  صفر است، و می دانیم که کار انجام شده  است. پس با حل کردن معادله بالا نسبت به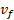  و جانشانی داده های معلوم داریم

مسئله نمونه- کار انجام شده توسط نیروی ثابت به صورت نمادگذاری بردارهای یکه

در یک روز توفانی صندوق محتوای پارچه ای روی کف روغنی و لیز پارکینگی لغزانده می شود و در حالی که صندوق جابه جایی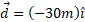  را انجام می دهد باد با نیروی

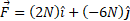
با حرکت صندوق مخالفت می کند. وضعیت حرکت صندوق و محورهای مختصات در شکل نشان داده شده اند.

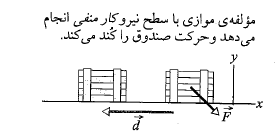
الف) نیروی باد در حین جابه جایی صندوق چه کاری انجام می دهد؟

محاسبات: می توانیم بنویسیم

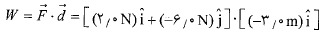
از حاصل ضرب های ممکن بردارهای یکه، فقطk.kوj.j,i.i  ناصفراند. بنابراین داریم

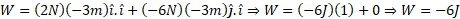
پس نیرو به اندازه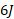  روی صندوق کار منفی انجام می دهد، یعنی 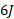 انرژی جنبشی از صندوق گرفته می شود.

ب) اگر انرژی جنبشی صندوق در آغاز جابه جایی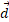  برابر با 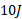 باشد، انرژی جنبشی آن در پایان جابه جایی 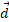 چقدر است؟

محاسبه: با استفاده کردن از قضیه کار-انرژی به صورت معادله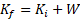  داریم

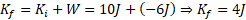
انرژی جنبشی کمتر به این معنی است که تندی صندوق کم شده است.

کار و نیروهای پایستار

کار انجام شده توسط نیروی گرانشی

کار انجام شده روی یک شی توسط نیروی گرانشی وارد شده به شی را بررسی می کنیم. شکل زیر یک گوجه فرنگی به جرم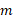  را نشان می دهد که با تندی آغازی 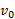 و با انرژی جنبشی آغازی 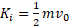 به طور قائم به بالاسو پرتاب شده است.

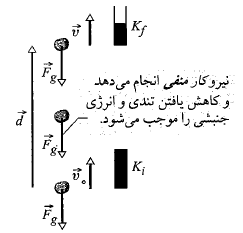
وقتی گوجه فرنگی بالا می رود حرکتش توسط نیروی گرانشی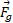  کُند می شود، یعنی بخاطر کاری که  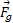 روی گوجه فرنگی انجام می دهد انرژی جنبشی آن کم می شود.  چون گوجه فرنگی به صورت یک ذره در نظر گرفته می شود، برای محاسبه کار انجام شده در طیجابه جایی 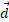 می توان از معادله 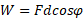 استفاده کرد. به جای بزرگی 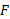، مقدار 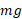 را که بزرگی 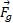 است، قرار می دهیم. در نتیجه، 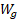 کار انجام شده توسط نیروی گرانشی 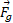 برابر است با

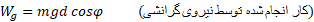
در مورد شیئی که بالا می رود نیروی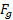  مطابق شکل در جهت مخالف جابه جایی 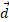 وارد می شود. بنابراین به ازای 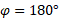 داریم

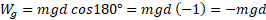
علامت منفی کار نشان می دهد که وقتی شی بالا می رود، نیروی گرانشی وارد شده به آن مقدار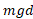  را از انرژی جنبشی شیء می گیرد. این موضوع با کُند شدن حرکت در هنگام بالا رفتن شی سازگار است. شی پس از رسیدن به بیشینه ارتفاع به پایین سقوط می کند و 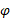 زاویه میان نیروی 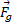 و جابه جایی 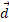 صفر می شود. بنابراین می توان نوشت:

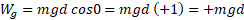
علامت مثبت کار نشان می دهد که نیروی گرانشی در این حالت مقدار انرژی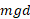  را به انرژی جنبشی شی در حال سقوط می دهد. (البته که تندی شی افزایش می یابد).

مسئله نمونه – کار انجام شده در هنگام بالا کشیدن سورتمه از یک شیب برفی

در این مسئله شی در راستای یک شیب راهه کشیده می شود، اما در آغاز و در پایانحرکت ساکن است، و از این رو انرژی جنبشی اش تغییر نمی کند. قسمت الف شکل زیر این وضعیت را نشان می دهد. طنابی سورتمه 200 کیلوگرمی را از شیب راهه ای با زاویه شیب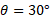  در طی مسافت 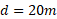 به سمت بالا می کشد. جرم کل سورتمه و محتویات آن 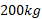 است. شیب برفی چنان لغزنده است که می توان آن را بی اصطکاک در نظر گرفت. چقدر کار توسط هریک از نیروهای وارد شده به سورتمه انجام می شود؟

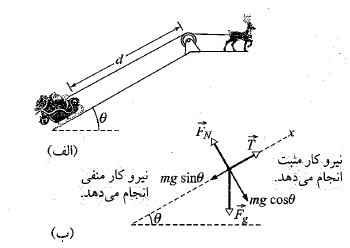
همانند قسمت ب شکل یک نمودار جسم آزاد رسم می کنیم که نیروی گرانشی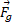 ، نیروی کشش طناب   و نیروی عمودی وارد شده از سوی سطح شیب دار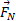  را نشان می دهد.

نیروی عمودی اثری در حرکت سورتمه ندارد و کار آن صفر است. به طور صوری تر با استفاده کردن از معادله

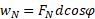 می توان نوشت:  

پاسخ:

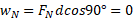
می دانیم که مولفه نیروی گرانشی در راستای سطح شیب دار دارای بزرگی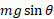  و به پایین سوی سطح است. بنابراین، بزرگی این مولفه برابر است با

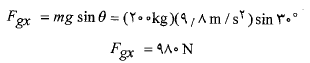
زاویه میان جابه جایی و این مولفه نیرو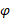  برابر با 180 درجه است. بنابراین با استفاده کردن از معادله 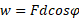 می توان نوشت:

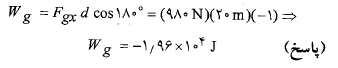
علامت منفی نشان می دهد که نیروی گرانشی انرژی را از سورتمه می گیرد.

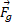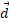روش هم ارز، روش دیگری است برای به دست آوردن این نتیجه کاربرد نیروی گرانشی کامل  و  برابر با 120 درجه است ( زاویه شیب 30 درجه را با زاویه 90 درجه جمع کنید). در نتیجه با استفاده کردن از معادله فوق داریم

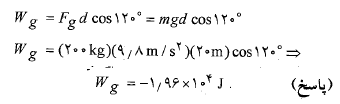
برای محاسبه نیروی کشش طناب دو روش وجود دارد. استفاده کردن از قضیه کار-انرژی جنبشی معادله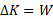  است، که در آن ، کار خالص انجام شده توسط نیروها برابر با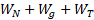  است و تغییر انرژی جنبشی 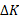 صفر است (زیرا انرژی های آغازی و پایانی با هم برابر یعنی صفر هستند). بنابراین با استفاده کردن از معادله 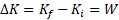 داریم

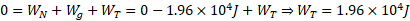
به جای انجام دادن این کار می توان قانون دو نیوتن درباره حرکت در راستای محور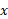  را به کار برد و بزرگی نیروی کشش طناب 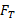 را پیدا کرد. با فرض صفر بودن شتاب در راستای شیب ( به جز در لحظه های کوتاه آغاز کردن و توقف) می توان نوشت:

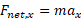
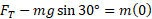
در نتیجه بزرگی نیروی مورد نظر برابر است با

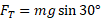
چون این نیرو و جابه جایی هر دو به سوی بالای شیب هستند، زاویه میان این دو بردار صفر است. بنابراین اکنون برای پیدا کردن کار انجام شده توسط نیروی کشش طناب می توان معادله زیر را به کار برد:

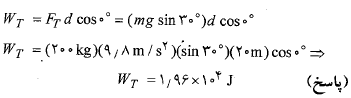
کار انجام شده توسط نیروی فنر

نیروی ناشی از فنر برابر است با

که در آن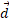  جابه جایی سرآزاد فنر نسبت به حالت آرامش فنر ( حالت بدون تراکم و بدون کشیدگی) و 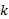 ثابت فنر( معیاری برای سفتی فنر) است. اگر محور 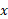 در راستای فنر و مبدا مختصات در مکان سرآزاد و فنر در حالت آرامش باشد می توان نوشت

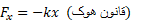
بنابراین نیروی فنر یک نیروی متغیر است: این نیرو با جابه جایی سر آزاد فنر تغییر می کند. اگر شیئی به سرآزاد فنر وصل شود، در هنگام حرکت کردن شیء از مکان آغازی 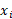  تا مکان پایانی 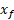 کار انجام شده توسط نیروی فنر روی شیء 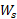 برابر است با

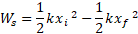
به ازای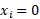  و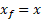  ، معادله بالا به صورت زیر در می آید

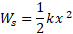
مسئله نمونه – کار انجام شده توسط فنر برای تغییر دادن انرژی جنبشی

وقتی فنری روی یک شیء کار انجام می دهد، به سادگی نمی توان کار را با ضرب کردن نیروی فنر در جابه جایی شیء به دست آورد. دلیل آن این است که برای نیرو یک مقدار ثابت وجود ندارد و نیرو تغییر می کند. اما جابه جایی را می توان به عده ای بی نهایت بخش کوچک تقسیم کرد و از این رو نیرو در هر بخش به تقریب ثابت است. عمل انتگرال گیری کارهای انجام شده مربوط به بخش ها را با هم جمع می کند. در اینجا از نتیجه سادهانتگرال گیری استفاده می کنیم.

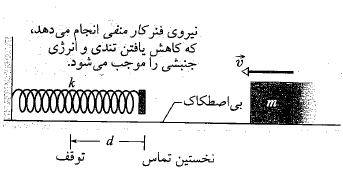
در شکل زیر یک قوطی محتوی زیره سبز به جرم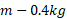  با تندی 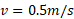 بر روی سطح یک پیشخوان بی اصطکاک می لغزد. این قوطی به فنری با ثابت فنر 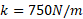 می رسد و آن را متراکم می کند. وقتی قوطی به طور لحظه ای توسط فنر متوقف می شود، اندازه متراکم شدن فنر 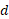 چقدر است؟

حل: رابطه قضیه کار- انرژی مربوط به قوطی چنین نوشته می شود

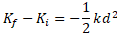
اگر جانشانی را با توجه به اینکه مقدار آغازی انرژی جنبشی قوطی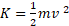  و مقدار آن در هنگام توقف لحظه ای قوطی صفر انجام دهیم، خواهیم داشت:

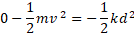
پس از ساده کردن رابطه جانشانی داده ها و حل کردن معادله حاصل نسبت به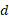  داریم

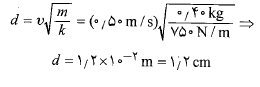
برای مطالعه مباحث پیشرفته از محصول از محصولدوره آموزش فیزیک عمومی 1 استفاده کنید.