گرانش

قانون گرانش

هر ذره در عالم ذره دیگری را با یک نیروی گرانشی جذب می کند که بزرگی اش از معادله زیربه دست می آید

(1-1)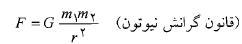

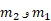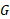که در آن  جرم های ذرات هستند.  فاصله میان ذرات و  ( مساوی با  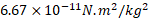) ثابت گرانش است.

رفتار گرانشی پوسته های کروی یکنواخت

نیروی گرانشی میان اجسام گسترده را به طور کلی باید از جمع کردن ( انتگرال گیری) نیروهای فردی وارد شده به ذرات فردی درون اجسام به دست آورد. اما اگر جسم به صورت پوسته کروی یکنواخت یا کره توپر متقارن باشد نیروی گرانشی خالص وارد شده به یک شی بیرونی از سوی آن می تواند به گونه ای که همه جرم پوسته یا جسم در مرکزش قرار داشته باشد محاسبه شود.

اصل بر هم نهی

نیروهای گرانشی از اصل بر هم نهی پیروی می کنند؛ یعنی هرگاه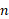  ذره بر هم کنش داشته باشند نیروی خالص 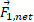 وارد شده به ذره 1 برابر با نجموع نیروهای وارد شده به آن از سوی ذرات فردی دیگر است:

(1-2)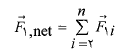

در اینجا مجموع برابر است با جمع برداری نیروهای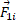  که به ذره 1 از سوی ذره های 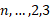 وارد می شوند. نیروی گرانشی 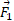  وارد شده به ذره از سوی یک جسم گسترده با تقسیم کردن جسم به اجزاء دیفرانسیلی به جرم 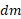، که هر کدام نیروی دیفرانسیلی 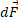 را به ذره وارد می کنند و سپس انتگرال گیری برای تعیین مجموع این نیروها به دست می آید:

(1-3)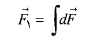

مسئله نمونه- نیروی گرانشی براینددو بُعدی سه ذره

شکل زیر قسمت الف، آرایشی از سه ذره را نشان می دهد که در آن جرم ذره1 برابر با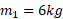 ، جرم ذره های 2و 3 برابر با 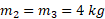 و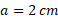  است. نیروی گرانشی 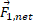 که به ذره1 از سوی ذره های دیگر وارد می شود چیست؟

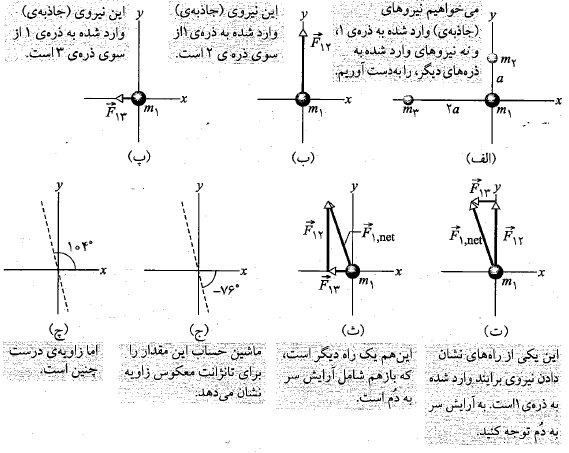
محاسبات: با توجه به معادله(1-1) بزرگی نیروی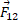  که به ذره 1 از سوی ذره2 وارد می شود برابر است با

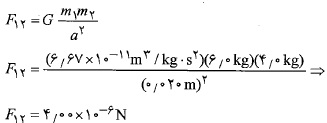
به همین ترتیب بزرگی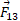  که به ذره 1 از سوی ذره 3 وارد می شود برابر است به

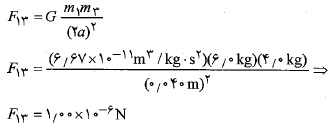
نیروی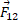  در جهت مثبت محور 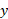 مطابق قسمت ب شکل قرار دارد و فقط دارای مولفه 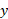 نیرو، یعنی 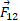 است. به همین ترتیب نیروی 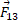 در جهت منفی محور  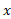قرار دارد و فقط دارای مولفه 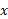 نیرو یعنی 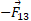  مطابق قسمت پ شکل است. ( به این نکته مهم توجه کنید که : ما در نمودارهای نیرو دُم بردار نیرو را روی ذره ای رسم می کنیم که به آن نیرو وارد می شود. اگر نیروها را به گونه ای دیگر رسم کنیم مرتکب خطا خواهیم شد).

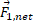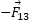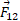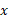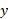برای تعیین نیروی برایند  وارد شده به ذره 1 باید دو نیرو را به صورت برداری با هم جمع کنیم مطابق قسمت ت و ث شکل. ما این کار را با یک ماشین حساب ویژه محاسبات برداری هم می توانیم انجام دهیم. اما در اینجا  و  خود مولفه هایx  وy  نیروی 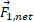  هستند. بنابراین با استفاده از معادله (2-1) ابتدا بزرگی و سپس جهت  را معین م یکنیم. بزرگی این نیرو برابر است با

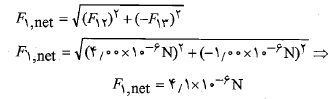
زاویه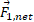  نسبت به محور  مثبت چنین بدست می آید

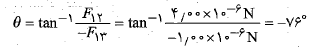
آیا پاسخ به دست آمده منطقی است همانند قسمت ج شکل؟خیر، چون راستای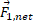  باید در بین راستاهای 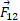 و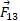  واقع شود. صفحه ماشین حساب تنها یکی از دو پاسخ ممکن تابع 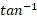 را نمایش می دهد. با افزودن 180 درجه به پاسخ به دست آمده پاسخ دیگری نیز پیدا می شود که برابر است با

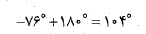
که زاویه ای منطقی برای جهت نیروی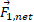  است همانند قسمت چ شکل مسئله.

شتاب گرانشی

شتاب گرانشی 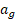  یک ذره ( به جرم 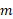 ) فقط از نیروی گرانشی وارد شده به ذره ناشی می شود. اگر ذره در فاصله  از مرکز یک جسم کروی یکنواخت به جرم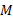  قرار داشته باشد، 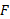 بزرگی نیروی گرانشی وارد شده به ذره از معادله (1-1) به دست می آید. بنابراین با استفاده کردن از قانون دوم نیوتون داریم

(1-4)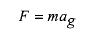

که در آن

(1-5)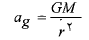

شتاب سقوط آزاد و وزن

چون جرم زمین به طور یکنواخت توزیع نشده است، چون زمین شکل کروی کامل ندارد و چون زمین می چرخد، شتاب واقعی سقوط آزاد یک ذره در نزدیکی زمین 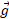 ، با شتاب گرانشی  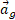  اندکی تفاوت دارد و وزن ذره ( مساوی با 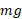 ) با بزرگی نیروی گرانشی وارد شده به آن متفاوت است.

گرانش در درون پوسته کروی

پوسته کروی یکنواخت ماده هیچ نیروی گرانشی برایندی به ذره واقع در درون خود وارد نمی کند. یعنی اگر ذره ای درون یک کره توپر یکنواخت در فاصله  از مرکز کره قرار گیرد، نیروی گرانشی وارد شده به ذره فقط ناشی از جرم درون کره ای به شعاع  ( کره درونی) است. بزرگی این نیرو از معادله زیر به دست می آید

(1-6)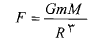

که در آن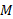  جرم کره و 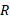 شعاع کره است.

مسئله نمونه- اختلاف شتاب گرانشی میان سر و پا

الف) فضانوردی با قد 1.70 متر در یک شاتل فضایی که در مداری به فاصله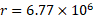  متر از مرکز زمین به دور زمین می گردد بطور «راست قد» قرار دارد. اختلاف شتاب گرانشی میان کف پا و محل سر فضانورد چیست؟

محاسبات: با دیفرانسیل گرفتن از معادله(5-1) داریم

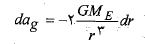
که در آن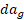  تغییر دیفرانسیل شتاب گرانشی ناشی از تغییر دیفرانسیلی   یعنی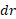  است. در مورد فضا نورد داریم  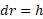  و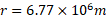 . با جانشانی داده ها در معادله بالا خواهیم داشت

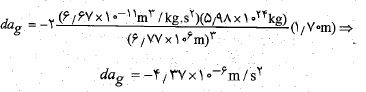
در اینجا مقدار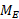  از پیوست پ کتاب فیزیک هالیدی گرفته شده است. این نتیجه نشان می دهد که شتاب گرانشی ( به سوی زمین) در محل پای فضانورد اندکی از شتاب گرانشی ( به سوی زمین) در محل سر او بزرگ تر است. این اختلاف شتاب ( که اغلب اثر کشندی نامیده می شود) تمایل دارد که قد فضا نورد را بکشد، اما اختلاف چنان ناچیز است که او هرگز متوجه این موضوع نمی شود و خیلی کمتر از آن است که درد ایجاد کند.

ب)اکنون اگر فضانورد همین حالت « راست قد» را در گردش بر روی مداری به شعاع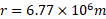  به دور سیاه چاله ای به جرم 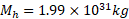 ( که 10 برابر جرم خورشید است) داشته باشد اختلاف شتاب گرانشی میان محل پا و محل سر او چیست؟ سیاه چاله یک سطح ریاضیاتی ( افق رویداد ) به شعاع 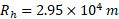 دارد. هیچ چیز حتی نور هم نمی تواند از این سطح یا از جایی واقع در درون آن فرار کند. توجه کنید که فضانورد کاملا در بیرون از سطح ( در فاصله  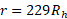 ) قرار دارد.

محاسبات: باز هم باید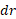 ، تغییر دیفرانسیلی  میان سر فضانورد را به کار برد و از معادله فوق استفاده کرد. اما در اینجا به جای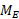  باید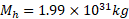  را قرار داد. در نتیجه داریم

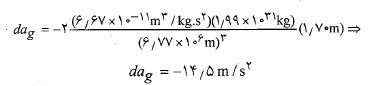
این نتیجه نشان می دهد که شتاب گرانشی ( به سوی سیاهچاله) در محل پای فضانورد نسبت به محل سر او خیلی زیادتر است. نتیجه های حاصل از کشیده شدن بدن تحمل پذیر اما دردآور است. هرگاه فضانورد به سیاهچاله نزدیک تر شود تمایل به کشیده شدن بدن به شدت افزایش خواهد یافت.

انرژی پتانسیل گرانشی

انرژی پتانسیل گرانشیU(r)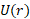  یک دستگاه شامل دو ذره به جرم های  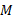 و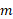  که در فاصله  از هم قرار دارند برابر است با کار انجام شده با علامت منفی توسط نیروی گرانشی وارد شده از سوی یک ذره به ذره دیگر وقتی که فاصله میان دو ذره از بی نهایت ( فاصله خیلی زیاد) تا  تغییر کند. این  انرژی برابر است با

(1-7)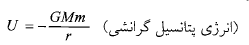

انرژی پتانسیل یک دستگاه

هر دستگاهی شامل بیش از دو ذره باشد انرژی پتانسیل گرانشی کل آن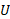  برابر است با مجموعانرژی های پتانسیل مربوط به همه زوج های ذرات. به عنوان مثال برای سه ذره به جرم های 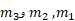 داریم

(1-8)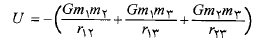

تندی فرار

یک شیء هنگامی می تواند از تاثیر نیروی جاذبه یک جسم نجومی به جرم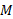  و شعاع 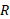 فرار کند ( به فاصله بی نهایت برسد) که تندی آن در نزدیکی سطح جسم دست کم برابر با تندی فرار باشد. این تندی از معادله زیر بدس ت می آید

(1-9)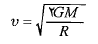

مسئله نمونه- انرژی مکانیکی سیارک در حال سقوط از فضا

سیارکی در حال حرکت کردن یک راست به سوی زمین دارای تندی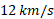  نسبت به زمین است. در این هنگام فاصله سیارک از مرکز زمین 10 برابر شعاع زمین است. با چشم پوشی از اثرهای جو زمین روی سیارک ، تندی سیارک 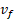، را در موقع رسیدن به سطح زمین پیدا کنید.

محاسبات: فرض کنید جرم سیارک را با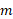  و جرم زمین را با 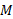 ( مساوی با 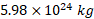( نمایش دهیم. سیارک در آغاز در  فاصله 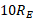 و در پایان در فاصله 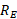 است، که 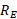 (مساوی با 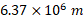) شعاع زمین است. با جانشانی 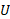 از معادله (7-1) و 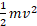  به جای 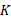 می توان چنین نوشت

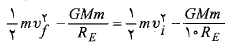
پس از ساده کردن معادله  و جانشانی داده ها داریم

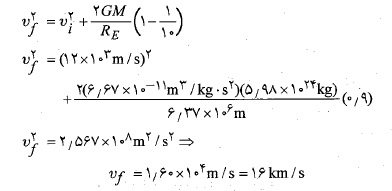
با این تندی سیارک نباید چنان بزرگ باشد که در هنگام برخورد به زمین آسیب قابل ملاحظه ای وارد کند. اگر سیارک فقط 5 متر پهنا داشته باشد، در برخورد با زمین می تواند انرژی ای در حدود انرژی انفجار بمب هسته ای هیروشیما آزاد کند.

قانون های کپلر

حرکتماهواره های طبیعی و مصنوعی از این قانون ها پیروی می کند.

1.قانون مدارها: همه سیاره ها در روی مدارهایی بیضی شکلحرکتمی کنند که خورشید در یکی از کانون های بیضی قرار دارد.

2.قانون مساحت ها: خط وصل کننده هر سیاره به خورشید در زمان های مساوی مساحت های مساوی را جارو می کند ( این گزاره باقانون پایستگی تکانه زاویه ای هم ارز است).

3.قانون دوره های متناوب: مجذور دوره تناوب گردش هر سیاره به دور خورشید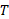 ، با مکعب نیم قطر بزرگ مدار سیاره 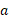، متناسب است. در مورد مدارهای دایره ای به شعاع  می توان نوشت:

(1-10)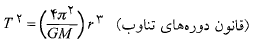

که در آن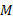  جرم جسم جذب کننده، یعنی خورشید، در حالت مربوط به دستگاه منظومه شمسی است. در مورد مدارهای سیاره ای، نیم قطر بزرگ 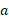 به جای  ، شعاع مدار دایره ای قرار داده می شود.

مسئله نمونه- قانون دوره های تناوب کپلر، دنباله دار هالی

دنباله دار هالی که با دوره دوره تناوب 76 سال به دور خورشید می گردد، در سال 1986/1365 به نزدیک ترین فاصله از خورشید یعنی به فاصله حضیض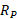  برابر با  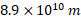 رسیده است.

الف)دورترین فاصله این دنباله دار از خورشید یعنی فاصله اوج آن 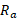   چقدر است؟

محاسبات: با انجام دادن این جانشانی و سپس حل کردن معادله حاصل نسبت به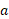  داریم

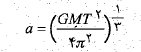
اگر جرم خورشید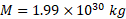  و دوره تناوب دنباله دار 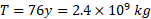 را در معادله بالا جانشانی کنیم، نتیجه می گیریم که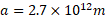. اکنون می توان نوشت

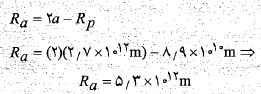
ب) خروج از مرکز مدار دنباله دار هالی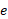  چقدر است؟

محاسبات: داریم

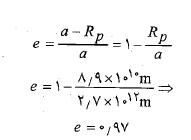
مدار این دنباله دار با خروج از مرکز نزدیک به واحد یک بیضی باریک و کشیده است.

انرژی در حرکت سیاره ای

هر گاه سیاره یا ماهواره ای به جرم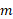  بر روی مداری دایره ای به شعاع  حرکت کند، انرژی پتانسیل آن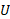 ، وانرژی جنبشی آن 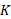 از معادله های زیر به دست می آیند

(1-11 و 1-12)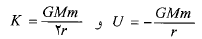

در این صورت انرژی مکانیکی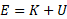   برابر است با

(1-13)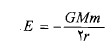

این انرژی برای مدار بیضی شکل با نیم قطر بزرگ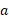  برابر است با

(1-14)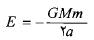

مسئله نمونه- انرژی مکانیکی یک توپ بولینگ در حال دوران

فضانوردی به قصد شوخی یک توپ بولینگ به جرم 7.20 کیلوگرم را در ارتفاع 350 کیلومتر به درون یک مدار دایره ای دور زمین رها می کند.

الف) انرژی مکانیکی توپ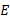 ، درحرکت روی مدار خود چقدر است؟

اگر ابتدا شعاع مداری  را پید کنیم ( که با ارتفاع داده شده برابر نیست) می توانیم انرژی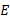  را با استفاده کردن از انرژی مداری داده شده با معادله (13-1) به دست آوریم.

محاسبات: شعاع مدار برابر است با

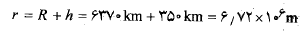
در اینجاR  شعاع زمین است. پس با استفاده کردن از معادله (13-1) وبه ازای جرم زمین برابرباM=5.98×1024 kg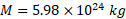  ، انرژی مکانیکی برابر است با

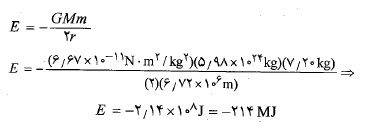
ب) انرژی مکانیکی توپ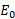  در سکوی پرتاب دماغه کانا ورال چقدر است ( پیش از آن فانورد و فضاپیما پرتاب شده اند)؟ از محل سکو تا روی مدار گردش توپ تغییر انرژی مکانیکی توپ∆E 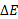 چقدر است؟

در سکوی پرتاپ توپ در مدار گردش قرار ندارد و در نتیجه از معادله (13-1) استفاده نمی شود. در عوض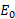  را می توان از معادله 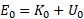 به دست آورد. 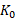 انرژی جنبشی توپ و 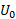 انرژی پتانسیل گرانشی دستگاه توپ-زمین است.

محاسبات: برای تعیین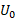  با استفاده از معادله (11-1) می توان نوشت

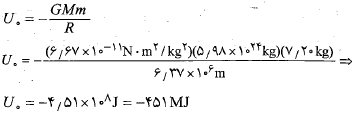
انرژی جنبشی توپ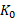  از حرکتکردن توپ با چرخش زمین ناشی می شود. می توان نشان داد که این انرژی کمتر از 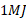 است که نسبت به 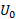 در خور چشم پوشی است. بنابراین انرژی مکانیکی توپ در روی سکوی پرتاب برابر است با

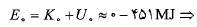
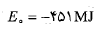
افزایش یافتن انرژی مکانیکی توپ از محل سکوی پرتاب تا مدار برابر است با

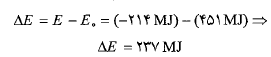
این مقدار انرژی را می توان با صرف کردن چند دلار از شرکت های خدمات عمومی خریداری کرد.واضح است که هزینه بالای قرار دادن اشیاء در مدار گردش به دور زمین مربوط به انرژی مکانیکی مورد نیاز آن ها نیست.

دیدگاه اینشتین درباره گرانش

انیشتین دریافت که گرانش وشتاب هم ارزند. این مفهوم که اصل هم ارزی نامیده می شود، اینشتین را به نظریه ای از گرانش ( نظریه نسبیت عام) رهنمون ساخت که بنا به آن اثرهای گرانشی بر حسب خمیدگی فضا بیان می شوند.

 برای مطالعه مباحث پیشرفته از محصول  دوره آموزشی فیزیک عمومی1 از سایت لینوم استفاده کنید.