فصل دوم: سیستم‌های نیرو

 در آموزش قبلی استاتیک در موردمفاهیم اولیه استاتیک صحبت کردیم. در این آموزشلینومبه بررسیسیستم‌های نیرو می‌پردازیم

انواع نیروها: نیروها را می‌توان به دو شکل زیر طبقه بندی کرد.

1- نیروهای تماسی: در اثر تماس فیزیکی مستقیم ایجاد می‌شوند.

2- نیروهای حجمی: در اثر قرار گرفتن جسم در یک میدان گرانشی، مغناطیسی یا الکتریکی ایجاد می‌شوند.

 

1- بارهای گسترده: در یک طول، سطح یا حجم به جسم وارد می‌شوند.

2- بارهای نقطه ای: اگر ابعاد سطحی که بار به آن وارد می‌شود در مقایسه با سایر ابعاد قابل صرف نظر باشد، آن را به صورتبار نقطه ای درنظر می‌گیریم.

 

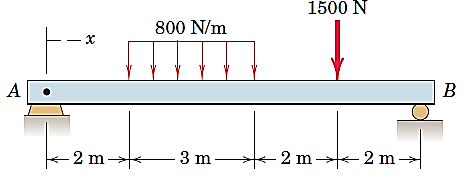
به طور مثال در شکل1 نیروی800 N/m به صورت گسترده در یک طول 3 متری و بار1500 Nبه صورت نقطه به تیر وارد شده است. در فصل 5 بابارهای گسترده به طور کامل آشنا خواهیم شد.

 

شکل 1- نمایش بار نقطه ای و بار گسترده بر تیر

از آنجایی که در درساستاتیک با کمیت‌های برداری مانند نیرو کار می‌کنیم، باید به قوانین حاکم بر این کمیت‌ها تسلط کافی داشته باشیم.

 

بردارها در صفحه

برایند بردارها:برای بدست آوردن برایند دو بردار به روش ترسیمی، از دو روش متوازی الاضلاع و مثلث استفاده می‌کنیم (شکل2). در روش متوازی الاضلاع ابتدا از یک نقطه، هم‌سنگ بردار اول را رسم کرده و از ابتدای آن، هم‌سنگ بردار دوم را رسم می‌کنیم. برای پیدا کردن شکل متوازی الاضلاع، از انتهای بردار اول خطی به موازات بردار دوم رسم می‌کنیم. از انتهای بردار دوم هم خطی به موازات بردار اول می‌کشیم و بدین ترتیب متوازی الاضلاع بدست می‌آید. قطر این متوازی الاضلاع، برایند دو بردار است (شکل2-b).

در روش مثلث، هم‌سنگ بردار اول را از نقطه ای کشیده و از انتهای آن، هم‌سنگ بردار دوم را رسم می‌کنیم. ابتدار بردار اول را به انتهای بردار دوم وصل می‌کنیم و بردار حاصل، همان برایند دو بردار است(شکل2-c). پررنگ بودنV ها در شکل بیانگر این است که اینکمیت‌ها برداری هستند.

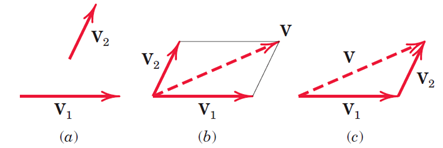
شکل 2-(a) نمایش دو بردار.(b) برایند بردارها به روش متوازی الاضلاع.(c) برایند بردارها به روش مثلث

V= V₁+ V₂برایند بردارهاست.

 

پیدا کردن تفاضل دو بردارV₁وV₂ ،یعنیV₂-V_1،کافیست بردارV₂-را رسم کرده و برایند این بردار وV₁را به کمک یکی از روش‌های ذکر شده بدست آورد.

برای پیدا کردن بردار برایند بیش از دو بردار، هم‌سنگ بردارها را به دنبال هم رسم می‌کنیم (مشابه روش مثلثی).

برداری که ابتدای بردار اول را به انتهای بردار آخر وصل می‌کند، برایند بردارهاست (شکل 3).

 

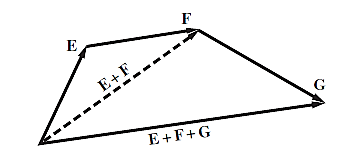
شکل3- نمایش رسم  برایند سه بردار

 

تفاضل بردارها:برای پیدا کردن حاصل تفاضلV₁-V₂ کافیست بردار-V₂ را رسم کرده و سپس به دو روش ذکر شده در پیدا کردن برایند دو بردار، برایند-V₂ وV₁را پیدا کنیم (شکل 4).

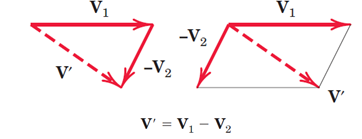
شکل 4- (a)نمایش دو بردار .(b)تفاضل بردارها به روش متوازی الاضلاع. (c) تفاضل بردارها به روش مثلث

 

 

تجزیه بردار ها به مولفه‌های متعامد و غیر متعامد

در قسمت قبل مشاهده شد که می‌توان مجموع دو بردار را بهروش متوازی الاضلاع یا مثلث پیدا کرد. حال در صورتی که دو امتداد متعامد در صفحه و برداری مانندF داشته باشیم، می‌توان آن را مطابق شکل‌5 بر دو امتداد  تجزیه کرد.

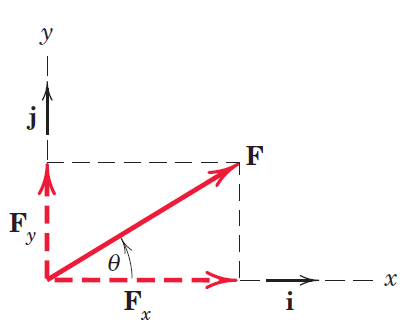
شکل3- تجزیه بردارF به دو بردار متعامدF_{x و}F_y

 

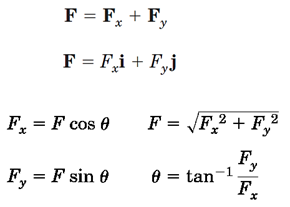
در شکل 6 تجزیه بردارV را بر دو امتداد غیر متعامد 1 و 2 می‌‌بینیم.

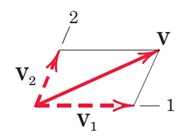
شکل 4- تجزیه بردارV به دو بردار غیر متعامدV₁ وV₂

 

درتجزیه بردار به مولفه‌های غیر متعامد، استفاده از قانون سینوس‌ها و کوسینوس‌ها بسیار کارامد است (شکل7).

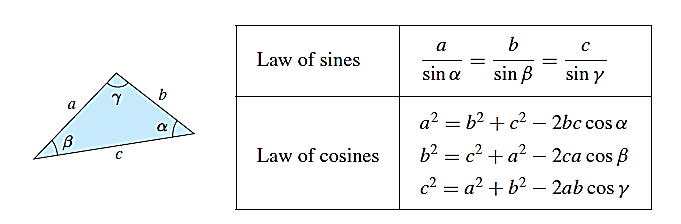
 شکل 5- قانون سینوس‌ها و کوسینوس‌ها در مثلث 

بردارها در فضا

بردارv شکل 8 را در نظر بگیرید.

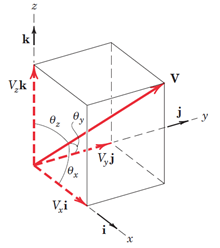
 شکل 6- نمایش بردار در فضا 

 این بردار در هر سه راستایx،y وz مولفه دارد که آنها را باV_xوV_y وV_zنشان می‌دهیم و داریم:

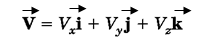
می‌توان نوشت:

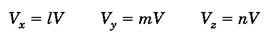
منظور ازl،n وm، کوسینوس‌های هادی (کوسینوس بردارvبا هر یک از سه محورx،y وz) است.

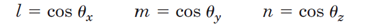
لازم به ذکر است که مجموع مربعات کوسینوس‌های هادی برابر یک است.

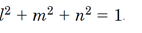
مربع اندازه بردارVبرابر مجموع مربعات اندازه مولفه‌های آن در سه راستاست:

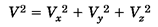
برای حل مسائل سه بعدی معمولا نیاز است که نیرو به صورتبرداری نوشته شود. برای این کار غالبا از دو روش زیر استفاده می‌شود.

1-در صورتی که مختصات دو نقطه از خط اثر نیرویF مشخص باشد، می‌توان بردار یکه راستای نیرو را پیدا و در اندازه نیرو ضرب کرد تا بردار نیرو بدست آید (شکل9).

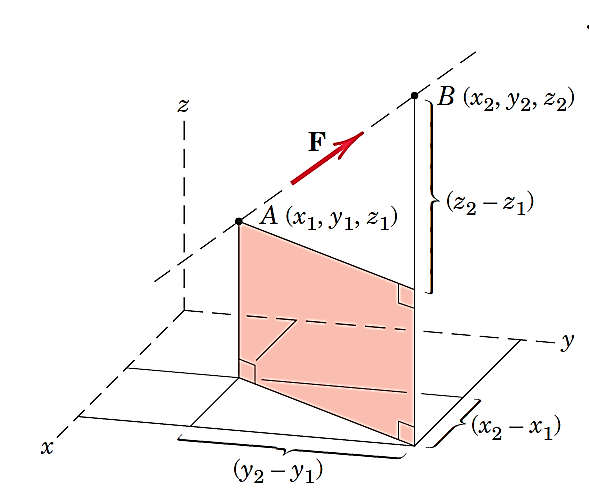
شکل 7- استفاده از مختصات نقاطA وB برای پیدا کردن بردار یکه راستایAB

 

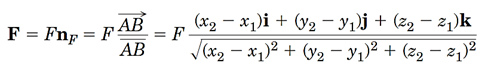
-در روش دوم، دو زاویه ای که جهت خط اثر نیرو را معلوم می‌کنند داریم (شکل 10).

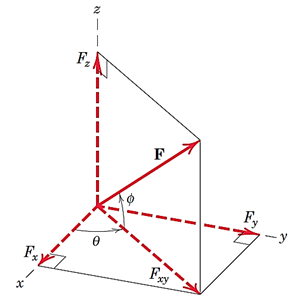
 شکل 8- نوشتن بردار نیرو با داشتن دو زاویه که جهت خط اثر آن را معلوم می‌کنند 

در اینصورت با توجه به شکل داریم:

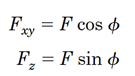
برای تجزیه نیرویFدر صفحهx-y و پیدا کردن مولفه‌هایx وy نیرو می‌توان نوشت:

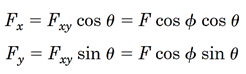
مفهوم گشتاور

وقتی به جسمی نیرو وارد می‌شود، جسم در راستای وارد شدن نیرو تمایل به حرکت پیدا می‌کند. این یکی از اثرات نیرو بر جسم است. اثر دیگر نیرو بر جسم، ایجاد تمایل به دوران جسم حول یک محور است. این محور هر محور غیر موازی و غیر متقاطع با راستای خط اثر نیرو می‌تواند باشد. این تمایل به دوران راگشتاور نیرو یا ممان می‌گویند.

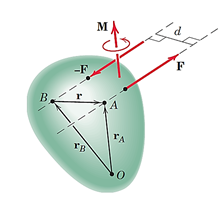
گشتاور نیرو حول یک نقطه

با توجه به شکل 11، بردار گشتاور نیرویF حول نقطهA و یا محورO-Oکه عمود بر صفحه از نقطهA می‌گذرد برابر است با حاصلضرب خارجی بردارr در بردارF. در این رابطه، بردارr بردار موقعیتی است که از نقطهA تا هر نقطه از خط اثر نیرویF رسم می‌شود.

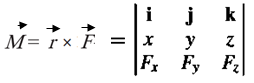
اندازه این عبارت برابر است با

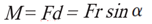
که در آنF، اندازه بردارF وd،بازوی گشتاور، برابرrsinα  است.α زاویه بین بردارr و نیرویF است.

شکل 9- نمایش گشتاور نیرویF حول نقطهA

 

برای تعیین جهت گشتاور، ازقانون دست راست استفاده می‌شود. بدین صورت کهاگر انگشتان دست راست را در جهت بردارrبگیریم و سپس در جهت نیرویF انگشتان را بچرخانیم، انگشت شست جهت بردار گشتاور را نشان خواهد داد. به طور قراردادی، جهت پادساعتگرد (برون سو) گشتاور، مثبت و جهت ساعتگرد (درونسو) منفی در نظر گرفته می‌شود. این قرارداد را می‌توان برعکس درنظر گرفت اما باید توجه داشت که اولا در حل سوال، قراردادی که حل بر مبنای آن انجام شده باید ذکر شود و دوما تا انتهای حل سوال، قرارداد به همان صورت فرض شده حفظ شود.

انتخاب بین روش برداری محاسبه گشتاور و یاروش اسکالر، بستگی به صورت سوال و هندسه آن دارد. معمولا در سوالات سه بعدی، نوشتن بردارهایr وF و استفاده از روش برداری، حل سوال را راحت‌تر می‌کند.

گشتاور نیرو حول یک محور

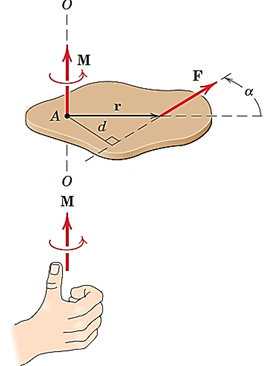
برای پیدا کردن گشتاور نیرو حول یک محور، کافیستگشتاور نیرو را حول یک نقطه از آن محور بدست آورده و سپس حاصل را در بردار یکه آن محور ضرب داخلی کرد. در شکل 12، بردار یکه راستای محورAB،λاست.

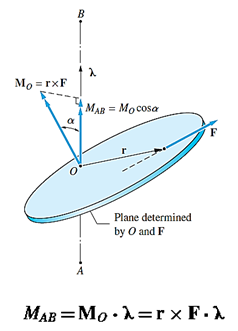
شکل 10- محاسبه گشتاور نیرویFحول محورAB

 

به صورت برداری می‌توان نوشت:

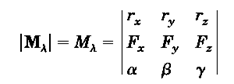
در این رابطه، β ،αوγمولفه‌های بردار یکه راستایAB هستند.

 

قضیه وارینیون

اگر به جسمی چندین نیرو مانندF₁،F₂ و .... وارد شود، مجموع گشتاورهای این نیروها حول نقطه ای مانندA برابر گشتاور برایند نیروها حول همان نقطه است (شکل 13).

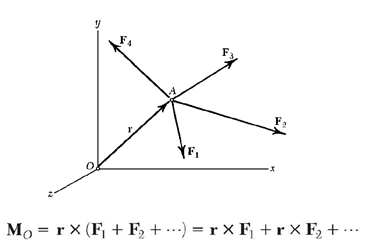
شکل 11- نمایش چند نیروی وارد شده به نقطهA برای بیان کاربرد قضیه وارینیون

کوپل

به گشتاور تولید شده توسط دو نیروی موازی، هم اندازه و خلاف جهت هم که بر یک خط قرار ندارند،کوپل گفته می‌شود. در حقیقت این دو نیرو تمایل به چرخش را در جسم ایجاد می‌کنند. اندازه گشتاور کوپل برابر حاصلضرب اندازه یکی از نیروها در فاصله عمودی بین خط اثر نیروهاست (شکل14).

کوپل‌ها در مکانیک جسم صلب، بردار آزاد هستند؛ بدین معنا که اثر آن‌ها برجسم صلب مستقل از نقطه اعمال آن‌هاست.

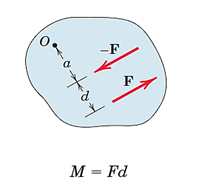
 شکل 12- نمایش دو نیروی وارد شده در صفحه که ایجاد گشتاور کوپل می‌کنند 

می‌توان بردار گشتاور کوپل را از حاصلضرب خارجی بردارr در بردارF پیدا کرد که این بردارها در شکل 16 نمایش داده شده اند

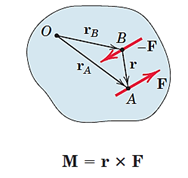
 شکل 13- نمایش گشتاور کوپل در صفحه 

کوپل‌های معادل

تا زمانی که حاصل ضربd درF تغییر نکند، تغییر دادن مقادیر آن‌ها باعث ایجاد تغییر در کوپل نمی‌شود. همچنینکوپل می‌تواند بدون تغییر تاثیر خارجی‌اش، در صفحه خود و یا در صفحات موازی آن جابجا شود. به این کوپل‌ها، کوپل‌های معادل گفته می‌شود (شکل 15).

 

 

 

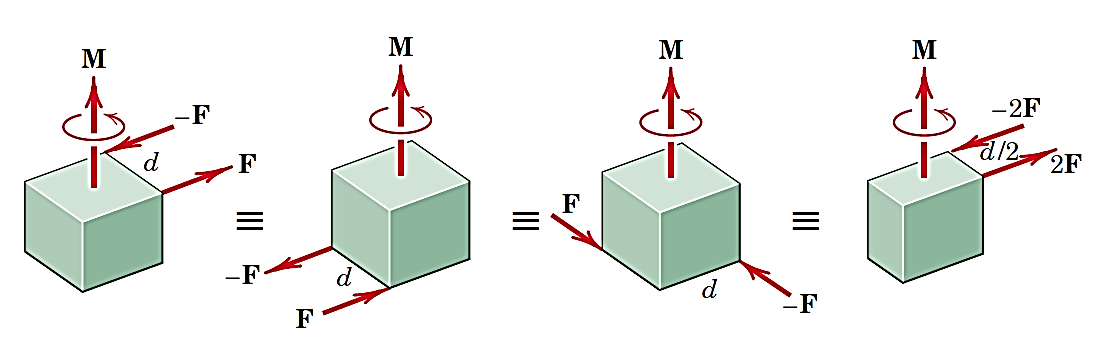
شکل14- نمایش کوپل‌های معادل

 

 

کوپل در فضا

برای محاسبه بردار کوپل در فضا، از قوانین مشابه کوپل صفحه ای استفاده می‌شود (شکل 17).

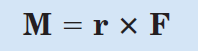
اندازه این کوپل برابر است با  

 

شکل 15-نمایش کوپل در فضا

سیستم کوپل- نیرو

نیروی وارد شده به جسم آن را کشیده یا هل می‌دهد، و یا حول هر محوری غیر از خط اثر خود نیرو، جسم را می‌چرخاند. این اثر دوگانه نیرو بر جسم را می‌توان با جایگزین کردن آن با یک نیروی موازی و یک کوپل بهتر نشان داد.

در فصل اول گفته شد که اگر نیروی وارد شده بر جسم صلب در راستای خط اثر خود جابجا شود، تاثیری که بر جسم می‌گذارد تغییر نمی‌کند. حال می‌خواهیم بررسی کنیم اگر نیرو در راستایی غیر از راستای خط اثر خود جابجا شود چه اتفاقی می‌افتد. به شکل 18 دقت کنید. همانطور که مشاهده می‌شود، با انتقال نیرویF به نقطهA، کوپلی برابرFd تولید می‌شود کهd فاصله عمودی بین دو راستا است. در مثال زیر، کوپل تولید شده پادساعتگرد است.

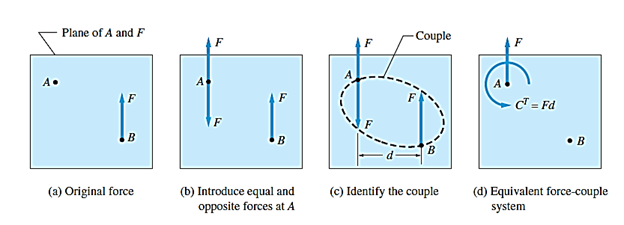
 شکل 16- نمایش جابجایی خط اثر نیرو 

بنابراین وقتی نیرو به راستایی غیر از راستای خط اثر خودش منتقل شود، در اثر این انتقال یک کوپل برای جبران تغییر گشتاور ایجاد می‌شود.

اغلب به سیستم‌ها نیروهای متفاوتی وارد می‌شود (شکل 19- تصویر چپ) که برای بررسی راحت‌تر سیستم، همه نیروها را به روش گفته شده یک نقطه خاص انتقال می‌دهیم. این نقطه می‌تواند مرکز جرم جسم و یا هر نقطه دیگری که در صورت سوال ذکر شده است باشد. دو سیستم نیرو زمانی با هم معادلند که بتوان آن‌ها را به یکسیستم نیرو- کوپل یکسان در یک نقطه معین مثلO تبدیل کرد. در شکل زیر، به جسم سه نیرو وارد شده است که با انتقال آنها به نقطهO، سه کوپل تولید می‌شود (شکل19- تصویر وسط). می‌توان برایند نیروها را با بردارR و برایند کوپل‌ها را با بردارM نمایش داد (شکل19-تصویر راست).

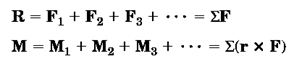
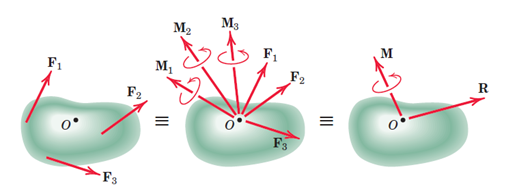
شکل17-نمایش یک  سیستم نیرو و سیستم نیرو- کوپل معادل آن در نقطهO

دقت شود مقدارR، یعنی نیروی برایند، مستقل از نقطه‌ای است که سیستم به آن انتقال داده می‌شود؛ اما مقدار و جهت کوپل برایندM به موقعیت این نقطه بستگی دارد.

رنچ

وقتی بردار ممان برایندM موازی بردار نیروی برایندR باشد، به این برایند رنچ گفته می‌شود. وقتی جهت بردارهایR وM یکسان باشد، رنچ مثبت (شکل 20- تصویر چپ) و در غیر اینصورت، رنچ منفی است (شکل 20- تصویر راست).

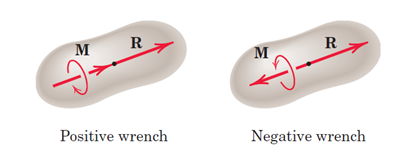
شکل18- نمایش رنچ مثبت (تصویر چپ) و منفی (تصویر راست)

رنچ ساده‌ترین فرم سیستم نیرو- کوپل است.

در شکل 21-a، حالت عمومی سیستم کوپل- نیروی معادل یک سیستم نیرو را مشاهده می‌کنیم کهR نیروی برایند  وM کوپل برایند است. با توجه به اینکهM یک بردار آزاد است، برای راحتی در نمایش سیستم، آن را به گونه‌ای قرار دادیم که از نقطهO بگذرد. حالM را در دو راستا تجزیه می‌کنیم؛ راستای بردارR (M₁) و راستای عمود بر آن(M₂) (شکل 21-b).می‌توان کوپلM₂ را با دو نیرویR و-Rبا فاصلهd= M₂/R جایگزین کرد (شکل 21-c). حال برایند نیرویR اولیه و نیروی-R صفر می‌شود. در نتیجه آنچه باقی می‌ماند، نیرویR در یک راستای جدید و کوپلM₁ است کهM₁نیز یک بردار آزاد است. بنابراین سیستم نیروی اولیه به یک رنچ مثبت تبدیل ش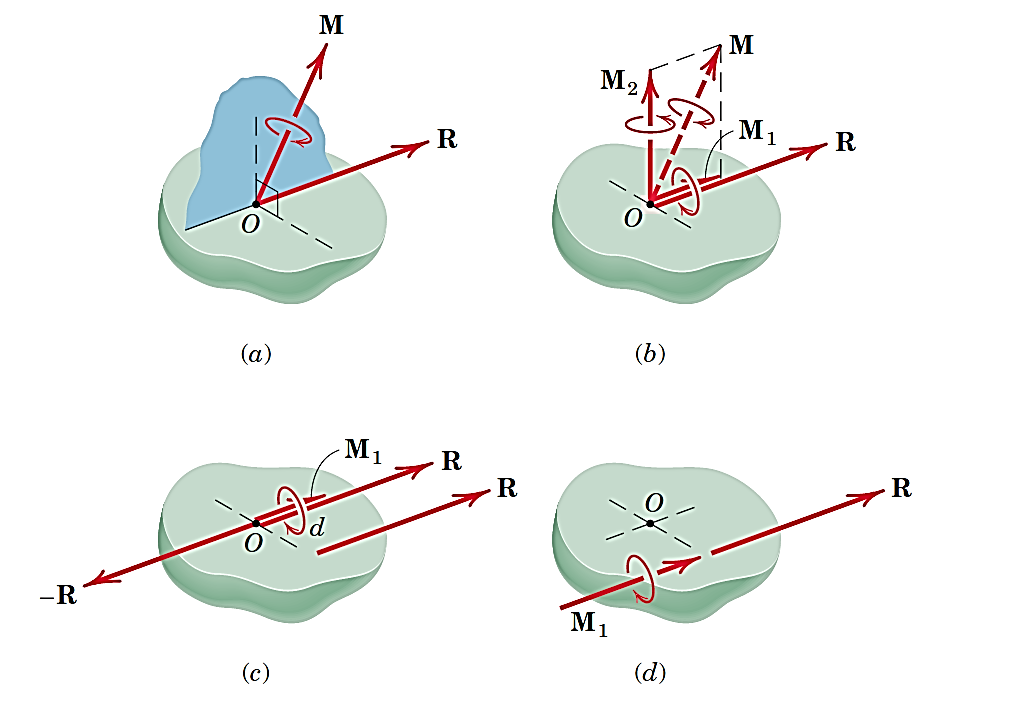

 شکل 19- تبدیل سیستم نیرو به یک رنچ 

---

برای تسلط بیشتر بر این مباحث، می‌توانید  کپسول آموزشی استاتیکلینوم را  مشاهده کنید.