فصل هشتم: ممان اینرسی

در آموزش قبلی دربارهکارهای مجازی در استاتیک صحبت کردیم و در این آموزش قصد داریم تا درموردممان اینرسی صحبت کنیم.

ممان اینرسی یاگشتاور دوم سطح، توزیع یک سطح را نسبت به یک محور یا یک نقطه نشان می‌دهد. به عبارت دیگر از بین دو شکل با سطح مقطع یکسان، شکلی که فاصله‌اش از یک محور بیشتر باشد، ممان اینرسی آن شکل نسبت به آن محور بیشتر است. در حقیقت ممان اینرسی نشان دهندهقدرت خمشی است؛ هرچه مقدار ممان اینرسی یک جسم نسبت به یک محور بیشتر باشد، خمش جسم حول آن محور سخت‌تر انجام می‌شود.

ممان اینرسی از روابط زیر محاسبه می‌شود (شکل 47):

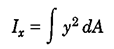
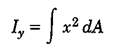
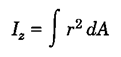
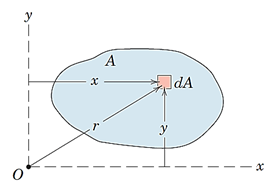
 شکل 45- درنظر گرفتن یک المان دیفرانسیلی برای محاسبه ممان اینرسی سطح 

بهI_xوI_y که توزیع سطح را نسبت به یک محور نشان می‌دهند ،ممان اینرسی مستطیلی و بهI_z که توزیع سطح را نسبت به یک نقطه نشان می‌دهد (مانند نقطهO در شکل 47)،ممان اینرسی قطبی گفته می‌شود.

رابطه بین این سه ممان اینرسی به صورت زیر است:

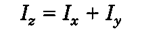
در جدول 3 که در انتهای مباحث قرار دارد، ممان اینرسی تعدادی از اشکال متداول را می‌بینیم.

قضیه محورهای موازی

به کمکقضیه محورهای موازی که به آن قضیه انتقال محورها هم گفته می‌شود، می‌توان ممان اینرسی یک سطح را نسبت به یک محور غیر مرکزی (محوری که از مرکز سطح عبور نمی‌کند)، بر حسب ممان اینرسی آن سطح نسبت به یک محور مرکزی و موازی بامحور غیر مرکزی بیان کرد (شکل 48).

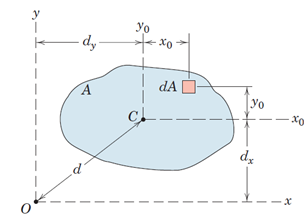
 شکل 46- قضیه محورهای موازی 

با توجه به شکل بالا برای محورx می‌توان نوشت:

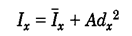
I̅_xممان اینرسی سطح نسبت به محور مرکزی (x₀در شکل 48)

I_xممان اینرسی سطح نسبت به محور غیر مرکزی (xدر شکل 48) و موازی با محورx₀

d_xفاصله بین دو محورx₀وx

مشابه همین رابطه را می‌توان برایI_yوI_z هم نوشت:

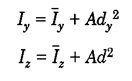
شعاع ژیراسیون (شعاع دوران)

شعاع ژیراسیونمفهوم فیزیکی بدیهی و مشخصی ندارد اما می‌توان آن را فاصله‌ای از یک محور مرجع دانست که اگر تمام سطح مورد نظر در آن فاصله متمرکز شود، ممان اینرسی بدست آمده حول محور برابر با ممان اینرسی سطح اولیه است. به عبارت دیگر، حاصلضرب مساحت در شعاع ژیراسیون به توان دو، همان ممان اینرسی خواهد بود:

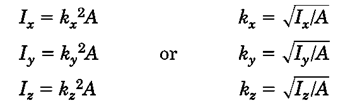
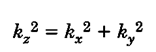
قضیه محورهای موازی برای شعاع ژیراسیون هم کاربرد داشته و به صورت زیر است:

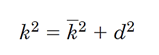
مشابه آنچه برای گشتاور اول سطح اجسام مرکب گفته شد، برای گشتاور دوم سطح اجسام مرکب حول یک محور خاص هم می‌توان از روابط زیر استفاده کرد:

 

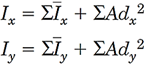
A مساحت هر یک از بخش‌ها

I ممان اینرسی شکل مرکب نسبت به محور مورد سوال

I̅ ممان اینرسی هر بخش نسبت به محور مرکزی خود آن بخش

d فاصله محور مرکزی هر بخش تا محور مورد سوال

جدول 3- مشخصات سطوح متداول

 

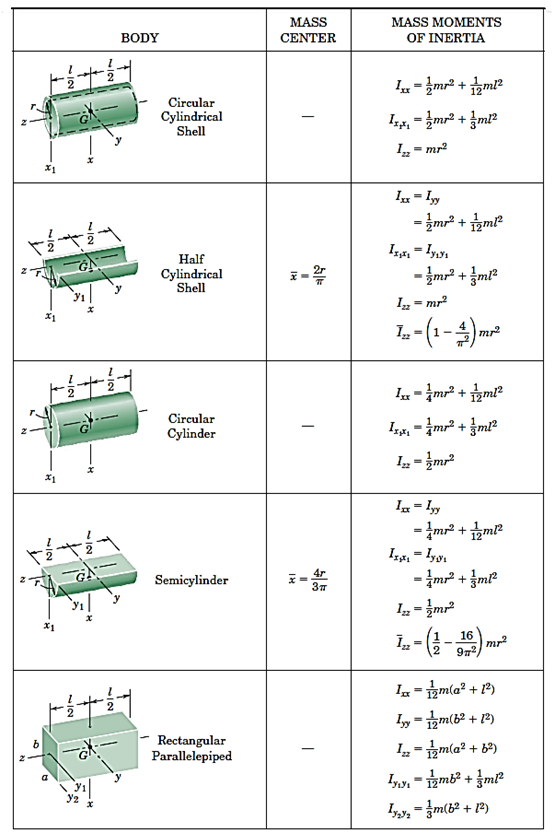
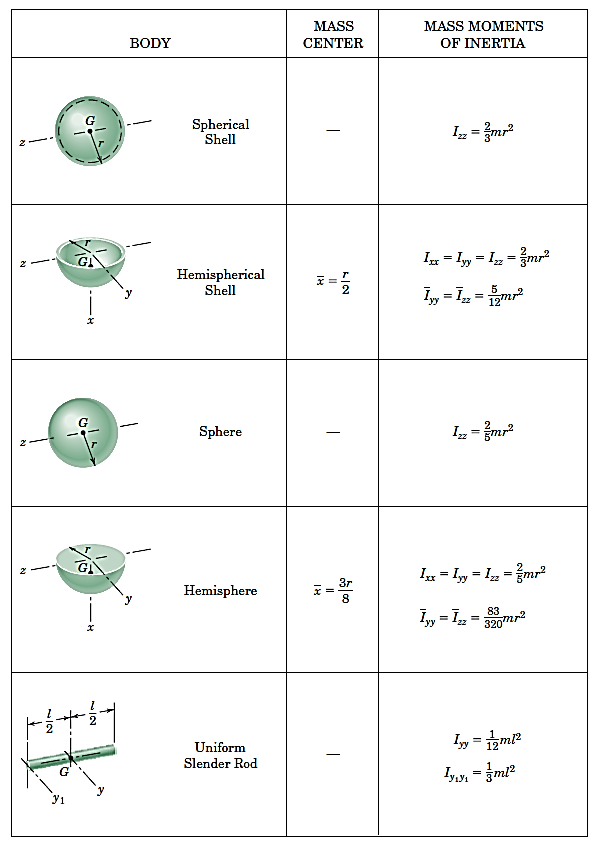
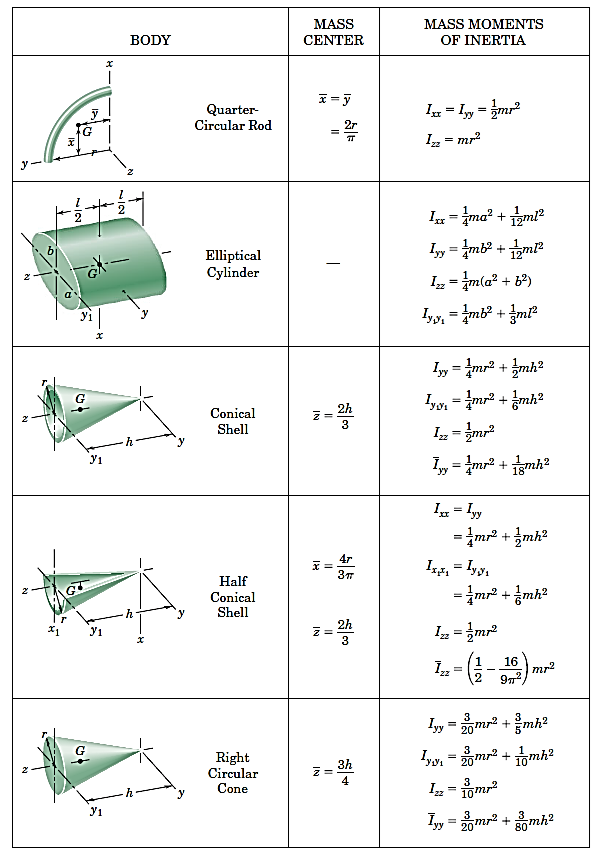
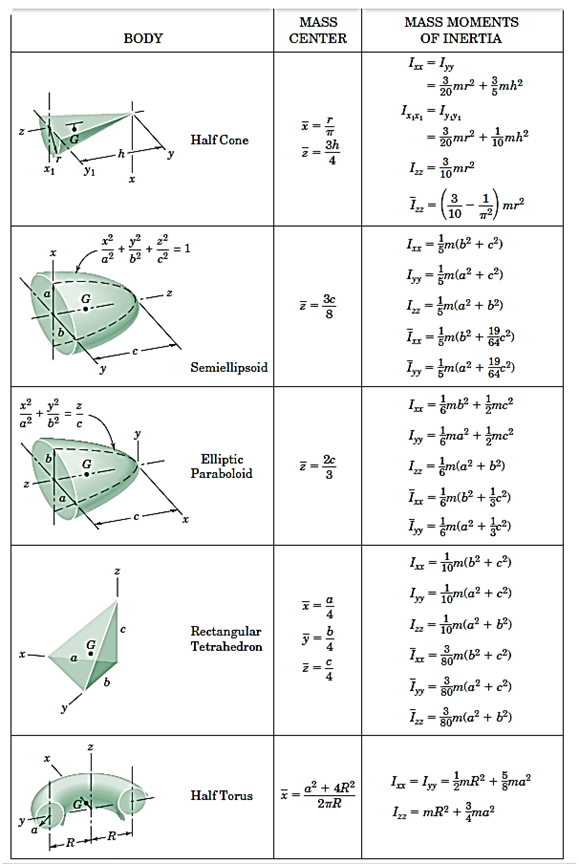
جدول4- مشخصات اجسام صلب یکنواخت متداول

---

برای تسلط بیشتر بر این مباحث، می‌توانید  کپسول آموزشی استاتیکلینوم را  مشاهده کنید.