فصل هفتم: کار مجازی

در آموزش قبلی در مورداصطکاک صحبت کردیم و در این آموزش قرار است در موردکارهای مجازی صحبت کنیم.

در ابتدا به بررسی مفهوم کار واقعی می‌پردازیم. کار واقعی، کمیتی اسکالر بوده و ناشی از یک جابجایی واقعی است.

کار نیرویF در جابجاییdr برابر است است با dU=F.dr= Fdscosα.

  dsاندازه بردار جابجایی وα زاویه بین بردار نیرو و جابجایی است.

کار گشتاورMهم در جابجایی به اندازهdθبرابر است باdU= Mdθ.

کار مجازی، کار ناشی از یک جابجایی مجازیست (ما فرض می‌کنیم که حرکت انجام شده در حالیکه در واقعیت اینطور نیست).

 روش تعادل نیروها مبتنی بر نیرو است که یک کمیت برداریست. به عبارتی هندسه مسئله در خود معادلات تعادل قرار دارد؛ در حالیکه در بسیاری از موارد، کار کردن با کمیت‌های اسکالر حل مسئله را برای ما راحت‌تر می‌کند. به همین دلیل در حل تعدادی از سوالات سراغ روش کار مجازی می‌رویم. در این روش، هندسه مسئله به صورت قید مجزا در حل مورد استفاده قرار می‌گیرد.

کار مجازی نیرویF در جابجاییrδبرابر است باU=F.δr= Fδscosαδ

کار مجازی گشتاورMهم در جابجایی مجازیδθبرابر است باδU= Mδθ.

اصل کار مجازی

اصل کار مجازی بیان می‌کند که مجموع کار مجازی انجام شده روی یک سیستم توسط تمام نیروهایActive در طول یک جابجایی مجازی برابر صفر است، به بیان ریاضی:U= 0δ

دقت شود کار نیروهایی مانند نیروهای داخلی و نیروهای تکیه‌گاهی در طول یک جابجایی مجازی برابر صفر است.

برای حل مسائل کار مجازی باید مراحل زیر را طی کرد:

1-رسم دستگاه مختصات

2-اعمال جابجایی مجازی در درجه آزادی مورد نظر

3-نوشتن اصل کار مجازی و قیدهای هندسی مسئله

4-حل معادلات

 

انرژی پتانسیل و تعادل

کار انجام شده روی یکجسم الاستیک به صورت انرژی پتانسیل الاستیک در آن ذخیره می‌شود؛ مانند کار انجام شده روی فنر الاستیک خطی که در یک جابجایی ازx₁ بهx₂ برابر هست با:

∆V_e= k (x₂²- x₁²)

این مقدار برابر است با مساحت زیر نمودار نیرو- جابجایی ازx₁ تاx₂.

اگرفنر پیچشی باشد، برای جابجایی به اندازهθ انرژی پتانسیل آن برابر می‌شود باV_e=12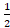 kθ².θ زاویه چرخش فنر بر حسب رادیان است.

 کار مجازی انجام شده روی یک فنر خطی در یک جابجایی مجازی به اندازهxδ  برابر است با:

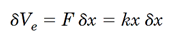
به همین ترتیب می‌توان کار مجازی انجام شده روی فنر پیچشی را نیز بدست آورد.

تغییر مجازی انرژی پتانسیل گرانشی برابر است با:

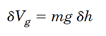
که در آنδh جابجایی مجازی مرکز جرم جسم به سمت بالاست.

معادله انرژی

 معادله انرژی به صورت زیر است:

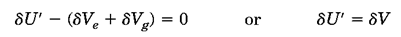
این رابطه بیان می‌کند که در تعادل، کل کار مجازی انجام شده روی سیستم توسط همه نیروهایActive (δU´) غیر از نیروی وزن و فنر، برابر است با کار مجازی انجام شده روی همان سیستم توسط نیروی فنر و وزن(δV_e+δV_g).

حال شرایطی را درنظر بگیرید که کار انجام شده روی سیستم توسط نیروهای غیرپتانسیل صفر باشد (δU´= 0). در این صورت معادله انرژی به صورتδV= 0در می‌آید. از نظر ریاضیاتی این حالت برابر است باdVdx=0 ؛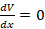

یعنی وقتی یک سیستم مکانیکی در تعادل باشد، مشتق انرژی پتانسیل آن برابر صفر است. دقت شود که در اینجا سیستم یک درجه آزادی است و این درجه آزادیx است.

تعادل (dVdx=0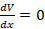) در سه موقعیت پیش می‌آید (شکل 46):

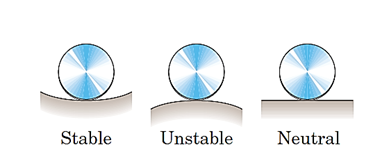
 شکل 44- نمایش سه حالت تعادل جسم 

تصویر چپ حالتی را نشان می‌دهد که دیسک در تعادل پایدار است؛ بدین معنی که با ایجاد اندکی جابجایی دیسک ازحالت تعادل، انرژی پتانسیل آن افزایش می‌یابد و تمایل دارد که به شرایط با انرژی پتانسیل کمتر برگردد. اما در تصویر وسط که دیسک در تعادل ناپایدار است، با ایجاد اندکی جابجایی،انرژی پتانسیل دیسک کاهش می‌یابد. در تصویر راست همتعادل خنثی را مشاهده می‌کنیم که در این حالت، در صورت ایجاد اندکی جابجایی در دیسک، سر جای جدید خود باقی می‌ماند.

برای تشخیص اینکهتعادل از نوع پایدار است یا غیر پایدار، باید مشتق دومV را نسبت به درجه آزادی سیستم (مثلاx) پیدا کنیم و از روی علامت عبارت حاصل، نوعتعادل مشخص می‌شود:

 

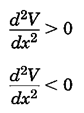
تعادل پایدار و تعادل ناپایدار

---

برای تسلط بیشتر بر این مباحث، می‌توانید  کپسول آموزشی استاتیکلینوم را  مشاهده کنید.