فصل پنجم: بارهای گسترده

در آموزش قبلی درموردسازه‌ها صحبت کردیم و در این آموزش هم قصد داریم تا درموردبارهای گسترده صحبت کنیم.

مفهوم مرکز ثقل، مرکز جرم و مرکز هندسی

جسمی را در نظر بگیرید که مانند شکل 27-a به کمک یک کابل از نقطهA آویزان شده است. به تمام ذرات این جسم نیروی وزن وارد می‌شود. برایند تمام این نیروها را باW نشان می‌دهیم. جسم تحت اثر دونیروی کشش کابل و نیروی وزن برایند، که در راستای نیروی کابل است، در حالت تعادل قرار دارد. خط اثر این نیروها را با یک خط فرضی مشخص می‌کنیم. جسم را از نقاطB وC آویزان کرده و همین کار را تکرار می‌کنیم (شکل 27-b وc). مشاهده می‌شود که تمام این خطوط یکدیگر را در نقطه‌ای قطع می‌کنند. این نقطه، که آن را باG مشخص می‌کنیم، مرکز ثقل جسم نام دارد.

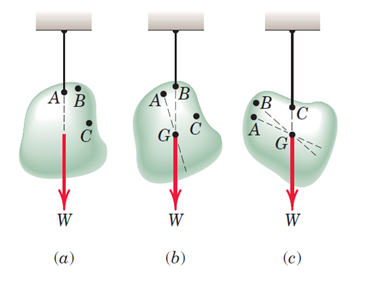
 شکل 25- جسم تحت اثر نیروی وزن و کشش کابل 

برای پیدا کردن مختصات مرکز ثقل اجسام از رابطه گشتاورها استفاده می‌شود (شکل 28).

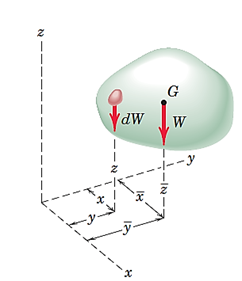
 شکل 26- پیدا کردن مختصات مرکز ثقل به کمک رابطه گشتاورها 

گشتاور نیروی وزن معادل (W) حول هر محوری، برابر است با مجموع گشتاورهای نیروی وزن وارد بر هر ذره (dw) حول همان محور است. به این ترتیب، مختصات مرکز ثقل جسم از روابط زیر محاسبه می‌شوند:

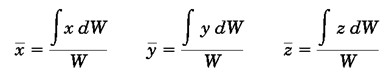
همانطور که مشاهده می‌شود، روابط بالا به شتاب گرانشg وابسته هستند. اگر در این رابطهW= mg وdw=gdmرا جایگذاری کرد، به روابط زیر می‌رسیم:

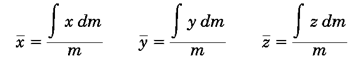
این روابط مستقل ازشتاب گرانش هستند. به عبارت دیگر، این روابط به ما مختصات نقطه‌ای را می‌دهند که تنها به نحوه توزیع جرم جسم وابسته است و نهمیدان گرانش. به این نقطه مرکز جرم جسم می‌گویند. اگر جسم در یکمیدان موازی و یکنواخت قرار داشته باشد، مرکز جرم و مرکز ثقل آن روی هم قرار دارند.

مرکز هندسی خط، سطح و حجم

خط: برای پیدا کردن مرکز هندسی خطوط، کافیست در رابطه بالاdm=ρAdl را با فرض ثابت بودنρ وA جایگذاری کنیم و پس از ساده کردن خواهیم داشت:

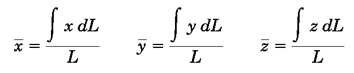
دقت شودمرکز هندسی خط لزوما روی خط قرار ندارد و ممکن است نقطه‌ای خارج آن باشد.

سطح: برای محاسبه مختصات مرکز سطوح،dm=ρtdA را با فرض ثابت بودنρ وt جایگذاری می‌کنیم:

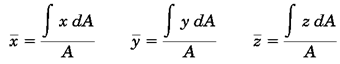
به صورت سه کسر بالا،گشتاور اول سطح گفته می‌شود.

حجم: کافیستdm=ρdvرا با فرض ثابت بودنρجایگذاری می‌کنیم و به رابطه زیر می‌رسیم:

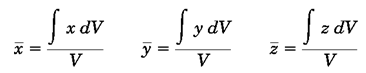
در صورت یکنواخت بودن دانسیته جسم، موقعیت مرکز هندسی و مرکز جرم یکی می‌شود.

محاسبه مرکز هندسی به روش انتگرال‌گیری

برای انتخاب المان مناسب در محاسبهمرکز هندسی اجسام به نکات زیر دقت شود:

1-مرتبه المان: تا حد امکان از المان دیفرانسیلی مرتبه یک استفاده می‌کنیم تا با یک انتگرال ساده بتوان کل شکل را پوشش داد. به طور مثال در شکل 29، به جای المان دیفرانسیلی نشان داده شده در شکل راست با مساحتdxdy، از یک المان مرتبه یک با ابعادldy (شکل چپ) استفاده می‌شود.

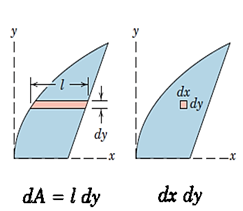
 شکل 27- المان دیفرانسیلی مرتبه اول (تصویر چپ) و مرتبه دوم (تصویر راست) 

2-پیوستگی: تا حد امکانالمال دیفرانسیلی را به گونه‌ای در نظر می‌گیریم که با یک عملیات پیوسته بتوان کل شکل را انتگرال‌گیری کرد. در شکل 30، اگر المان را مطابق تصویر راست به صورت عمودی درنظر بگیریم، درx=x₁دچار ناپیوستگی می‌شویم و بدین ترتیب به دو انتگرال برای پوشش دادن کل شکل نیاز است. چرا که ازx=0 تاx= x₁، المان بین محورx و منحنی بالا محصور است؛ اما ازx= x₁ به بعد، بین خط پایین و منحنی بالا محصور خواهد بود. اما در صورت انتخاب المان افقی، این ناپیوستگی ایجاد نخواهد شد و تنها به یکانتگرال احتیاج خواهد بود.

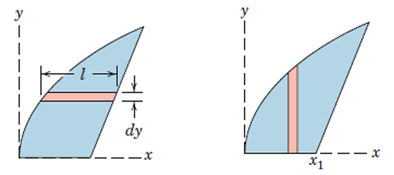
 شکل 28- مثالی از اهمیت پیوستگی در انتخاب المان دیفرانسیلی 

3- صرف نظر کردن از المان‌های با مرتبه بالاتر: در شکل 31، علاوه بر المان دیفرانسیلی مستطیلی با مساحتydx، یک المان دیفرانسیلی مثلثی کوچک در بالای المان مستطیلی با مساحتdxdy/2 نیز وجود دارد (المان پررنگ‌تر شکل) که از آن صرف نظر می‌شود. این مسئله خطایی ناچیزی در حل ایجاد می‌کند که قابل چشم پوشی است.

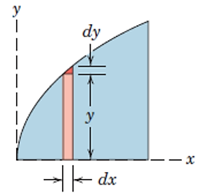
 شکل 29- می‌توان از المان با مرتبه بالاتر چشم پوشی کرد 

4- انتخاب دستگاه مختصات:دستگاه مختصاتی را انتخاب می‌کنیم که مرزهای شکل را به بهترین شکل توصیف کند. به همین دلیل در شکل 32، تصویرa را دستگاه دکارتی وb را در دستگاه قطبی تعریف می‌کنیم.

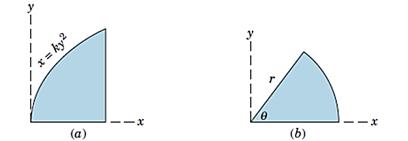
 شکل 30- انتخاب دستگاه مختصات مناسب 

5- در صورت انتخاب المان دیفرانسیلی مرتبه یک یا دو، از مختصات مرکز هندسی المان به عنوانبازوی گشتاور برای بیان گشتاور المان دیفرانسیلی استفاده می‌کنیم. به طور مثال در شکل 33 داریم:

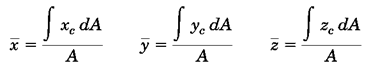
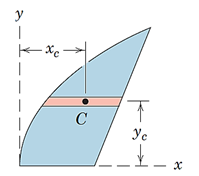
 شکل 31- استفاده از مختصات مرکز هندسی المان دیفرانسیلی برای بیان گشتاور المان 

در جدول شماره 3 در انتهای مباحث، مشخصات سطوح متداول مشاهده می‌شود.

مرکز جرم و مرکز هندسی اجسام مرکب

گاهی یک جسم را می‌توان به چند بخش تقسیم کرد که محاسبه مراکز جرم یامراکز هندسی آن بخش‌ها ساده‌تر است. در این صورت می‌توان مرکز جرم شکل کلی را از روابط زیر بدست آورد:

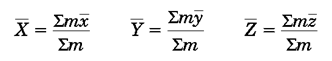
در این رابطهX̅،Y̅وZ̅مختصات مرکز جرم شکل کلی وx̅،y̅ وz̅  مختصات مرکز جرمقسمت‌هایی است که شکل کلی از آنها تشکیل شده است.m هم جرم هر یک از این بخش‌هاست.

به طور مشابه برای محاسبه مرکز سطح یک شکل مرکب داریم:

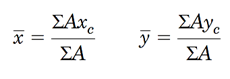
قضیه پاپوس

1)میله‌ای به طولL در اختیار داریم. اگر آن را حول محوری مانند xبه اندازهθدوران دهیم، رویه‌ای با مساحتA حاصل می‌شود که میتوان مساحت آن را به کمک رابطه زیر محاسبه کرد (شکل 34):

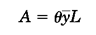
که در آنy̅،مختصهyمرکز هندسی میله است.

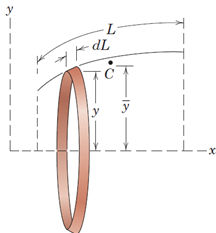
 شکل 32- رویه حاصل از دوران یک میله 

2) سطحی به مساحتA در اختیار داریم. چنانچه آن را حول محوری مانندx به اندازهθ دوران دهیم، حجمی برابر باV خواهیم داشت که این حجم را می‌توان از رابطه زیر پیدا کرد (شکل35):

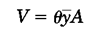
در این رابطه همy̅،مختصهyمرکز هندسی سطح است.

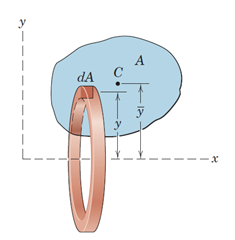
 شکل 33- حجم حاصل از دوران یک سطح 

بارهای گسترده بر تیرها- اثرات خارجی

در صورتی که به یک تیر بار گسترده وارد شده باشد، برای انجام محاسبات و پیدا کردن نیروهای تکیه‌گاهی تیر لازم است بار گسترده را با یک بار نقطه ای جایگزین کرد. اگر بار گسترده برابرw باشد، داریم (شکل 36):

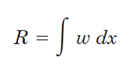
محل این بار نقطه‌ای روی مرکز هندسی بار گسترده است:

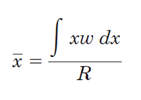
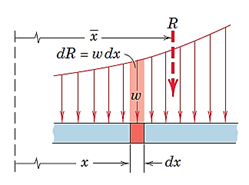
 شکل 34- جایگزینی بار گسترده با یک بار نقطه ای 

بارهای گسترده بر تیرها- اثرات داخلی

بارهای خارجی وارد بر تیرها باعث ایجاد نیروهای داخلی در تیر می‌شود. در این قسمت می‌خواهیم اثرات داخلی تیرها را بررسی کرده و با استفاده ازقوانین استاتیک، نیروی برشیV و ممان خمشی Mرا به صورت تابعی از موقعیت روی تیرx پیدا کنیم.

تغییراتنیروی برشی وممان خمشی در طول تیر از جمله اطلاعات مهم برای طراحی تیرها به شمار می‌روند. خصوصا ماکسیمم مقدار ممان خمشی و محل آن که از ملاحظات اولیه طراحی تیرهاست.

قدم اول برای پیدا کردن روابط نیروی برشی و ممان خمشی، تعیین مقادیر تمام نیروهای خارجی وارد بر تیر است. برای این کار باید دیاگرام جسم آزاد کل تیر رسم شده و معادلات تعادل آن نوشته و حل شوند. پس از آن، باید در تیر مقطعی بزنیم. اینکه سمت چپ مقطع بررسی شود یا سمت راست، بستگی به این دارد که معادلات تعادل کدام بخش راحت‌تر نوشته شود. دیاگرام جسم آزاد بخش انتخاب شده را رسم می‌کنیم و به کمک معادلات تعادل، عباراتی برایV وM آن قسمت از تیر بر حسبx بدست آوریم. برای جهتM وV تیر باید مطابق شکل 37 عمل کرد که در آن جهت مثبت این دو پارامتر نشان داده شده است:

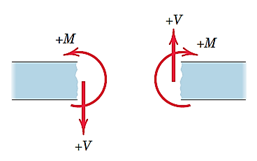
شکل 35- جهت مثبتM وV در تیر برش زده شده

در هر قسمت از تیر که رابطهM وV تغییر می‌کند، باید این مراحل را تکرار کرد. در مرحله آخر با توجه به روابط بدست آمده برای این دو پارامتر بر حسبx، نمودارهایM-xوV-xرسم و مقادیر ماکسیمم تعیین می‌شوند.

روابط میان بار، گشتاور خمشی و نیروی برشی

علاوه بر روش ذکر شده می‌توان به کمک روابطی که میان بار،گشتاور خمشی ونیروی برشی وجود دارد، روابط

M-x وV-xرا بدست آورد.

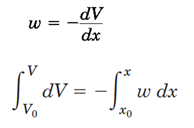
(منفی سطح زیر منحنی بار ازx₀تاx)V= V₀+  

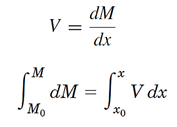
(منفی سطح زیر منحنی نیروی برشی ازx₀تاx)M= M₀+   

با استفاده از روابط بالا داریم:

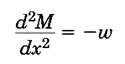
پیدا کردن نیروی داخلی اعضا

برای پیدا کردن نیروی داخلی اعضا در هر نقطه، ابتدا نیروهای تکیه‌گاهی لازم را با رسم دیاگرام جسم آزاد کل شکل و نوشتن معادلات تعادل بدست می‌آوریم. سپس در آن نقطه عضو را برش زده و دیاگرام جسم آزاد را برای قسمتی که معادلات راحت‌تری دارد، رسم می‌کنیم. در دیاگرام جسم آزاد باید نیروهای داخلی، یعنی نیروی برشی، ممان خمشی و نیروی عمودی، رسم شوند. سپس کافیست معادلات تعادل را نوشته و مجهولات را پیدا کنیم.

کابل‌های انعطاف پذیر

1-کابل‌های بدون وزن و حامل بار متمرکز

همانطور که شکل 38 مشاهده می‌شود، شکل این کابل‌ها به صورت خط صاف است.

 شکل 36- کابل بدون وزن با بار نقطه 

-کابل‌های بدون وزن و حاملبار گسترده یکنواخت در امتداد افق

همانطور که در شکل 39 دیده می‌شود، این کابل‌ها به سهمی درمی‌آیند. برای کابل‌های انعطاف پذیر به طور کلی معادله دیفرانسیل زیر را داریم:

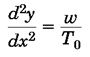
w بار گسترده وارد بر آن وT₀ کمترین کشش کابل است. حل این معادله به ماy= f(x) را می‌دهد که در حقیقت شکل کابل بوده وشرایط مرزی کابل (شرایط کابل در نقاط انتهایی) را ارضا می‌کند.

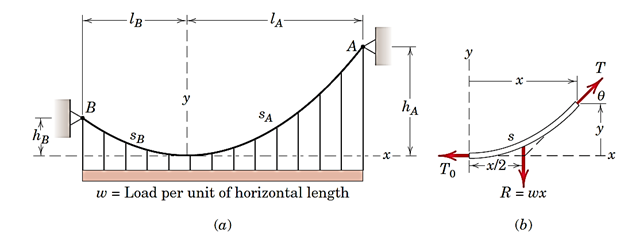
شکل 37-(a) کابل بدون وزن حامل بار گسترده. (b)دیاگرام جسم آزاد قسمت راست کابل

با یک بار دیگر انتگرال‌گیری به این رابطه می‌رسیم:

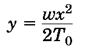
بیشترین مقدار تنش کابل (T_max) در جایی که شیب کابل حداکثر است (نقطهA در شکل 39) و کمترین مقدار آن(T₀) در جایی که شیب حداقل است (نقطهC) ایجاد می‌شود.

با توجه به معادلات تعادل در شکل 39-b میتوان نوشت:

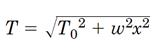
طول قسمت راست کابل (A تاC) را می‌توان از رابطه زیر پیدا کرد:

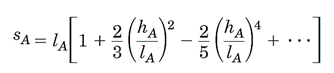
برای سمت چپ هم می‌توان مشابه همین رابطه را نوشت؛ با این تفاوت که بایدh_Bوl_Bرا در آن جایگذاری نمود.

3-کابل وزن‌دار یا زنجیری

 شکل این کابل به صورت تابع نمایی یاهیپربولیک است (شکل 40). قسمتی از کابل به طولs را در شکلbدر نظر گرفتیم و دیاگرام جسم آزاد آن را رسم کرده‌ایم. اگر وزن واحد طول کابلμ باشد، برایند نیروی وزن وارد شده بر قسمتی به طولs برابرμ sخواهد بود که آن را باR نمایش می‌دهیم.

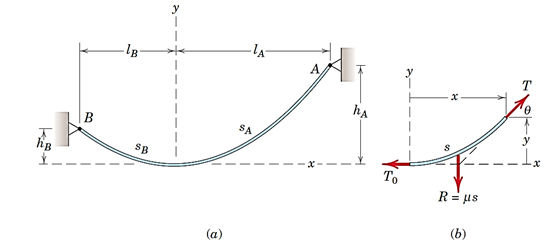
شکل 38- (a) کابل زنجیری. (b) دیاگرام جسم آزاد قسمت راست کابل

در نتیجه معادله دیفرانسیل کابل به صورت زیر است:

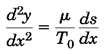
که با حل آن داریم:

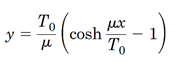
طول کابل را می‌توان به کمک رابطه زیر پیدا کرد:

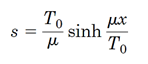
برای کشش کابل داریم:

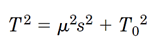
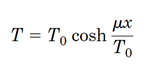
استاتیک سیالات

بررسیاستاتیک سیالات در حالت مایع را هیدرواستاتیک و در حالت گازیایرواستاتیکگویند. وقتی سیال حرکتی ندارد و ساکن است، تنش برشی که به باعث حرکت سیال می‌شود وجود ندارد؛ بنابراین در استاتیک سیالات فقط تنش عمودی وجود دارد که به آن فشار گفته می‌شود.

قانون پاسکال: فشار در هر نقطه از سیال در تمامی جهات یکسان است.

محاسبه فشار هیدرواستاتیک وارد بر صفحه تخت به شکل دلخواه غوطه‌ور در سیال

همانطور که در شکل 41 مشاهده می‌شود، یک صفحه تخت به شکل دلخواه داریم که با عمود زاویهθ می‌سازد و درسیال غوطه‌ور است. سطح بالایی سیال در صفحهx-y´قرار دارد.فشار سیال در همه جای سطح متناسب با عمق آن است به صورت عمود بر صفحه وارد می‌شود. می‌توان معادل نیروی سیال که به صورت گسترده بر صفحه وارد شده است، یک نیروی نقطه‌ای برایندR گذرنده از نقطهP قرار داد. حال می‌خواهیم مقدار این نیرو و محلP را پیدا کنیم.

برای این کار المان دیفرانسیلی نواری از سطح به مساحتdA درنظر می‌گیریم. نیروی وارد شده بر این المان دیفرانسیلیdR= PdA= ρghdA است کهP در تمام نقاط المان مقدار ثابتی است؛ چرا که در این المان نواری تغییر ارتفاع وجود ندارد. برای پیدا کردن کلنیروی وارد بر سطح کافیست ازdR انتگرال بگیریم:

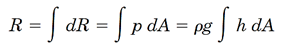
از آنجایی که داریم

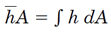
R به صورت روبرو درمی‌آید:

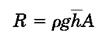
در حقیقتgh̅ρفشاری است که در عمق مرکز هندسی سطح، نقطهO، وجود دارد و میانگین فشار وارد بر این مساحت است.

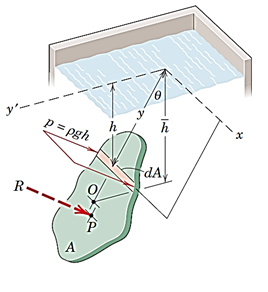
 شکل 39- فشار هیدرواستاتیک وارد بر صفحه تخت 

همانطور که گفته شد، فشار وارد شده بر هر نقطه از سطح عمود بر صفحه و متناسب با عمق آن نقطه است. در صورت رسم این فشار، شکل 42 بدست می‌آید. همانطور که مشاهده می‌شود، فشار عمودی و خود صفحه با هم تشکیل یک حجم می‌دهند. اندازه این حجم برابر نیرویR است و خط اثر آن از مرکز حجم این شکل (نقطهC) عبور می‌کند.

یک المان دیفرانسیلی حجمی در نظر می‌گیریم که سطح آن برابرxdy و ارتفاع آن برابرP=ρghاست. بنابراینdR= PdA= ρghxdyاست. برای محاسبه کل نیروی وارد بر سطح باید از این عبارت انتگرال گرفته شود:

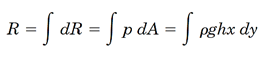
در رابطه بالا،h عمق المان دیفرانسیلی وx طول سطح آن است که باید برحسبy نوشته شود تا بتوان از رابطه انتگرال گرفت.

برای پیدا کردن محلR از قانون گشتاورها استفاده می‌شود:

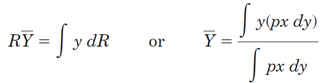
دقت شود که مرکز فشار و مرکز سطح صفحه (O) لزوما یک نقطه نیستند.

 شکل 40- حجمی که فشار عمود بر سطح و صفحه با هم می‌سازند 

محاسبه فشار هیدرواستاتیک وارد بر صفحه منحنی غوطه‌ور در سیال

 

محاسبه نیروی برایندR برای یک صفحه منحنی شکل غوطه‌ور در سیال محاسبات بیشتری نیاز دارد. یک روش نسبتا راحت‌تر این است که مطابق تصویر سمت راست در شکل 43، بلوکی از سیال را بالای صفحه درنظر بگیریم (بلوکABC). در اینصورتR در شکل، عکس العمل سطح در برابر نیروی سیال است؛ یعنی هم اندازه با آن و خلاف جهت آن است. برایند فشارها در طولAC وCB به ترتیب برابرP_yوP_xاست که به راحتی قابل محاسبه هستند. وزنW بلوک سیال از ضرب سطح مقطحABC در ضخامت ثابتb وρg بدست می‌آید. این نیرو از مرکز هندسی سطحABC می‌گذرد. بنابراین با رسمدیاگرام جسم آزاد این بلوک سیال و نوشتن معادلات تعادل می‌توانR را بدست آورد.

 

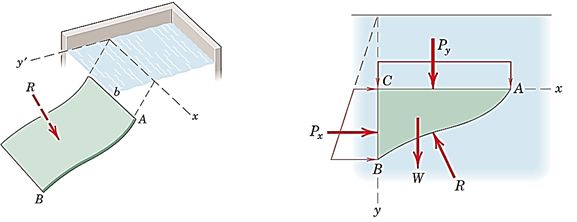
 شکل 41- فشار هیدرواستاتیک وارد بر صفحه منحنی 

نیروی شناوری

هر جسمی که در سیال قرار بگیرد، نیرویی رو به بالا به آن وارد می‌شود. به این نیرو،نیروی شناوری یابوینسی می‌گویند. منشا آن، افزایش فشار در سیال با افزایش عمق است. اندازه این نیرو برابر است باF=ρgV. در حقیقت این نیرو برابر است با وزن سیالی که حجم آن مساوی است با حجم جسم داخل سیال. جهت نیروی شناوری رو به بالا بوده و در مرکز حجم جابجا شده اثر می‌کند. اهمیت نیروی شناوری در طراحی و ساخت کشتی‌ها و زیردریایی هاست.

---

برای تسلط بیشتر بر این مباحث، می‌توانید  کپسول آموزشی استاتیکلینوم را  مشاهده کنید.