فصل چهارم: سازهها
در آموزش قبلی دربارهتعادل صحبت کردیم و در این آموزش قصد داریم درموردسازههاصحبت کنیم.
خرپا (تراس)
.خرپا یاتراس از عضوهایی تشکیل شده است که در دو انتها (مفصل) به هم متصل هستند. خرپا میتواند صفحهای یا فضایی باشد. جزء اصلی خرپای صفحهای به شکل مثلث است. در شکل 24 نمونههایی از خرپاهای متداول در ساخت پلها و سقفها را میبینیم
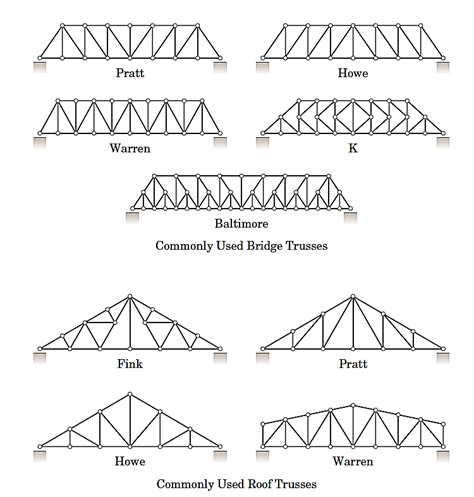
شکل 22- نمونههایی از خرپاهای متداول در پلها و سقفها
برای تحلیل خرپاها آنها را عضوهایی دو نیرویی درنظر میگیریم که فشار یا کشش تحمل میکنند. (مطابق شکل 25)
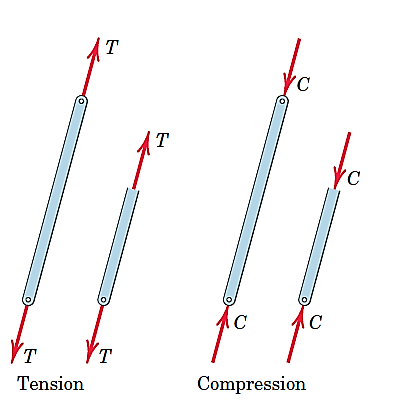
شکل 23- خرپاها اعضای دونیرویی هستند و کشش یا فشار را تحمل میکنند.
معمولا در مسائل از وزن خرپاها صرف نظر میشود اما اگر در مسئلهای این وزن قابل صرف نظر نباشد، باید آن را نصف کرده و روی هر مفصل خرپا، نصف وزن را قرار دهیم.
خرپای صفحهای
اگرm را تعداد عضوهای خرپا وj را تعداد مفاصل آن درنظر بگیریم، خرپای صفحهای ممکن است یکی از سه حالت زیر را داشته باشد:
1-اگر خرپا معین استاتیکی داخلی باشد، بین تعداد عضوها و مفاصل رابطهm+ 3 = 2j برقرار است. این شرط لازم برای پایداری خرپاست ولی شرط کافی نیست؛ چون ممکن است خرپا طوری آرایش یافته باشد که پایدار نباشد.
2- اگر m+ 3 > 2jباشد، خرپا نامعین استاتیکی داخلی است.
3-اگرm+ 3 < 2j باشد، خرپا ناپایدار بوده و تحت بارگذاری فرو میریزد.
در حل مسائل خرپا، هدف پیدا کردن نیروهای تکیهگاهی و نیروهای داخلی اعضاست. برای این کار دو روش وجود دارد؛ روش مفصلها و روش مقاطع. در ادامه هرکدام از این روشها توضیح داده میشوند.
روش مفصلها
در این روش ابتدادیاگرام جسم آزاد کل خرپا را رسم کرده و به کمک معادلات تعادل، نیروهای تکیهگاهی محاسبه میشوند. سپس حل از مفصلی که حداقل یک نیروی معلوم و حداکثر دو نیروی مجهول دارد شروع میشود.
نیروهای وارد بر مفصل رسم شده و سپس معادلات تعادل نوشته میشوند (برای هر مفصل دو معادله تعادل نیرو).
اثر عضوهای متصل به مفصل به صورت نیروی خارجی درنظر گرفته میشوند.
با حل معادلات تعادل، نیروهای مجهول اعضای متصل به آن مفصل پیدا میشوند.
همین مراحل را برای مفاصل بعدی انجام میدهیم تا نیروهای داخلی تمام اعضا پیدا شوند.
مشابه آنچه در فصل پیش درباره جهتنیروهای تکیهگاهی گفته شد، در اینجا هم برای نیروی داخلی اعضا یک جهت فرض کرده (کشش یا فشار) و مسئله را حل میکنیم. در صورت مثبت شدن جواب بدست آمده، جهت فرض شده درست است و در غیر اینصورت، جهت واقعی برعکس آن چیزی است که فرض شده بود.
روش مقاطع
این روش معمولا در سوالاتی کاربرد دارد که نیروهای داخلی تمام اعضا مورد سوال نباشد؛ بلکه نیروی اعضای خاصی خواسته شده باشد که بتوان با زدن مقطع مناسب، آنها را پیدا کرد.
خط برش از عضو عبور میکند و نه مفاصل.
در این روش، علاوه بر معادله تعادل نیروها، از تعادل گشتاور هم استفاده میشود. به دو نکته درباره تعیین مرکز گشتاور باید توجه شود. اول آنکه مرکز گشتاور به گونهای انتخاب میشود که تعداد نیروی مجهول بیشتری از آن عبور کند. دوم آنکه مرکز گشتاور ممکن است روی مقطع مورد بررسی و یا حتی خارج از آن باشد.
باید دقت شود که مقطع انتخابی بیش از سه نیروی مجهول نداشته باشد.
بعد از مقطع زدن، میتوان هر یک از دو قسمتخرپا را بررسی نمود. ترجیح آن قسمتی است که سادهتر باشد.
لزومی ندارد در حل سوالات تنها از یکی از دو روش ذکر شده استفاده کرد؛ بلکه میتوان از هر دو برای حل سوال و پیدا کردن نیروهای مجهول استفاده کرد.
خرپای فضایی
اگر مانند خرپای صفحهای، در خرپای فضایی هم mرا تعداد عضوها وj را تعداد مفاصل درنظر بگیریم، خرپای فضایی ممکن است یکی از سه حالت زیر را داشته باشد:
1-اگر خرپا معین استاتیکی داخلی باشد، بین تعداد عضوها و مفاصل رابطهm+ 6 = 3j برقرار است. این شرط لازم برای پایداری خرپاست.
2- اگر m+ 6 > 3jباشد، خرپا نامعین استاتیکی داخلی است.
3-اگرm+ 6 < 3j باشد، خرپا ناپایدار بوده و تحت بارگذاری فرو میریزد.
دو روش مقاطع و مفصلها برای خرپای فضایی هم استفاده میشود. در روش مفصلها، برای هر مفصل باید نوشت:
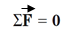
بنابراین در روش مفصلها برای خرپای فضایی، برای هر مفصل سه معادله تعادل میتوان نوشت. به همین دلیل مفصل انتخابی برای شروع تحلیل باید حداکثر سه نیروی مجهول و حداقل یک نیروی معلوم داشته باشد.
در روش مقاطع هم برای هر مقطع باید نوشت:
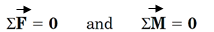
پس در این روش برای خرپای فضایی، 6 معادله تعادل میتوان نوشت. بنابراین، مقطع انتخابی نباید بیش از 6 نیروی مجهول داشته باشد.
قاب و ماشین
قاب و ماشین سازههایی هستند که حداقل یک عضو چند نیرویی دارند. قاب برای تحمل بارهای خارجی طراحی و ساخته میشود و در جای خود ثابت است؛ اما ماشین دارای بخشهایی محرک است و نیروها یاکوپلهای ورودی را به نیروها یا کوپلهای خروجی تبدیل میکند.
به این نکته دقت شود که لزوما همه اعضای قاب و ماشین چند نیرویی نیستند و مکن استاعضایی دونیرویی هم در آنها وجود داشته باشد.
ممکن است در یک قاب یا ماشین، تعداد عضوهای سازه یا تعداد تکیهگاهها از تعداد لازم برای حفظ پایداری سازه بیشتر باشد که در این صورت میگوییم مسئله از نظر استاتیکی نامعین است. در این صورت با نوشتن معادلات تعادل استاتیکی نمیتوان نیروهای تکیهگاهی را پیدا کرد.
اگر قاب یا ماشین صلب باشد؛ یعنی پس از جدا شدن از تکیهگاههایش فرو نریزد (شکل26-a)، برای حل ابتدا دیاگرام جسم آزاد کل سازه را رسم میکنیم و با کمک معادلات تعادل، نیروهای تکیهگاهی محاسبه میشوند. سپس برای پیدا کردن نیروهای اعضا لازم است که سازه تجزیه و روابط تعادل برای هر عضو نوشته شود.
در صورتیکه قاب یا ماشین غیرصلب باشد (شکل26-b)، سازه با جدا شدن از تکیهگاهها فرو میریزد و با رسم دیاگرام جسم آزاد کل سازه نمیتوان نیروهای تکیهگاهی را یافت؛ چرا که تعداد مجهولات از معادلات بیشتر است. به همین دلیل بایدسازه را از ابتدا تجزیه کرد.
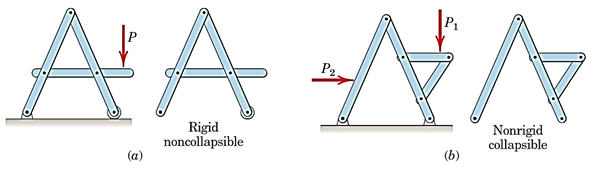
شکل 24-(a) سازه صلب . (b) سازه غیر صلب
برای تسلط بیشتر بر این مباحث، میتوانید کپسول آموزشی استاتیکلینوم را مشاهده کنید.