فصل سوم: تعادل
در آموزش قبل درباره سیستمهای نیرو صحبت کردیم. در این آموزش قصد داریم درموردتعادل در استاتیک صحبت میکنیم.
شرط لازم و کافی برای اینکه جسمی در تعادل باشد این است که برایند نیروها و برایند گشتاورهای وارد بر آن صفر باشد؛ یعنی
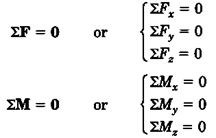
بنابراین در حالت کلی برای تعادل یکجسم صلب در فضا 6 معادله وجود دارد؛ اما بسته به اینکه مسئله در صفحه تعریف شده است یا فضا و نیز با توجه به شرایط نیروها، تعداد این معادلات میتواند کمتر شود.
قدم اول در حل مسائل تعادل، رسم دیاگرام جسم آزاد است. برای استفاده از قوانین مکانیک در تحلیل نیروهای وارد بر جسم، باید آن جسم را از بقیه اجسام جدا کرده و دیاگرام کاملی از تمام نیروهای وارد بر آن، از جمله نیروهای خارجی و تکیهگاهی، رسم کرد. به این دیاگرام، دیاگرام جسم آزاد گفته میشود. در صورت نادرست کشیدن دیاگرام جسم آزاد، ادامه حل نیز نادرست خواهد بود؛ بنابراین در رسم آن باید دقت کافی داشت.
در ادامه با انواع اتصالات و تکیهگاههای مسائل دوبعدی آشنا میشویم تا از این اطلاعات دررسم دیاگرام جسم آزاد استفاده کنیم.

کابل، طناب یا زنجیر بدون وزن(شکل بالا) و وزندار (شکل پایین)

سطح بدون اصطکاک: نیروی عمودی سطح
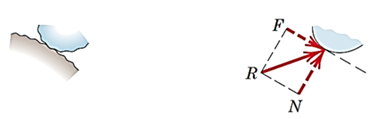
سطح با اصطکاک: نیروی عمودی سطح و اصطکاک
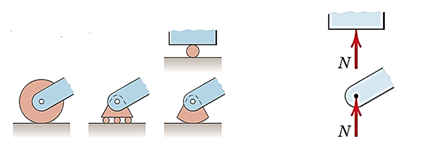
تکیهگاه غلتکی
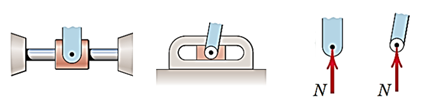
تکیهگاه ریلی
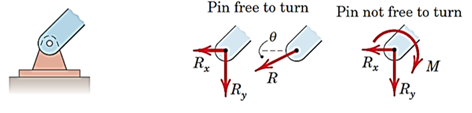
تکیهگاه پین (شکل وسط: پین با قابلیت چرخش- شکل راست: پین بدون چرخش)
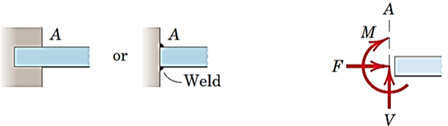
تکیهگاه گیردار
جدول1- اتصالات و تکیهگاههای دوبعدی
پس از رسم دیاگرام جسم آزاد، باید معادلات تعادل مورد نیاز نوشته شوند. در شکل 22 چهار حالتی که برای نیروهای وارد بر جسم در صفحه ایجاد میشود و نیز معادلات تعادل مورد نیاز هر حالت مشاهده میشود.تصویرa
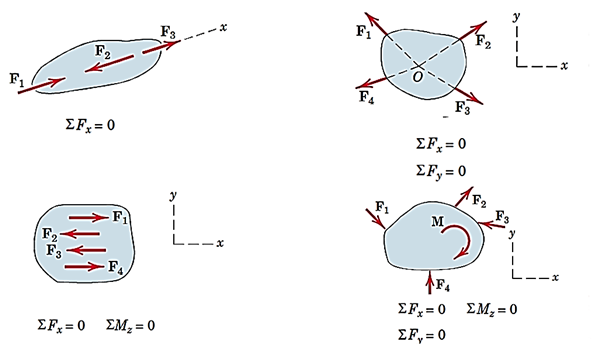
شکل20- معادلات تعادل برای جسم در دوبعد در چهار حالت مختلف نیروها
از شکل 22 حالتی را نشان میدهد که نیروهای وارد بر جسم همراستا باشند. در این صورت برای تعادل کافیست برایند نیروها در همان راستا برابر صفر باشد.
در تصویرb نیروها در یک نقطه همرس هستند؛ مانند نیروهای وارد بر ذره در صفحه. در این صورت برای تعادل با توجه به شکل، برایند نیروها در دو راستایx وy باید صفر باشد.
اگر نیروها موازی باشند، مانند تصویرc، برایند نیروها در راستای نیروها و نیز گشتاور آنها حول محور عمود بر صفحه باید صفر شود تا جسم در تعادل باشد.
تصویرd، حالت کلی جسم صلب در صفحه را نشان میدهد. در این شرایط باید برایند نیروها در دو راستایx وy و برایند گشتاورها حول محور عمود بر صفحه، یعنی محورz، صفر باشد.
تعادل در سه بعد
مشابه حالت دو بعدی، ابتداانواع اتصالات و تکیهگاههای سه بعدی را بررسی میکنیم.
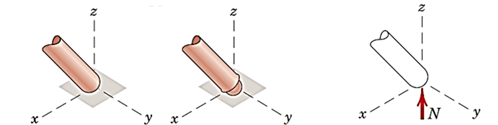
تکیهگاه کروی بدون اصطکاک
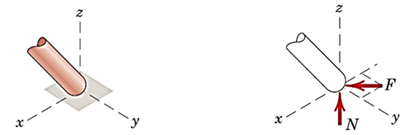
تکیهگاه کروی با اصطکاک
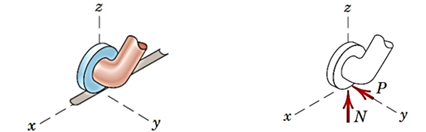
تکیهگاه غلتکی
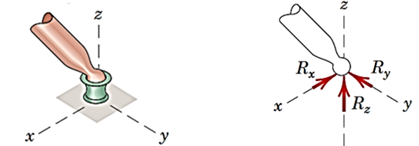
تکیهگاه گوی و کاسه

تکیهگاه ثابت
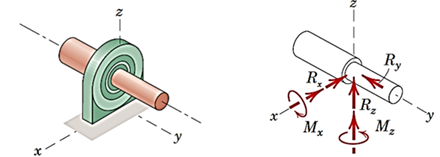
یاتاقان (در شکل، یاتاقان بار محوری تحمل میکند؛ به همین دلیل در دیاگرام آنRy داریم. اگر یاتاقان بار محوری تحمل نکند، یعنی در راستای محور خود بتواند حرکت کند، در راستای محور نیرویی نخواهیم داشت)
جدول2- انواع اتصالات و تکیهگاههای سه بعدی
در هردو مسائل دو و سه بعدی، در صورتی که جهت درستنیروی تکیهگاهیمشخص نباشد، جهت دلخواهی برای آن درنظر گرفته و مسئله را حل میکنیم. درصورت مثبت شدن جواب نهایی، جهت درنظر گرفته شده درست بوده و درغیر اینصورت، جهت واقعی خلاف جهت درنظر گرفته شده است.
در شکل 23 حالتهایی که برای نیروهای وارد بر جسم در فضا ایجاد میشود و نیز معادلات تعادل مورد نیاز هر حالت مشاهده میشود. در شکلa نیروها در یک نقطه همرس هستند؛ مانند تعادل ذره در فضا. تصویرb حالتی را نشان میدهد که نیروها به یک خط همرس هستند. همانطور که مشاهده میشود، از 6 معادله حالت کلی، در اینجا 5 معادله نیاز است و معادله ششم خود به خود ارضا میشود. برای تصویرc که در آننیروها موازی هستند، برایند نیروها در راستای توازی و برایند گشتاورها حول دو محور دیگر باید صفر باشد. در حالت کلی که در شکلd نشان داده شده است، نوشتن هر 6 معادله تعادل جسم صلب در فضا نیاز است.
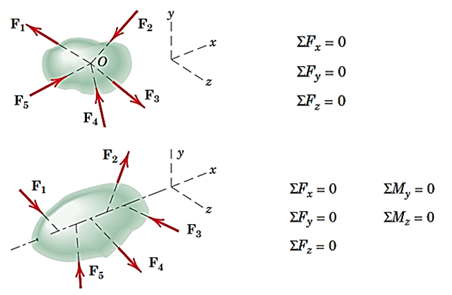
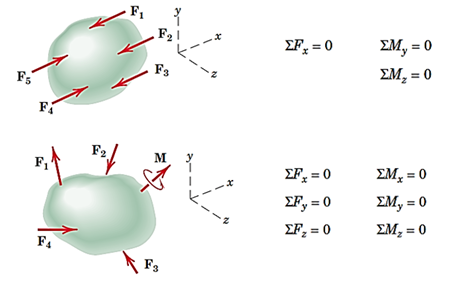
شکل21- معادلات تعادل برای جسم در فضا در چهار حالت مختلف نیروها
برای تسلط بیشتر بر این مباحث، میتوانید کپسول آموزشی استاتیکلینوم را مشاهده کنید.