انتگرال‌های ناسره

در اینآموزش کپسولی لینوم، به سراغ یادگیریانتگرال‌های ناسره و قضایای مختلف می‌رویم.

صورت های مبهم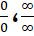   

قضیه کوشی شوارتز

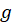اگر توابع و در بازه بسته  پیوسته و در فاصله باز مشتق‌پذیر باشند و اگر به ازای همه مقادیر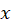 در بازه‌ی 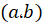، 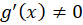آنگاه حداقل یک عدد همانند 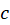در بازه‌ی 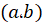وجود دارد به طوری که:

دستورهوپیتال

اگر توابع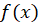 و مشتق‌پذیر باشند و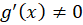 باشد, در صورتی که جواب حد 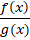به صورت مبهم درآید، در این صورت می‌توان از قاعده هوپیتال استفاده کرد.

قاعده هوپیتال به این صورت است که از صورت و مخرج به صورت جداگانه مشتق گرفته و سپس حد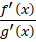 را بررسی خواهیم‌کرد.

برخی صورت های مبهم مهم

علاوه بر موارد نام‌برده شده، صورت‌های مبهم دیگری نیز وجود دارند که به صورت موارد زیر هستند:

دراین‌گونه مسائل، با روش‌های مناسب سعی می‌کنیم تا به یکی از حالت‌های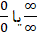 تبدیل کرده و از روش هوپیتال یا روش‌های دیگر استفاده خواهیم‌کرد.

انتگرال‌های ناسره

اگر تابع در بازه‌ی  پیوسته و نامنفی باشد، مساحت ناحیه بین منحنی 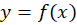 و محور 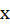ها در بازه‌ی 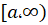 برابر است با :

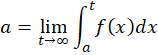
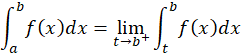
اگر تابع به ازای اعدادی چون در بازه‌ی بازدارای ناپیوستگی نامتناهی بوده ولی در بازه‌ی نقاط  پیوسته باشد، در این صورت تعریف می‌کنیم که:

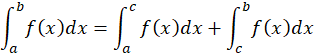
انتگرال های ناسره با انتگرال بی‌کران

اگر تابع در بازه‌ی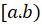  پیوسته باشد و باشد، در این صورت خواهیم‌داشت:

اگر حد فوق وجود داشته باشد،انتگرال ناسره‌ی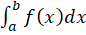 را همگرا و درغیر اینصورت آن را واگرا گویند.

اگر در بازه‌ی پیوسته و باشد, در این صورت خواهیم‌داشت:

اگر تابع به ازای اعدادی چون در بازه‌ی باز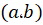 دارایناپیوستگی نامتناهی بوده ولی در بازه‌ی نقاط  پیوسته باشد، در این صورت تعریف می‌کنیم که:

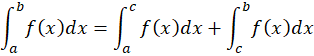
*انتگرال ناسره تنها وقتی همگرا است که هر دو انتگرال طرف راست همگرا باشند.

فرمول تیلور

قضیه: اگر یک تابع باشد به طوری که مشتق‌های اول تا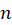 ام آن در  وجود داشته‌باشند، در این صورت چند جمله‌ای زیر را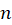 امین چندجمله‌ای حول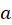 می‌نامیم.

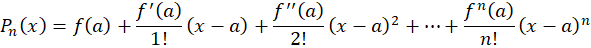
*نکته: اگر را در فرمول قرار دهیم،قضیه تیلور بهقضیه مک لورن تبدیل می‌شود.

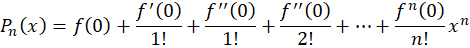
قضیه تیلور

اگر یک تابع و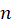 عددی طبیعی باشد به طوری که: 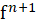در بازه‌ی 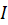وجود داشته باشد، اگر و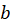 دو عدد متفاوت در 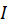باشند، آنگاه عددی چون 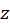وجود دارد به طوری که:

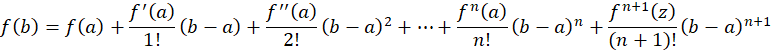
به ازای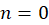، فرمول بالا به صورت 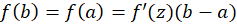تبدیل می‌شود.

برای تسلط بیشتر بر این مباحث، می‌توانید کپسول آموزش ریاضی عمومی2 لینوم را هم مشاهده کنید.