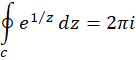5) معرفی دنباله ها و سری های مختلط و روش حل سری های مختلط

1-5 دنباله های مختلط
در اینآموزش کپسولی لینوم، به سراغ یادگیری دنبالههای مختلط میرویم.
دنباله نامتناهی 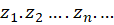 در اعدادمختلط دارای حد
در اعدادمختلط دارای حد 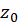 است اگر
است اگر
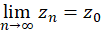
در این صورت گوییم که دنباله 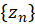 به
به همگرا است. میتوان نشان داد که حد یک دنباله در صورت وجود منحصربهفرد است. اگر یک دنباله دارای حد نباشد، آن را واگرا مینامیم.
همگرا است. میتوان نشان داد که حد یک دنباله در صورت وجود منحصربهفرد است. اگر یک دنباله دارای حد نباشد، آن را واگرا مینامیم.
قضیه زیر حد دنباله های مختلط را به حد دنبالههای حقیقی مربوط میسازد.
قضیه1: دنباله 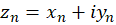 دارای حد
دارای حد 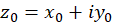 است اگر و فقط اگر دنباله های حقیقی
است اگر و فقط اگر دنباله های حقیقی 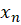 و
و 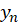 به
به 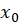 و
و 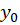 همگرا باشند.
همگرا باشند.
 مثال1 )چون دنباله های حقیقی
مثال1 )چون دنباله های حقیقی 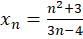 و
و 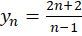 ، به ترتیب به
، به ترتیب به  و
و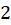 همگرا هستند، پس دنباله مختلط
همگرا هستند، پس دنباله مختلط 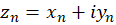 به
به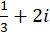 همگرا است.
همگرا است.
2-5 سری های عددی مختلط
اگر 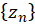 یک دنباله مختلط باشد، حاصل جمع جملات آن را به شکل
یک دنباله مختلط باشد، حاصل جمع جملات آن را به شکل 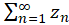 نمایش داده و آن را یکسری مختلط مینامیم. سری راهمگرابه عدد
نمایش داده و آن را یکسری مختلط مینامیم. سری راهمگرابه عدد 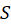 نامیم اگر دنباله
نامیم اگر دنباله 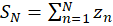 ،
،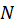 اُمینحاصل جمع جزئی، به
اُمینحاصل جمع جزئی، به 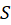 همگرا گردد، یعنی
همگرا گردد، یعنی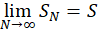 در اینصورت مینویسیم:
در اینصورت مینویسیم:
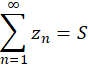
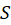 رامقدار سریمینامند.
رامقدار سریمینامند.
توجه کنید که چون حد یک دنباله در صورت وجود منحصربه فرد است، بنابراین حد دنباله 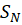 یعنی مقدارسری نیز درصورت وجود منحصربهفرد می گردد. اگر یک سری همگرا نباشد، آن راواگرامینامیم.
یعنی مقدارسری نیز درصورت وجود منحصربهفرد می گردد. اگر یک سری همگرا نباشد، آن راواگرامینامیم.
قضیه زیر مقدار یک سری مختلط را به مقدار سریهای حقیقی مربوط میکند.
قضیه2: سری 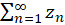 ، که در آن
، که در آن 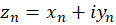 به مقدار
به مقدار 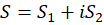 همگرا هستند، همگراست اگر و فقط اگر سریهای حقیقی
همگرا هستند، همگراست اگر و فقط اگر سریهای حقیقی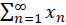 و
و 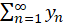 به ترتیب به
به ترتیب به 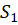 و
و 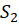 همگرا گردند.
همگرا گردند.
 مثال2 )چون سریهای حقیقی
مثال2 )چون سریهای حقیقی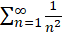 و
و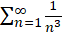 همگرا هستند، پس سری مختلط
همگرا هستند، پس سری مختلط 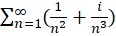 نیز همگراست.
نیز همگراست.
 مثال3 )سری
مثال3 )سری 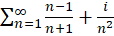 یک سری واگراست زیرا فاقد شرط لازم همگرایی است.
یک سری واگراست زیرا فاقد شرط لازم همگرایی است.
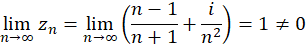
اگر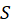 مقدار سری
مقدار سری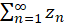 باشد،
باشد، 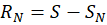 راباقیماندهسری مینامند. توجه کنید که چون
راباقیماندهسری مینامند. توجه کنید که چون 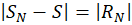 ، بنابراین اگر سری همگرا باشد، یعنی
، بنابراین اگر سری همگرا باشد، یعنی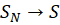 ، آنگاه
، آنگاه 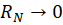 .
.
یعنی اگر سری همگرا باشد، باقیمانده سری به سمت صفر میل خواهدکرد.
3-5 سریهای توابع
در این قسمت ازآموزش لینوم به سراغ سریهای توابع میرویم.
ما غالبا علاقمندیم رفتار سریهایی از توابع روی حوزه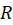 به شکل
به شکل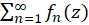 را مطالعه کنیم.
را مطالعه کنیم.
یک چنین سریهایی روی 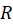 همگرا نامیده میشوند اگر سری برای هر مقدار
همگرا نامیده میشوند اگر سری برای هر مقدار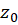 در
در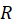 به
به 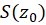 همگرا گردد. در این صورت مینویسیم:
همگرا گردد. در این صورت مینویسیم: 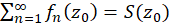 . را مقدار سری در
. را مقدار سری در 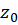 می نامند.
می نامند.
با توجه بهقضیه2نتیجه میگیریم که شرط لازم و کافی برای همگرایی سری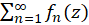 در حوزه
در حوزه 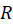 ، همگرایی سریهای حقیقی
، همگرایی سریهای حقیقی 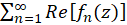 و
و 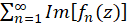 در
در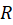 است.
است.
همچنین از آزمونهای تشخیص رفتار سریهای حقیقی میتوان به سادگی برای سریهای مختلط استفاده کرد. در زیر به آزمون نسبت اشاره میکنیم:
آزمون نسبت:سری 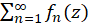 همگراست اگر حد
همگراست اگر حد 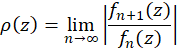 کوچکتر از یک گردد. اگر این حد بزرگ تر از یک شد، سری واگراست. در حالتی که مقدار حد برابر یک شود، هیچ نتیجهای در مورد رفتار سری حاصل نمیشود و باید از سایر آزمونهای تشخیص رفتار استفاده کرد.
کوچکتر از یک گردد. اگر این حد بزرگ تر از یک شد، سری واگراست. در حالتی که مقدار حد برابر یک شود، هیچ نتیجهای در مورد رفتار سری حاصل نمیشود و باید از سایر آزمونهای تشخیص رفتار استفاده کرد.
دقت کنید که در مورد همگرایی معمولی، برای تعیین مقدار سری با دقتی دلخواه نمیتوان حدی برای تعداد جملات سری قرارداد.
معمولا برای تحقیق همگرایی یکنواخت یک سری از آزمون زیر موسوم بهآزمون وایراشتاساستفاده میشود.
آزمون وایراشتاس:اگر دنباله عددی مثبتی چون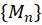 موجود باشد به طوری که برای همه مقادیر
موجود باشد به طوری که برای همه مقادیر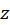 در ناحیه
در ناحیه 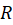 و تمام
و تمام 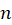 های صحیح، داشتهباشیم
های صحیح، داشتهباشیم 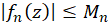 ، در اینصورت اگر سری
، در اینصورت اگر سری 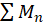 همگرا باشد، آنگاه سری
همگرا باشد، آنگاه سری 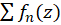 در ناحیه
در ناحیه 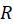 همگرای یکنواخت است.
همگرای یکنواخت است.
برای اثبات کافیست از رابطه زیر و همچنین همگرایی سری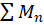 استفاده کنیم:
استفاده کنیم:
میتوان نشان داد:
1- حاصل جمع یک سری همگرای یکنواخت از توابع پیوسته، پیوسته است.
یعنی اگر 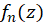 برای هر
برای هر 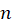 در ناحیه
در ناحیه 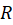 پیوسته بوده و
پیوسته بوده و 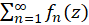 در
در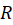 همگرای یکنواخت باشد، آنگاه
همگرای یکنواخت باشد، آنگاه 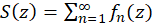 در ناحیه
در ناحیه 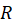 پیوسته است.
پیوسته است.
2- حاصل جمع یک سری همگرای یکنواخت از توابع تحلیلی، تحلیلی است و از آن میتوان جمله به جمله مشتق یا انتگرال گرفت.
4-5 سری های توانی و روش حل سری های توانی
حال ما به یکی از اساسیترین ابزار در آنالیز توابع مختلط، یعنیسریهای توانی میپردازیم.
یک سری به شکل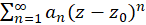 ، که در آن
، که در آن 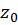 یک عدد مختلط،
یک عدد مختلط، 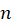 یک عدد طبیعی، و دنباله
یک عدد طبیعی، و دنباله 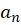 یک دنباله مختلط است، یکسری توانینامیده میشود.
یک دنباله مختلط است، یکسری توانینامیده میشود.
به سادگی میتوان با استفاده ازآزمون نسبتناحیه همگرایی یک سری توانی را مشخص نمود.
اگر 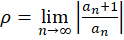 موجود یا برابر بینهایت شود، آنگاه
موجود یا برابر بینهایت شود، آنگاه
1) اگر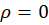 ، سری برای همه
، سری برای همه 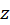 ها همگرای مطلق است.
ها همگرای مطلق است.
سری برای همه 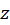 ها همگرای مطلق است.
ها همگرای مطلق است.
2) اگر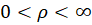 ، سری برای همه
، سری برای همه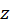 هایی که
هایی که 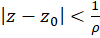 همگرا و برای
همگرا و برای 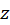 هایی که
هایی که 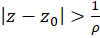 واگرا است.
واگرا است.
3) اگر 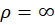 ، سری فقط در نقطه
، سری فقط در نقطه 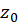 همگرا است.
همگرا است.
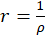 راشعاع همگرایی،دایره
راشعاع همگرایی،دایره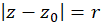 رادایره همگرایی،قرص
رادایره همگرایی،قرص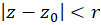 راقرص همگراییسری مینامیم.
راقرص همگراییسری مینامیم.
 مثال5 )شعاع همگرایی سری توانی
مثال5 )شعاع همگرایی سری توانی 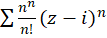 را تعیین کنید.
را تعیین کنید.
حل:شعاع همگرایی برابر است با:
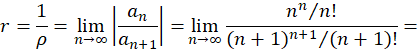
پس دایره همگرایی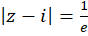 و قرص همگرایی
و قرص همگرایی 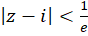 است.
است.
▄
با استفاده از آزمون وایراشتاس، میتوان نشانداد که هر سری توانی در داخل قرص همگرایی خود همگرای یکنواخت است، بنابراین چون تمامی جملات یک سری توانی، تحلیلی هستند؛ نتیجه میگیریم که هر سری توانی در قرص همگرایی خود تحلیلی بوده و از آن میتوان جمله به جمله مشتق یا انتگرال گرفت.
5-5 بسط تیلور توابع و روش حل بسط تیلور توابع

قضیه 3:فرضکنید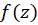 در حوزه
در حوزه 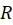 شامل نقطه
شامل نقطه 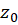 ، تحلیلی باشد. در این صورت میتوان
، تحلیلی باشد. در این صورت میتوان 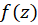 را در داخل قرص
را در داخل قرص 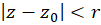 در ناحیه
در ناحیه 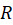 با بسط سری توانی زیر موسوم بهبسط تیلورتابع جانشین کرد.
با بسط سری توانی زیر موسوم بهبسط تیلورتابع جانشین کرد.
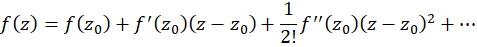
بنابراین بسط تیلور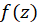 ، یک جانشین معتبر برای تابع، در کلیه نقاط داخل دایرهای به مرکز
، یک جانشین معتبر برای تابع، در کلیه نقاط داخل دایرهای به مرکز 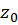 است که در آن
است که در آن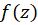 تحلیلی است. علاوه بر آن با توجه به روش تعیین ضرایب بسط، نتیجه میگیریم که یک چنین بسطی برای تابع منحصربه فرد است، یعنی اگر بتوان به هر روشی یک چنین بسطی را برای تابع بهدست آورد، این بسط همان بسط تیلور
تحلیلی است. علاوه بر آن با توجه به روش تعیین ضرایب بسط، نتیجه میگیریم که یک چنین بسطی برای تابع منحصربه فرد است، یعنی اگر بتوان به هر روشی یک چنین بسطی را برای تابع بهدست آورد، این بسط همان بسط تیلور 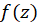 است و شعاع همگرایی سری برابر فاصله
است و شعاع همگرایی سری برابر فاصله 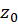 تا نزدیکترین نقطه غیرتحلیلی تابع
تا نزدیکترین نقطه غیرتحلیلی تابع 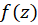 است. همچنین چون بسط تیلور یک سری توانی است، بنابراین از آن میتوان در ناحیه همگرایی جمله به جملهمشتق یاانتگرال گرفت.
است. همچنین چون بسط تیلور یک سری توانی است، بنابراین از آن میتوان در ناحیه همگرایی جمله به جملهمشتق یاانتگرال گرفت.
بسط تیلور توابع مقدماتی
به سادگی میتوان بسط تیلور توابع 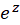 و
و 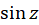 را به روش مستقیم محاسبه کرد:
را به روش مستقیم محاسبه کرد:
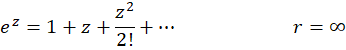
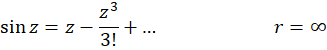
چون این توابع فاقد نقطه غیرتحلیلی هستند. پس شعاع همگرایی (یا اعتبار) هر دو بسط، بینهایت است. در جدول زیر بسطهای برخی از مهم ترین توابع، شعاع همگرایی و روش تعیین آنها به روش غیرمستقیم بیان شدهاست.
(مشتقگیری از 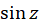 )
) 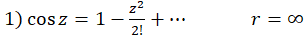
(با استفاده از 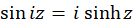 )
) 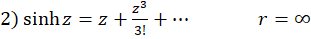
(بامشتقگیری از 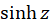 )
) 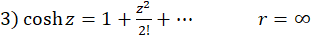
(با تقسیم صورت بر مخرج) π2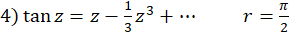
(با تقسیم صورت بر مخرج) 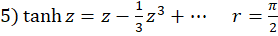
(با تقسیم صورت بر مخرج) 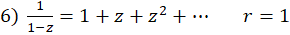
(استفاده از بسط خیام) ،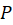 عدد صحیح منفی
عدد صحیح منفی 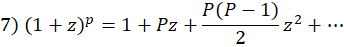
 مثال6 )بسط تیلور توابع زیر را حول نقاط مشخص شده بهدستآورده و قرص همگرایی هر یک را مشخص کنید.
مثال6 )بسط تیلور توابع زیر را حول نقاط مشخص شده بهدستآورده و قرص همگرایی هر یک را مشخص کنید.
الف- 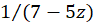 حول
حول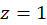 .
.
با فرض 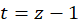 داریم:
داریم:
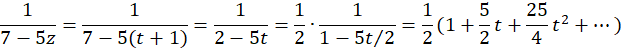
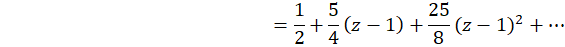
چون تنها نقطه منفرد تابع 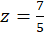 است، پس سری در قرص
است، پس سری در قرص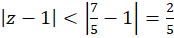 همگراست.
همگراست.
ب- 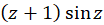 حول
حول 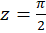 .
.
با فرض 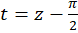 داریم:
داریم:
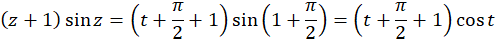
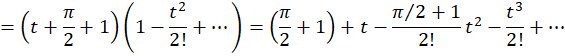
چون تابع در کلیه نقاط تحلیلی است پس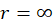 .
.
پ- 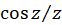 حول نقطه
حول نقطه 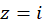 .
.
با فرض 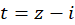 داریم:
داریم:
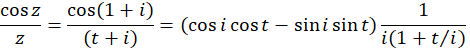
شعاع همگرایی سری فوق 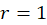 بوده و بسط در ناحیه
بوده و بسط در ناحیه 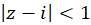 همگراست.
همگراست.
▄
6-5 بسطلوران توابع و روش حل بسط تیلور توابع
بسطهای تیلور توابع ما را قادر میسازند تا بسطهایسری توانی جانشین در همسایگی نقاطی که توابع در آن نقاط تحلیلی هستند، به دست میآوریم. پس این بسط ها را نمیتوان برای توابعی چون  یا
یا 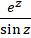 در نقطه
در نقطه 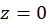 نتیجه گرفت، چون این توابع در
نتیجه گرفت، چون این توابع در 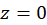 تحلیلی نیستند. برای یک چنین توابعی بسط دیگری موسوم بهبسط لورانموجوداست که از توانهای منفی برای استفاده میکند. این بسطها که با توجه به ملاحظات زیر نتیجه میشوند، به خصوص در مطالعه نقاط تکین توابع، که به یکی از نتایج اساسی توابع تحلیلی یعنی قضیهحسابماندههامنجر میگردد، مهم میباشند.
تحلیلی نیستند. برای یک چنین توابعی بسط دیگری موسوم بهبسط لورانموجوداست که از توانهای منفی برای استفاده میکند. این بسطها که با توجه به ملاحظات زیر نتیجه میشوند، به خصوص در مطالعه نقاط تکین توابع، که به یکی از نتایج اساسی توابع تحلیلی یعنی قضیهحسابماندههامنجر میگردد، مهم میباشند.
یک سری به شکل 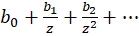 را میتوان به عنوان یک سری توای برحسب متغیر
را میتوان به عنوان یک سری توای برحسب متغیر  در نظرگرفت. اگر
در نظرگرفت. اگر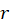 شعاع همگرایی این سری باشد، آنگاه سری برای
شعاع همگرایی این سری باشد، آنگاه سری برای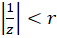 یا
یا 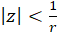 همگرای مطلق و برای
همگرای مطلق و برای 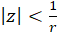 واگراست. ترکیب یک سری به شکل فوق و یک سری توانی معمولی، یک سری به صورت
واگراست. ترکیب یک سری به شکل فوق و یک سری توانی معمولی، یک سری به صورت 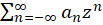 را نتیجه میدهد که شامل دو بخش است.
را نتیجه میدهد که شامل دو بخش است.
بخش اول سری: 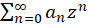 یک سری توانی است و فرض کنید در قرص
یک سری توانی است و فرض کنید در قرص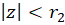 همگراست.
همگراست.
بخش دوم سری: 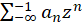 است که یک سری توانی برحسب
است که یک سری توانی برحسب  است و فرض کنید در ناحیه
است و فرض کنید در ناحیه  همگراست. در این صورت برای
همگراست. در این صورت برای 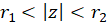 ، سری
، سری 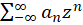 موسوم به سری لوران همگرا گردیده و در این ناحیه تحلیلی است.
موسوم به سری لوران همگرا گردیده و در این ناحیه تحلیلی است.
مشابه آن، سری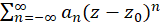 در ناحیه
در ناحیه 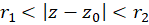 یک تابع تحلیلی است. ما یک چنین بسطی راسری لورانحول نقطه مینامیم. میتوان نشان داد که یک تابع تحلیلی در
یک تابع تحلیلی است. ما یک چنین بسطی راسری لورانحول نقطه مینامیم. میتوان نشان داد که یک تابع تحلیلی در 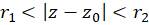 دارای بسط لوران در این ناحیه است.
دارای بسط لوران در این ناحیه است.
قضیه4 :اگر 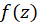 در ناحیه
در ناحیه 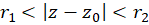 تحلیلی باشد، در این صورت میتوان آن را به شکلی منحصربه فرد، به صورت سری لوران:
تحلیلی باشد، در این صورت میتوان آن را به شکلی منحصربه فرد، به صورت سری لوران:
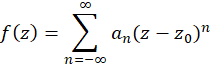
نمایش داد که در آن ضرایب بسط برای 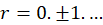 عبارت اند از:
عبارت اند از:
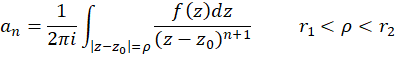
معمولا در عمل، ضرایب بسط را مستقیما از روی انتگرال ها محاسبه نمیکنند بلکه با توجه به منحصربه فرد بودن بسط از روش های غیرمستقیم به تعیین ضرایب میپردازند.
از بسطهای لوران به خصوص برای تعیین بسط توابع تحلیلیحول نقاط تکین تنهایی آنهااستفاده میشود. اگر 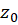 یک نقطه تکین تنها تابع تحلیل
یک نقطه تکین تنها تابع تحلیل 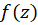 باشد، بسط لوران
باشد، بسط لوران 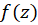 موجود و در حوزه
موجود و در حوزه 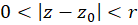 معتبر است که در آن
معتبر است که در آن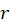 برابر فاصله نقطه
برابر فاصله نقطه 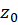 تا نزدیکترین نقطه تکین تابع
تا نزدیکترین نقطه تکین تابع 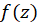 است.
است.
 مثال7 )بسطهای لوران توابع زیر را در همسایگی نقطه
مثال7 )بسطهای لوران توابع زیر را در همسایگی نقطه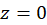 تعیین کرده و دامنه همگرایی آنها را بهدستآورید.
تعیین کرده و دامنه همگرایی آنها را بهدستآورید.
الف-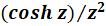
چون بسط 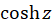 حول
حول 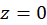 برابر
برابر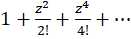 است، پس داریم:
است، پس داریم:
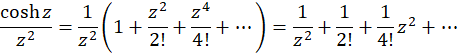
تابع فوق در حلقه 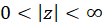 همگراست، زیرا فاقد نقطه تکین دیگری به جز
همگراست، زیرا فاقد نقطه تکین دیگری به جز 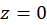 است.
است.
ب-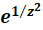
چون بسط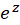 حول
حول 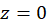 برابر
برابر 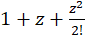 است، پس داریم:
است، پس داریم:
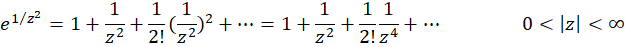
▄
7-5 محاسبه انتگرال با استفاده از بسط لوران توابع

این واقعیت که ما این بسطها را بدون استفاده از نظریه عمومی آنها محاسبه کردیم، بدین معنی است که میتوانانتگرالهای متناظر با ضرایب بسط را با مقایسه آنها با مقادیر عددی ضرایبی که یافتهایم بهدستآورد. به عنوان مثال، چون بسط لوران تابع 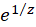 حول
حول 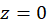 برابر است با:
برابر است با:
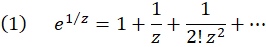
و ضرایب بسط لوران از فرمول 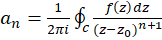 محاسبه میشود که در آن
محاسبه میشود که در آن 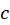 هر خم ساده بستهای در ناحیه اعتبار بسط است، پس نتیجه میگیریم که برای
هر خم ساده بستهای در ناحیه اعتبار بسط است، پس نتیجه میگیریم که برای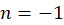 :
:
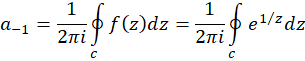
ولی با توجه به بسط (1) ، 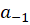 ضریب جمله
ضریب جمله  بوده و برابر عدد
بوده و برابر عدد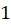 است، پس :
است، پس :
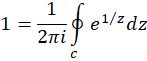
یا