6)نظریه حساب ماندهها و روش حل ماندهها

در اینآموزش کپسولی لینوم به یکی از مهمترینروش های انتگرالگیری در توابع مختلط، یعنی انتگرال گیری با استفاده از بسطهای لوران توابع و قضیه حساب ماندهها خواهیم پرداخت. سپس کاربرد این نظریه را در حل پارهای از انتگرالهای حقیقی بررسی میکنیم.
ابتدا مفاهیم صفر تابع و نقاط تکین یک تابع را مرور و گسترش میدهیم.
1-6 صفرهای توابع و مرتبه آنها
نقطه را که در آن
را که در آن  ، یکصفرتابع
، یکصفرتابع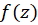 میخوانیم. صفر یک تابع تحلیلی را ازمرتبه
میخوانیم. صفر یک تابع تحلیلی را ازمرتبه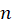 نامیم اگر
نامیم اگر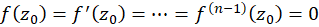 ، ولی مشتق
، ولی مشتق 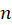 اُم آن
اُم آن 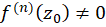 باشد.
باشد.
 مثال 1)صفرهای تابع
مثال 1)صفرهای تابع 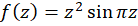 را تعیین کرده و مرتبه آنها را بیابید.
را تعیین کرده و مرتبه آنها را بیابید.
حل: وقتی 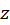 یک عدد صحیح باشد،
یک عدد صحیح باشد، 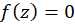 است. در
است. در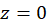 داریم:
داریم:
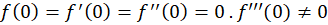
پس 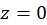 یک صفر مرتبه سوم تابع است.
یک صفر مرتبه سوم تابع است.
این نتیجه را همچنین میتوانستیم از بسط مک-لورن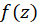 نیز به دستآوریم.
نیز به دستآوریم.
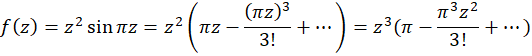
درسایر صفرهای 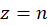 برای
برای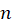 صحیح غیرصفر، داریم
صحیح غیرصفر، داریم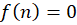 ولی
ولی 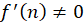 ، پس سایر صفرهای تابع از مرتبه یک هستند.
، پس سایر صفرهای تابع از مرتبه یک هستند.
میتوان نشانداد که اگر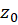 ، صفر یک تابع تحلیلی باشد، آنگاه همسایگی از
، صفر یک تابع تحلیلی باشد، آنگاه همسایگی از 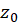 موجوداست که در آن همسایگی تابع دارای صفر دیگری نیست. به عبارت دیگر:
موجوداست که در آن همسایگی تابع دارای صفر دیگری نیست. به عبارت دیگر:
صفرهای یک تابع تحلیلی، تکین هستند.
به سادگی میتوان بررسی کرد که کلیه صفرهای توابع 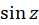 ،
، 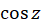 ،
،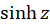 ،
،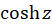 و
و 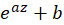 از مرتبه یک هستند. همچنین
از مرتبه یک هستند. همچنین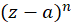 برای
برای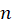 طبیعی، دارای صفری در نقطه
طبیعی، دارای صفری در نقطه 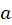 از مرتبه
از مرتبه 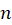 است. اگر
است. اگر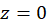 صفر مشترک توابع
صفر مشترک توابع 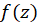 و
و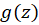 به ترتیب از مرتبههای
به ترتیب از مرتبههای 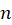 و
و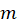 برای
برای باشد، آنگاه
باشد، آنگاه 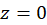 صفر تابع:
صفر تابع:
1- 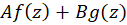 از مرتبه
از مرتبه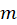 است. (
است. (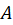 و
و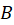 مخالف صفر)
مخالف صفر)
2- 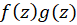 از مرتبه
از مرتبه 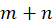 است.
است.
با استفاده از این خواص می توان با روش سریعتری مرتبه صفرهای توابع را تعیین کرد.
2-6 نقاط تکین توابع و انواع آنها
نقطه را یک نقطه تکین تابع
را یک نقطه تکین تابع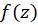 نامیم اگر
نامیم اگر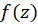 در
در 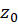 تحلیلی نبوده ولی هر همسایگی از آن شامل نقطهای باشد که تابع در آن نقطه تحلیلی است. نقطه تکین
تحلیلی نبوده ولی هر همسایگی از آن شامل نقطهای باشد که تابع در آن نقطه تحلیلی است. نقطه تکین 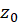 راتنهانامیم اگر همسایگی از
راتنهانامیم اگر همسایگی از 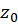 موجود باشد که
موجود باشد که 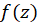 در آن همسایگی شامل نقطه تکین دیگری نگردد. میدانیم که اگر
در آن همسایگی شامل نقطه تکین دیگری نگردد. میدانیم که اگر 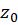 یک نقطه تکین تنهای تابع باشد، آنگاه
یک نقطه تکین تنهای تابع باشد، آنگاه 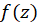 دارای بسط لوران حول
دارای بسط لوران حول 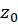 بوده و این بسط جانشین
بوده و این بسط جانشین 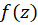 در ناحیه بین دو دایره است که شعاع خارجی آن برابر فاصله
در ناحیه بین دو دایره است که شعاع خارجی آن برابر فاصله 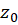 از نزدیکترین نقطه تکین
از نزدیکترین نقطه تکین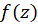 و شعاع داخلی آن به اندازه دلخواه کوچک است.
و شعاع داخلی آن به اندازه دلخواه کوچک است.
اگر بسط لوران 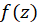 در همسایگی از نقطه تکین تنهای
در همسایگی از نقطه تکین تنهای 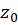 فقط شامل تعدادی متناهی توانهای منفی از
فقط شامل تعدادی متناهی توانهای منفی از 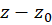 باشد، آنگاه نقطه
باشد، آنگاه نقطه 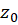 را یکقطب
را یکقطب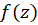 مینامیم. اگر
مینامیم. اگر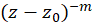 بزرگترین جمله شامل توان منفی موجود در بسط باشد، قطب را ازمرتبه
بزرگترین جمله شامل توان منفی موجود در بسط باشد، قطب را ازمرتبه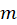 خوانده و حاصل جمع تمام جملات شامل توانهای منفی یعنی
خوانده و حاصل جمع تمام جملات شامل توانهای منفی یعنی 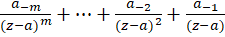 رابخش اصلی
رابخش اصلی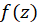 در
در 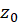 مینامیم.
مینامیم.
اگر بسط لوران 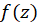 در هر همسایگی از نقطه تکین تنهای
در هر همسایگی از نقطه تکین تنهای 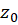 شامل تعداد بی شماری جمله از توانهای منفی
شامل تعداد بی شماری جمله از توانهای منفی باشد، آنگاه
باشد، آنگاه 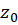 را یکنقطه تکین اساسی
را یکنقطه تکین اساسی 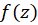 یا قطب از مرتبه بینهایت مینامیم. همچنین اگر بسط لوران
یا قطب از مرتبه بینهایت مینامیم. همچنین اگر بسط لوران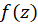 در نقطه تکین تنهای
در نقطه تکین تنهای 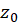 فاقد جملهای با توان منفی از
فاقد جملهای با توان منفی از باشد، آنگاه
باشد، آنگاه 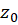 را یکنقطه تکین برطرفشدنی یا قطب از مرتبه صفرتابع میخوانیم.
را یکنقطه تکین برطرفشدنی یا قطب از مرتبه صفرتابع میخوانیم.

دو روش دیگر تعیین نوع نقطه تکین و مرتبه قطب در نقطه تکین تنهای 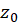 برای تابع
برای تابع به جز استفاده از بسط لوران تابع در نقطه
به جز استفاده از بسط لوران تابع در نقطه 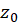 ، به قرار زیر است:
، به قرار زیر است:
روش اول: 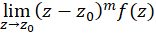 را برای
را برای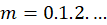 به ترتیب محاسبه میکنیم تا زمانی که برای اولین بار مقداری متناهی برای حد نتیجه شود. اولین مقداری از
به ترتیب محاسبه میکنیم تا زمانی که برای اولین بار مقداری متناهی برای حد نتیجه شود. اولین مقداری از 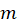 که به ازای آن حد فوق متناهی میشود، مرتبه قطب است. اگر
که به ازای آن حد فوق متناهی میشود، مرتبه قطب است. اگر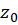 یک نقطه تکین اساسی باشد، در این صورت حد برای هیچ مقدار
یک نقطه تکین اساسی باشد، در این صورت حد برای هیچ مقدار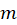 متناهی نمیگردد.
متناهی نمیگردد.
روش دوم: مراجعه به مرتبه صفر صورت و مخرج در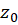 . مرتبه قطب برابر تفاضل مرتبه صفر صورت از مرتبه صفر مخرج است. قطب مرتبه اول راقطب ساده نیز مینامند. نقاط تکین برطرف شدنی یا اساسی را به ترتیب قطبهای تابع از مرتبههای صفر و بینهایت نیز میخوانند.
. مرتبه قطب برابر تفاضل مرتبه صفر صورت از مرتبه صفر مخرج است. قطب مرتبه اول راقطب ساده نیز مینامند. نقاط تکین برطرف شدنی یا اساسی را به ترتیب قطبهای تابع از مرتبههای صفر و بینهایت نیز میخوانند.
توجه کنید که چون صفرهای توابع تحلیلی تنها هستند لذا وقتی این صفرها در مخرج کسرها واقع شوند، نقاط تکین تنها را نتیجه میدهند. به عنوان مثال تابع 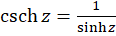 دارای بینهایت نقطه تکین تنها در
دارای بینهایت نقطه تکین تنها در برای
برای 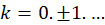 است که چون صفرهای مرتبه اول تابع
است که چون صفرهای مرتبه اول تابع 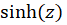 می باشند، پس قطبهای مرتبه اول
می باشند، پس قطبهای مرتبه اول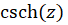 هستند.
هستند.
 مثال2 )نقاط تکین توابع زیر را تعیین کنید.
مثال2 )نقاط تکین توابع زیر را تعیین کنید.
الف-
حل:تابع دارای نقاط تکین در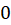 و
و 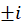 است.
است. 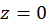 صفر مخرج از مرتبه دو و صفر صورت از مرتبه یک است، پس
صفر مخرج از مرتبه دو و صفر صورت از مرتبه یک است، پس 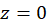 یک قطب ساده است. همچنین
یک قطب ساده است. همچنین 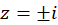 نیز قطبهای ساده
نیز قطبهای ساده 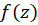 میباشند.
میباشند.
ب-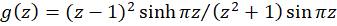
حل:نقاط تکین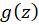 ،
، 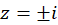 و
و 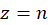 برای کلیه
برای کلیه 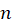 ها صحیح است.
ها صحیح است. 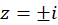 صفرهای مخرج از مرتبه یک و همچنین صفرهای
صفرهای مخرج از مرتبه یک و همچنین صفرهای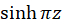 از مرتبه یک هستند، پس هردو نقاط قطب های برطرفشدنی اند.
از مرتبه یک هستند، پس هردو نقاط قطب های برطرفشدنی اند. 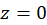 نیز صفر مشترک
نیز صفر مشترک 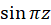 و
و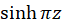 است. پس این نقطه نیز قطب برطرفشدنی است.
است. پس این نقطه نیز قطب برطرفشدنی است. 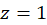 صفر مشترک صورت و مخرج بوده و یک قطب برطرفشدنی است. سایر نقاط تکین تابع یعنی
صفر مشترک صورت و مخرج بوده و یک قطب برطرفشدنی است. سایر نقاط تکین تابع یعنی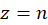 برای
برای 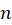 های صحیح غیرصفر و یک، قطبهای ساده این تابع میباشند.
های صحیح غیرصفر و یک، قطبهای ساده این تابع میباشند.
3-6 قضیه حساب ماندهها
در فصل قبل دیدیم که ضریب 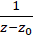 ، یعنی
، یعنی 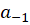 ، در بسط لوران تابع
، در بسط لوران تابع 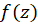 در همسایگی از نقطه تکین تنهای
در همسایگی از نقطه تکین تنهای 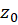 دارای اهمیت شایانی است، زیر که مقدار انتگرال
دارای اهمیت شایانی است، زیر که مقدار انتگرال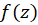 به آن بستگی دارد؛ یعنی برای هر خم ساده بسته
به آن بستگی دارد؛ یعنی برای هر خم ساده بسته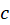 در ناحیه همگرایی بسط داریم:
در ناحیه همگرایی بسط داریم:
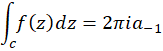
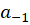 ، ضریب جمله
، ضریب جمله 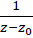 رامانده
رامانده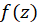 در نقطه
در نقطه 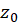 نامیده و آن را با
نامیده و آن را با 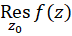 ،
، 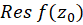 و یا
و یا 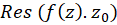 نمایشمیدهند. مفهوم فوق را میتوان به سادگی برای انتگرالگیری حول خمهایی که شامل چند نقطه تکین تنها هستند، گسترش داد.
نمایشمیدهند. مفهوم فوق را میتوان به سادگی برای انتگرالگیری حول خمهایی که شامل چند نقطه تکین تنها هستند، گسترش داد.
قضیه حساب ماندهها-اگر 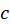 یک خم ساده بسته بوده و
یک خم ساده بسته بوده و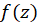 روی و داخل
روی و داخل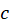 به جز تعداد متناهی نقاط تکین
به جز تعداد متناهی نقاط تکین 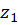 ،
، 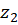 ، ... ،
، ... ،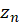 در داخل
در داخل 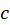 تحلیلی باشد، آنگاه:
تحلیلی باشد، آنگاه:
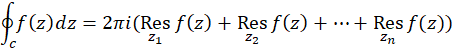
 مثال 3)مقدار مانده تابع زیر را حول نقطه
مثال 3)مقدار مانده تابع زیر را حول نقطه 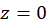 مشخص کنید.
مشخص کنید.
حل:
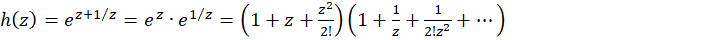
مقدار مانده برابر ضریب جمله  است، با جمع آوری این جملات داریم:
است، با جمع آوری این جملات داریم:
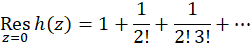
روش محاسبه ماندهها با استفاده از بسطهای لوران خستهکننده و طولانی است. روش سادهتر تعیین مانده در قطبهای متناهی با توجه به ملاحظات زیر نتیجه میشود:
فرض کنید 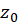 یک قطب مرتبه اول تابع
یک قطب مرتبه اول تابع 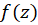 باشد، یعنی:
باشد، یعنی:
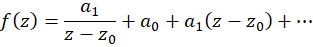
با ضرب طرفین در  و سپس میل دادن
و سپس میل دادن 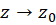 نتیجه میگیریم:
نتیجه میگیریم:
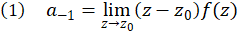
استفاده از فرمول فوق در تعیین مقدار مانده تابع 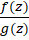 در قطب ساده
در قطب ساده 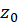 ، با فرض
، با فرض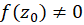 ، نتیجه ساده زیر را به دست میدهد.
، نتیجه ساده زیر را به دست میدهد.
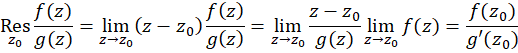
در محاسبه حد اول از قاعده هوپیتال استفاده شدهاست، پس داریم:
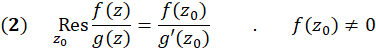
اگر 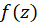 دارای قطب مرتبه دوم باشد، آنگاه :
دارای قطب مرتبه دوم باشد، آنگاه :
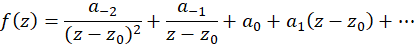
با ضرب طرفین در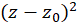 ومشتقگیری نسبت به
ومشتقگیری نسبت به 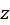 و سپس میلدادن
و سپس میلدادن 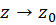 این بار داریم:
این بار داریم:
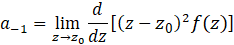
با استفاده از روشی مشابه، نتیجه میگیریم که اگر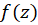 دارای قطب مرتبه
دارای قطب مرتبه 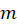 در نقطه
در نقطه 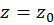 باشد، آنگاه مانده
باشد، آنگاه مانده 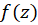 در
در 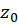 برابر است با:
برابر است با:
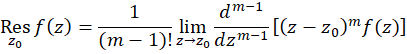
به دلیل طولانی بودن محاسبات، فرمول فوق برای تعیین مانده در قطبهای مرتبه دوم به بالا توصیهنمیشود مگر آنکه قطبها صفرهای یک چندجملهای در مخرج 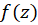 باشند. به هرحال به فرض استفاده از فرمول فوق بهتر است که مانند مثال زیر (قسمت الف) از بسطهای توابع استفادهگردد. در هر صورت برای تعیین مانده در قطبهای اساسی تنها روش، استفاده از بسط لوران توابع است. همچنین توجه کنید که مقدار مانده در قطبهای برطرفشدنی برابر صفر است.
باشند. به هرحال به فرض استفاده از فرمول فوق بهتر است که مانند مثال زیر (قسمت الف) از بسطهای توابع استفادهگردد. در هر صورت برای تعیین مانده در قطبهای اساسی تنها روش، استفاده از بسط لوران توابع است. همچنین توجه کنید که مقدار مانده در قطبهای برطرفشدنی برابر صفر است.
 مثال4 )مانده توابع زیر را در نقاط مشخصشده تعیین کنید.
مثال4 )مانده توابع زیر را در نقاط مشخصشده تعیین کنید.
الف-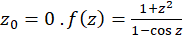
حل-چون 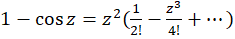 ، پس
، پس 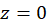 صفر مرتبه دوم تابع بوده و بنابراین قطب مرتبه دوم
صفر مرتبه دوم تابع بوده و بنابراین قطب مرتبه دوم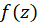 است و داریم:
است و داریم:
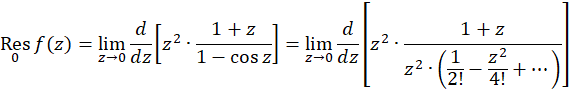
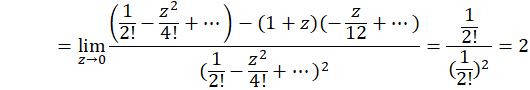
ب- 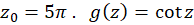
حل-چون 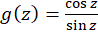 ، پس
، پس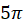 صفر مرتبه اول مخرج یا قطب ساده
صفر مرتبه اول مخرج یا قطب ساده 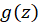 است و با استفاده از فرمول(1) داریم:
است و با استفاده از فرمول(1) داریم:
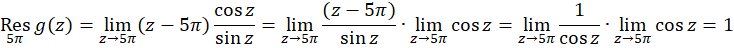
اگر در عوض از فرمول (2) استفاده میکردیم، آنگاه نتیجه سریعتر بهدستمیآمد:
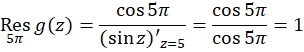
 مثال5 )انتگرال
مثال5 )انتگرال 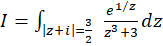 را حول مسیر مشخص شده مناسب محاسبه کنید.
را حول مسیر مشخص شده مناسب محاسبه کنید.
حل-تابع 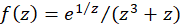 دارای دو نقطه تکین
دارای دو نقطه تکین 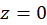 و
و 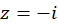 در داخل ناحیه است.
در داخل ناحیه است.
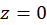 قطب اساسی و
قطب اساسی و 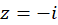 قطب ساده
قطب ساده 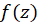 میباشند، پس چون بسط لوران تابع در
میباشند، پس چون بسط لوران تابع در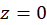 برابر است با:
برابر است با:
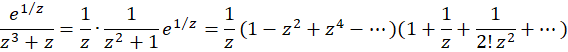
پس مقدار مانده در این نقطه برابر 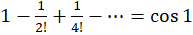 است.
است.
در قطب ساده 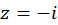 داریم:
داریم:
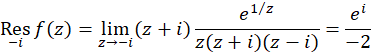
بنابراین مقدار انتگرال برابر است با:
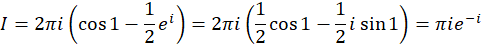

4-6 کاربرد انتگرالهای مختلط در محاسبه انتگرالهای حقیقی
در این بخش از آموزش ریاضی مهندسیلینوم، به کاربردهای انتگرال میپردازیم. برخی از انتگرالهای حقیقی را میتوان با انتخاب تابع مناسب  روی مسیر مناسب
روی مسیر مناسب 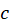 محاسبه نمود. در این بخش میخواهیم به بیان چند روش مفید برای محاسبه پارهای انتگرالهای معین حقیقی با استفاده از حساب ماندهها بپردازیم.
محاسبه نمود. در این بخش میخواهیم به بیان چند روش مفید برای محاسبه پارهای انتگرالهای معین حقیقی با استفاده از حساب ماندهها بپردازیم.
1) 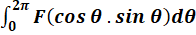
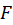 تابعی گویا از
تابعی گویا از و
و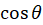 است که برای کلیه مقادیر
است که برای کلیه مقادیر 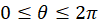 تعریف شدهاست. برای حل اینگونه انتگرالها
تعریف شدهاست. برای حل اینگونه انتگرالها 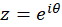 در نظرمیگیریم.
در نظرمیگیریم. 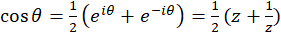 و
و 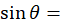 ، همچنین چون
، همچنین چون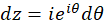 ، پس dθ=dziz
، پس dθ=dziz ، چون با تغییر
، چون با تغییر  ،
،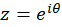 دایره واحد را میپیماید، پس داریم:
دایره واحد را میپیماید، پس داریم:
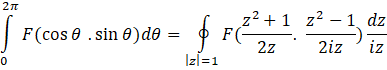
 مثال6 )
مثال6 ) 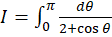 را محاسبه کنید.
را محاسبه کنید.
حل-چون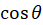 در فواصل
در فواصل 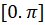 و
و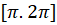 دارای مقادیر یکسانی است، پس با استفاده از تغییر متغییر
دارای مقادیر یکسانی است، پس با استفاده از تغییر متغییر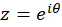 داریم:
داریم:
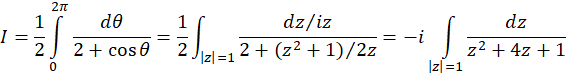
نقاط تکین تابع 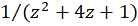 برابر
برابر 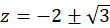 است و قطب ساده
است و قطب ساده 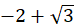 در داخل دایره قراردارد، پس:
در داخل دایره قراردارد، پس:
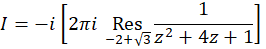
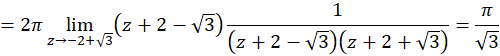
روش دیگر-اگر نقاط تکین تابع را 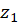 و
و 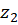 در نظربگیریم، آنگاه
در نظربگیریم، آنگاه 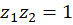 و
و 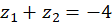 . فرض کنید
. فرض کنید 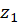 نقطه تکین داخل دایره واحد باشد، در اینصورت:
نقطه تکین داخل دایره واحد باشد، در اینصورت:
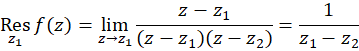
اما 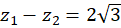 ، پس دوباره
، پس دوباره 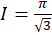 .
.
در سایر انتگرالهای این بخش باید تابع و مسیر به طریقی مناسب چنان انتخاب گردند که پس از محاسبه، انتگرال موردنظر پدید آید.
2) 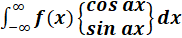
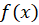 کسری گویاست که برای کلیه مقادیر حقیقی
کسری گویاست که برای کلیه مقادیر حقیقی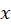 تعریف شدهاست و درجه چند جملهای مخرج آن حداقل دو واحد از درجه چندجملهای صورت بیشتر است ( این شرط برای همگرایی انتگرالها کافی است).در این صورت داریم:
تعریف شدهاست و درجه چند جملهای مخرج آن حداقل دو واحد از درجه چندجملهای صورت بیشتر است ( این شرط برای همگرایی انتگرالها کافی است).در این صورت داریم:
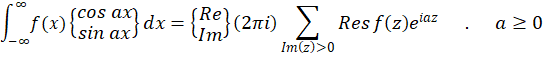
 مثال7)مقدار
مثال7)مقدار 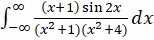 را حساب کنید.
را حساب کنید.
حل-ماندههای واقع در بالای محور حقیقی تابع 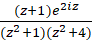 ، برابر
، برابر 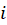 و
و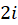 است که هر دو قطبهای ساده اند. چون:
است که هر دو قطبهای ساده اند. چون:
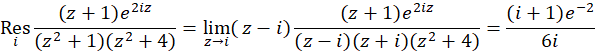
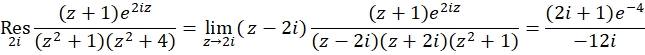
بنابراین مقدار انتگرال برابر است:
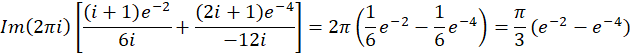
اگرانتگرالگیری را فراموش کردهبودید، میتوانیدکپسول آموزش انتگرالگیری را ببینید.