7) نگاشتهای مختلط و روش حل نگاشتهای مختلط مهم

تا این جا بااعداد مختلط آشنا شدیم. در اینآموزش کپسولی لینوم، به سراغ یادگیری نگاشت های مختلط میرویم.
برخلاف توابع حقیقی یک متغییره که دارای نمایش هندسی واقع در یک صفحه هستند، برای بررسی نمایش هندسیتوابع مختلط نیاز به دو صفحه داریم. صفحه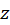 که مقادیر
که مقادیر 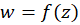 در دامنه تعریف تابع را در آن مشخص میکنیم و صفحه
در دامنه تعریف تابع را در آن مشخص میکنیم و صفحه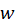 که مقادیر تابع
که مقادیر تابع 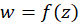 در آن تصویر میگردد. با این روش تابع
در آن تصویر میگردد. با این روش تابع 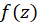 به نقطه
به نقطه 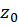 واقع در دامنه تعریف خود
واقع در دامنه تعریف خود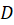 ، نقطه
، نقطه 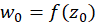 واقع در صفحه
واقع در صفحه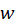 را تخصیص میدهند. در این صورت گوییم
را تخصیص میدهند. در این صورت گوییم 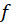 یکنگاشت از
یکنگاشت از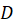 به صفحه
به صفحه 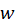 تعریفمیکند. برای هر نقطه
تعریفمیکند. برای هر نقطه 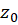 در
در  ،
، 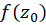 راتصویریانقشیاتبدیلیافته
راتصویریانقشیاتبدیلیافته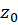 توسط نگاشت
توسط نگاشت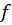 مینامند.
مینامند.
چون با مشخص کردن نقش چند نقطه نمیتوان اطلاعات چندانی درباره طرز عمل و خواص اصلی یک تابع بهدست آورد، به این منظور سعی میکنیم نقش نواحی یا خانوادهای از خمهای ساده (معمولا یک دسته خطوط موازی یا دوایر هم مرکز) را مطالعه کنیم. با این روش میتوانیم طبیعت مهندسیتوابع مختلط را با توجه به ویژگیهای آنها در انتقال خمها و نواحی معینی از صفحه مشاهده کنیم. در این فصل با خاصیت مهمی موسوم به خاصیتهمدیسی( ثابت نگاه داشتن اندازه و جهت زوایای بین خمها پس از انتقال) مطالعه میکنیم.
روش معمول برای مطالعه یک نگاشت، بررسی چگونگی انتقال یک دسته منحنی خاص توسط تابع است. برای تعیین نقش خم هموار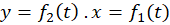 برای
برای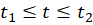 توسط نگاشت
توسط نگاشت 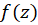 ، کافی است شکل پارامتری خم
، کافی است شکل پارامتری خم 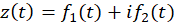 را در تابع جانشین کنیم تا منحنی تصویر آن به صورت
را در تابع جانشین کنیم تا منحنی تصویر آن به صورت 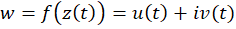 برای
برای 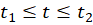 نتیجه شود.
نتیجه شود.
 مثال1 )نقش دایره
مثال1 )نقش دایره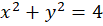 را توسط نگاشت
را توسط نگاشت 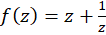 تعیین کنید.
تعیین کنید.
حل:شکل پارامتری دایره به صورت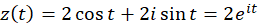 برای
برای 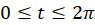 است، پس داریم:
است، پس داریم:
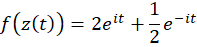
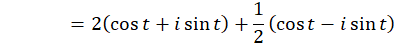
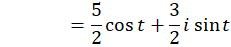
پس تصویر دایره، منحنی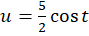 و
و 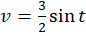 برای
برای 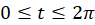 واقع در صفحه
واقع در صفحه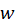 است، این منحنی نمایش بیضی افقی
است، این منحنی نمایش بیضی افقی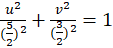 است.
است.
▄
به طور کلی هر تابع مختلط چون 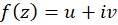 را میتوان به عنوانتبدیلی از فضای دوبعدی
را میتوان به عنوانتبدیلی از فضای دوبعدی 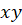 به فضای دوبعدی ملاحظه کرد که با زوج تبدیل زیر تعریف میشود :
به فضای دوبعدی ملاحظه کرد که با زوج تبدیل زیر تعریف میشود :

شرط لازم و کافی برای اینکه این تبدیل، یک ناحیه با مساحت غیرصفر را به ناحیه دیگری با مساحت غیرصفر تصویر کند آن است که 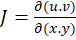 موسوم بهژاکوبیتبدیل مخالف صفر باشد.
موسوم بهژاکوبیتبدیل مخالف صفر باشد.
اگر  یک تابع تحلیلی در ناحیه
یک تابع تحلیلی در ناحیه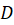 باشد، این شرط معادل با این است که :
باشد، این شرط معادل با این است که :
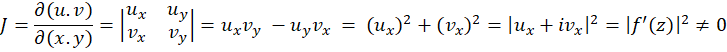
باشد، یعنی باید 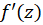 در کلیه نقاط ناحیه مخالف صفر باشد.
در کلیه نقاط ناحیه مخالف صفر باشد.
اگر مشتق تابع تحلیلی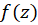 در حوزه
در حوزه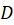 از صفحه
از صفحه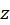 مخالف صفر باشد در اینصورت
مخالف صفر باشد در اینصورت 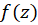 در حوزه
در حوزه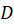 همدیساست. به عبارت دیگر اندازه و جهت زاویه بین هردو خم متقاطع در
همدیساست. به عبارت دیگر اندازه و جهت زاویه بین هردو خم متقاطع در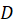 را پس از انتقال به صفحه
را پس از انتقال به صفحه 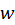 حفظ میکند. برای مشاهده این خاصیت فرض کنید
حفظ میکند. برای مشاهده این خاصیت فرض کنید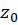 نقطهای در
نقطهای در 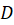 روی خم
روی خم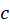 بوده و
بوده و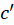 تصویر خم
تصویر خم 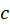 توسط نگاشت
توسط نگاشت 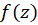 باشد. اگر
باشد. اگر 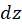 و
و 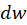 بهترتیب نمونههایکوچکی از دو منحنی
بهترتیب نمونههایکوچکی از دو منحنی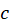 و
و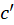 در
در 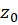 و
و 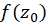 باشند، آنگاه چون
باشند، آنگاه چون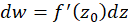 ، داریم:
، داریم:
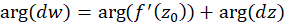
که در آن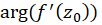 برای همه خمهای گذرنده از نقطه
برای همه خمهای گذرنده از نقطه 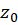 ثابت است.
ثابت است.
حال اگر خمهای 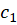 و
و 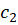 در نقطه
در نقطه 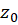 یکدیگر را تحت زاویه
یکدیگر را تحت زاویه  قطع کنند، یعنی
قطع کنند، یعنی 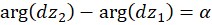 که در آن
که در آن 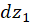 و
و  به ترتیبنمونههای متناظر با دو خم در نقطه
به ترتیبنمونههای متناظر با دو خم در نقطه 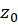 میباشند، آنگاه تصاویر آنها،
میباشند، آنگاه تصاویر آنها، 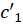 و
و 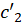 ، نیز تحت زاویه
، نیز تحت زاویه 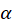 یکدیگر را در نقطه
یکدیگر را در نقطه 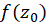 قطع خواهندکرد، زیرا اگر
قطع خواهندکرد، زیرا اگر 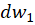 و
و 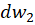 نمونههای متناظر با این دو خم در باشند، آنگاه:
نمونههای متناظر با این دو خم در باشند، آنگاه:
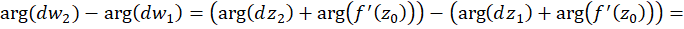
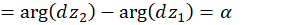
به عبارتی دیگر میتوان گفت:
قضیه-نگاشتی که توسط تابع تحلیلی 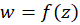 در حوزه
در حوزه 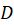 تعریف میشود، در هر نقطه
تعریف میشود، در هر نقطه 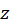 در
در  که برای آنها
که برای آنها 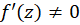 ، یک نگاشت همدیس است.
، یک نگاشت همدیس است.
نگاشتهای همدیس در ریاضیاتمهندسی نقش مهمی برعهده دارند. با استفاده از آنها میتوان روشی موثر برای حل مسائل مقدار مرزی دوبعدی در نظریه پتانسیل، با تبدیل نواحی پیچیده به نواحی سادهتر، بناکرد. در زیر به بررسی مهمترین نگاشتهای مختلط میپردازیم.
1-7 تعریف نگاشت نمایی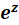 و روش حل آن
و روش حل آن
ما به طور معمول توابع مختلط را به گونهای تعریف میکنیم که 1) تحلیلی بوده و 2) با جایگذاری به همان تعریف آنالیز حقیقی برسیم. در اینجا، علاوه بر دو شرط بالا، دو شرط زیر را نیز انتخاب میکنیم:

حال با این فرضیات رابطه اویلر را ثابت کرده وتابع مختلط را بهدستمیآوریم:
را بهدستمیآوریم:
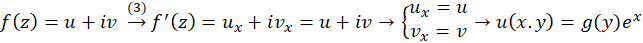
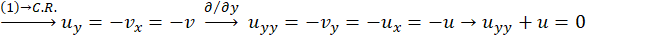

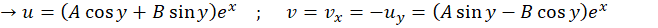
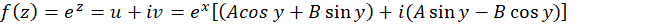
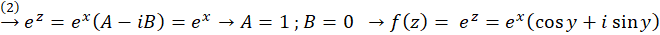

حال که تابع نمایی مختلط تعریف شد، میخواهیم ببینیم نگاشت آن به چه صورتی عمل میکند:
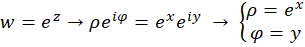
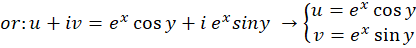
حال میتوان کنترل کرد که تابع تحلیلی بوده و مشتق آن با خودش برابر است.
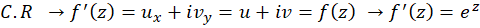
تابع فوق همواره همدیس است. زیرا همه جا تحلیلی بوده ونیز در هیچ نقطهای مشتق آن صفر نیست. زیرا :
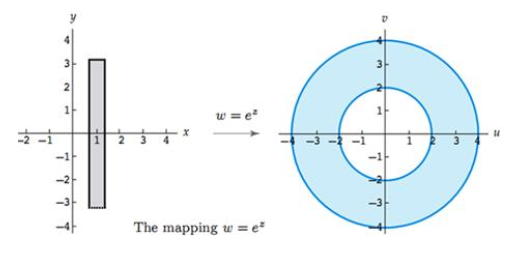
 مثال2 ) تبدیل یافته ناحیه
مثال2 ) تبدیل یافته ناحیه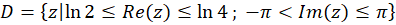 را تحت نگاشت
را تحت نگاشت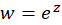 بیابید.
بیابید.
حل:
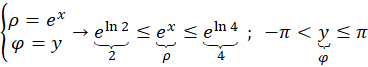
2-7 تعریف نگاشت توانی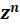 و روش حل آن
و روش حل آن
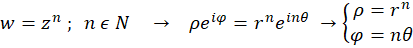
دقت شود که بایستی 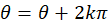 نوشته شود. اما از آنجا که با این انتخاب
نوشته شود. اما از آنجا که با این انتخاب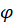 تغییری نمیکند و صرفا به همان نقطه میرود (زیرا
تغییری نمیکند و صرفا به همان نقطه میرود (زیرا 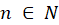 میباشد) ، لذا آن را به صورت
میباشد) ، لذا آن را به صورت  نوشتهایم. میتوان دو سمت رابطه را به فرمدکارتی(جمعی) نیز بیانکرد. در اینصورت:
نوشتهایم. میتوان دو سمت رابطه را به فرمدکارتی(جمعی) نیز بیانکرد. در اینصورت:
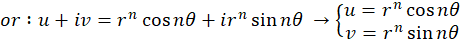
تابع همه جا تحلیلی است و چون صرفا در مبدامشتق صفر است لذا همه جا به جز مبدا همدیس است.
 مثال3 )تبدیل یافته یک نقطه تحت نگاشت
مثال3 )تبدیل یافته یک نقطه تحت نگاشت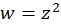 را ترسیم کرده، نشان دهید این نگاشت یکبهیک نیست.
را ترسیم کرده، نشان دهید این نگاشت یکبهیک نیست.
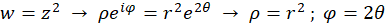
که در شکل زیر تبدیلیافته آن دیده میشود. همچنین به سادگی میتوان دید دونقطه قرینه نشان دادهشده در شکل زیر یعنی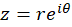 و
و 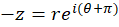 هردو به
هردو به 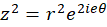 میروند، لذا یکبهیک نیست.
میروند، لذا یکبهیک نیست.
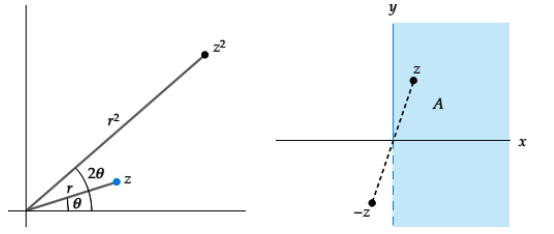
بنابراین هردونقطه 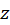 و
و 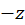 به یک نقطه نگاشت میشوند. برای یکبهیک شدن تابع، بایستی قسمتی از ناحیه را انتخاب کرد. در شکل سمت راست ناحیهای را که در آن تابع
به یک نقطه نگاشت میشوند. برای یکبهیک شدن تابع، بایستی قسمتی از ناحیه را انتخاب کرد. در شکل سمت راست ناحیهای را که در آن تابع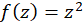 یکبهیک است نشانداده شدهاست. به طریق مشابه نگاشت
یکبهیک است نشانداده شدهاست. به طریق مشابه نگاشت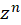 تبدیلی
تبدیلی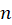 به یک خواهدبود.
به یک خواهدبود.

3-7 تعریف نگاشت شوارتز کریستوفل و روش حل آن
فرضکنید 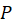 یک چندضلعی درصفحه
یک چندضلعی درصفحه 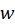 با رئوس
با رئوس 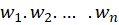 و زوایای داخلی متناظر
و زوایای داخلی متناظر 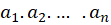 ، که در آن
، که در آن 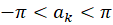 باشد. همچنین فرضکنید
باشد. همچنین فرضکنید 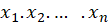 نقاطی متمایز بر محور حقیقی در صفحه
نقاطی متمایز بر محور حقیقی در صفحه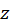 باشند. در اینصورت نگاشتی یکبهیک و همدیس موسوم به نگاشتشوارتز کریستوفلبه صورت
باشند. در اینصورت نگاشتی یکبهیک و همدیس موسوم به نگاشتشوارتز کریستوفلبه صورت 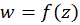 میتوان تعیین کرد به طوری که ناحیه
میتوان تعیین کرد به طوری که ناحیه 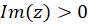 را به نحوی بر ناحیه
را به نحوی بر ناحیه 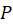 بنگارد که برای
بنگارد که برای 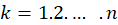 داشتهباشیم
داشتهباشیم 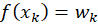 . این نگاشت به صورت:
. این نگاشت به صورت:
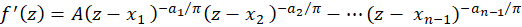
و یا
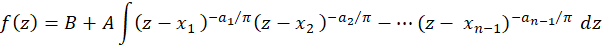
تعریف میشود که در آن 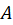 و
و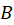 اعداد ثابت مناسبی میباشند با توجه به اندازه و موقعیت
اعداد ثابت مناسبی میباشند با توجه به اندازه و موقعیت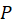 تعیین میگردند. دو نقطه از مجموعه نقاط
تعیین میگردند. دو نقطه از مجموعه نقاط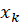 را میتوان به دلخواه انتخاب کرد.
را میتوان به دلخواه انتخاب کرد.
4-7 تعریف نگاشت یاکوفسکی و روش حل آن
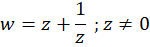
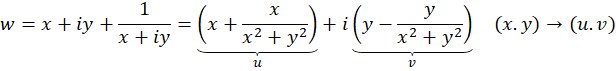
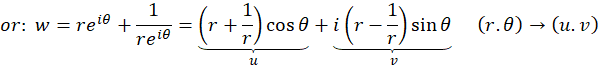
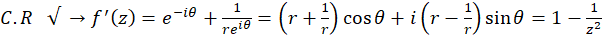
مشتق در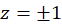 صفر است. لذا تابع فوق به جز در
صفر است. لذا تابع فوق به جز در 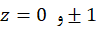 همواره همدیس است.
همواره همدیس است.
 مثال4 )تبدیلیافته دایره
مثال4 )تبدیلیافته دایره 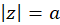 را تحت نگاشت یاکوفسکی بیابید.
را تحت نگاشت یاکوفسکی بیابید.
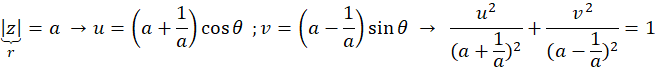
که یک بیضی است. در حالت خاص، دایره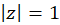 به پارهخط
به پارهخط 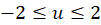 تبدیل میشود.
تبدیل میشود.
میتوان نشان داد تحت نگاشت کلیتر 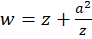 خواهیمداشت:
خواهیمداشت:
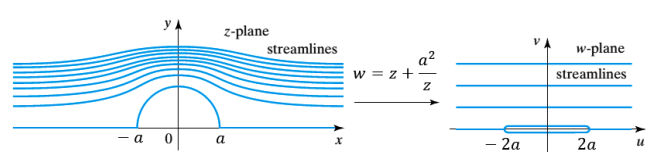
دیده میشود که نگاشت 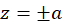 همدیس نیست و زوایا 2 برابر شدهاند؛ زیرا این نقاط ریشه ساده مشتق نگاشت میباشند
همدیس نیست و زوایا 2 برابر شدهاند؛ زیرا این نقاط ریشه ساده مشتق نگاشت میباشند 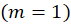 ، لذا زوایا در این نقاط
، لذا زوایا در این نقاط 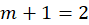 برابر میشوند.
برابر میشوند.
اگر مشتقگیری را فراموش کردهبودید، میتوانید کپسول آموزش مشتقگیری را ببینید.