تعادل و کشسانی

تعادل ایستا

یک جسم صُلب وقتی ساکن است، که در حال تعادل ایستا باشد. برای این جسم مجموع برداری نیروهای خارجی وارد شده صفر است.

(1-1)

اگر همه نیروهای در صفحه 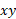 قرار داشته باشند این معادله برداری با دو معادله مولفه ای زیر هم ارز است

(1-2و3-1)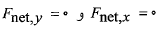

هم چنین تعادل ایستا ایجاب می کند که جمع برداریگشتاورهای نیروی خارجی وارد شده به جسم نسبت به هر نقطه ای صفر باشد یعنی

(1-4)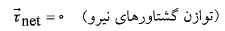

اگر نیروها در صفحه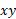 قرار داشته باشند تمام بردارهای گشتاور نیرو با محور 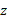موازی اند و معادله (4-1) با تنها معادله مولفه ای زیر هم ارز است

(1-5)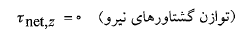

مسئله نمونه – توازن یک تیر افقی

در شکل زیر قسمت الف دو سر یک تیر تخته ای یکنواخت به طول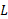 و جرم 1.8 کیلوگرم روی دو ترازو قرار دارند. جسم یکنواختی به جرم 2.7 کیلوگرم به حال سکون روی تیر قرار داردو فاصله مرکز ان تا انتهای سمت چپ تیر  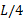است. ترازوها چه مقادیری را نشان می دهند؟

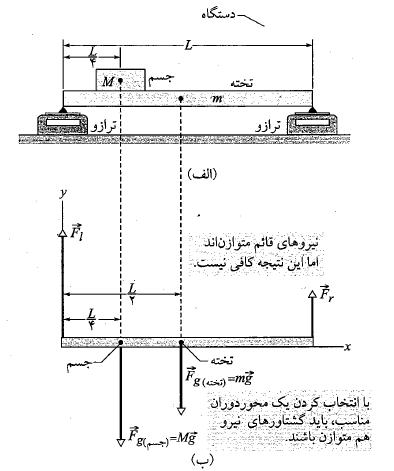
مرحله های نخستین حل کردن هر مسئله مربوط به تعادل ایستا را چنین پیگیری کنید: دستگاهی را که باید مورد تحلیل قرار گیرد به روشنی معرفی کنید. سپس نمودار جسم- آزاد دستگاه را رسم کنید و تمام نیروها را روی نمودار نشان دهید. اکنون تیر و جسم را با هم به عنوان دستگاه انتخاب کنید. آنگاه نیروهای وارد شده به دستگاه را روی نمودار جسم-آزاد قسمت ب شکل بالا نشان دهید. ( انتخاب دستگاه به تجربه نیاز دارد و اغلب ممکن است بیش از یک انتخاب خوب وجود داشته باشد).

چون دستگاه در حال تعادل ایستا است می توان از معادله های توازن نیروها  و معادله توازن گشتاورهای نیرو استفاده کرد.

محاسبات: نیروی عمودی وارد شده به تیر از سوی ترازوها 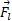 در سمت چپ و 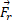در سمت راست هستند. مقادیر مورد نظر که با ترازوها نشان داده می شوند با بزرگی های این نیروها برابرند.نیروی گرانشی (تیر)  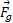به مرکز جرم تیر وارد می شود و برابر با 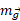است. به همین ترتیب نیروی گرانشی ( جسم) 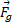که به مرکز جرم جسم وارد می شود برابر با  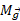 است.

اما برای ساده کردن قسمت ب شکل جسم را با یک خال واقع در میان دو سر تیر نشان می دهیم و بردار  را طوری رسم می کنیم که دمُ آن در همین محل باشد.( این جابه جایی 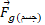   در راستای خط اثرش، گشتاور نیروی ناشی از 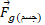را نسبت به هر محور عمود بر شکل تغییر نمی دهد).

در اینجا نیروها مولفه 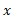ندارند، در نتیجه معادله  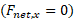هیچ اطلاعاتی به ما نمی دهد. برای مولفه های  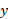از معادله  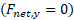استفاده می کنیم:

(2-13)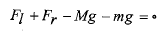

این معادله دو نیروی مجهول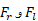 دارد. در نتیجه باید از معادله مربوط به توازن گشتاورهای نیرو استفاده کرد. این معادله را برای هر محور دوران عمود بر صفحه شکل می توان به کار برد. محوردوران را طوری انتخاب می کنیم که از انتهای چپ تیر بگذرد. در ضمن برای تعیین علامت گشتاورهای نیرو نیز از این قاعده کلی استفاده می کنیم: وقتی گشتاور نیرویی باعث چرخاندن جسم ساکنی به دور محور دوران می شود، علامتش در دوران ساعت گرد منفی و در دوران پادساعت گرد مثبت است.

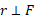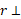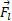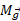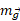سرانجام گشتاور نیرو را می توان از رابطه   r به دست آورد. بازوی گشتاور برای صفر، برای برابر با، برای  برابر با 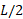و برای 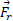برابر با 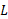است.

اکنون معادله توازن 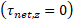 را می توان چنین نوشت

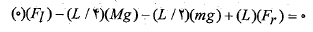
واز آنجا نتیجه می گیریم که

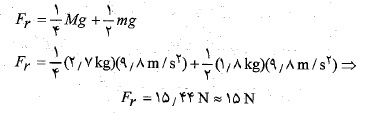
اکنون معادله (13-2) را نسبت به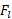 حل و نتیجه حل حاصل را در آن جانشانی می کنیم

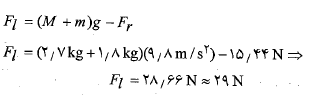
به جنبه های راهبردی حل مسئله توجه کنید: وقتی معادله ای را برای توازن مولفه های نیرو می نویسیم، با دو مجهول درگیر می شویم و وقتی معادله ای را برای گشتاورهای نیرو نسبت به یک محور اختیاری می نویسیم، باز هم با همان دو مجهول سر و کار خواهیم داشت. اما چون محور را طوری انتخاب کرده ایم که از نقطه اثر یکی از نیروهای مجهول در اینجا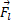 می گذرد، چنین گرفتاری ای پیش نیامده است. این گونه انتخاب محور، آن نیرو را از معادله گشتاور نیرو حذف می کند و اجازه می دهد که بزرگی نیروی مجهول دیگر 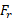را به دست آوریم. سپس با استفاده کردن از معادله توازن مولفه های نیرو، بزرگی نیروی مجهول باقی مانده را پیدا می کنیم.

مسئله نمونه- توازن برج لمیده پیزا

فرض می کنیم برج پیزا ( در ایتالیا) به صورت استوانه ای تو خالی یکنواخت به شعاع 9.8 متر و ارتفاع 60 متر است. محلمرکز جرم این استوانه در ارتفاع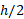  و در راستای محور مرکزی استوانه قرار دارد. استوانه در قسمت الف شکل زیر به صورت قائم و در قسمت ب شکل به اندازه زاویه به راست سو ( به سوی دیوار جنوبی برج) لمیده شده و در نتیجه مرکز جرم آن به اندازه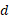 جا به جا شده است.

فرض می کنیم زمین به این برج تنها دو نیرو وارد می کند. نیروی عمودی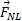 به دیوار سمت چپ ( دیوار شمالی)، ونیروی عمودی 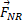به دیوار سمت راست ( دیوار جنوبی) وارد می شود. بزرگی بر اثر این لمیدگی چند درصد افزایش می یابد.

نکته: چون برج هنوز به حال ایستاده است، تعادل دارد و در نتیجه مجموع گشتاورهای نیروی حساب شده نسبت به هر نقطه باید صفر باشد. 

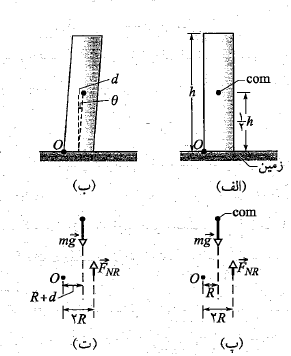
محاسبات: چون می خواهیم وارد شده به سمت راست را حساب کنیم و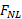 وارد شده به سمت چپ را نمی دانیم یا نمی خواهیم برای محاسبه گشتاورهای نیرو از یک نقطه چرخشگاه واقع در سمت چپ استفاده می کنیم. نیروهای وارد شده به برج قائم در قسمت پ شکل نشان داده شده اند.

نیروی گرانشی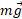 که فرض می کنیم به 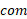وارد می شود دارای خط اثر قائم و بازوی گشتاور 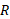( فاصله عمودی نقطه چرخشگاه تا خط اثر) است. گشتاور نیروی وابسته به این نیرو نسبت به نقطه چرخشگاه تمایل دارد یک دوران ساعت گرد ایجاد کند و در نتیجه منفی است.

نیروی عمودی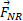 وارد شده به دیوار جنوبی نیز دارای خط اثر قائم و بازوی گشتاور 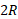است. گشتاور نیروی وابسته به این نیرو نسبت به نقطه چرخشگاه تمایل دارد یک دوران پادساعت گرد ایجاد کند و در نتیجه مثبت است. اکنون معادله توازن گشتاورهای نیرو 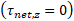را می توان به صورت زیر نوشت

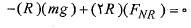
که از آنجا داریم

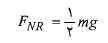
ما باید می توانستیم این نتیجه را حدس بزنیم چون مرکز جرم بر روی محور مرکزی ( خط تقارن استوانه) واقع شده است، سمت راست نصف وزن استوانه را نگه می دارد. در شکل قسمت ب مرکز جرم به اندازه

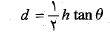
به راست سو جابه جا شده است. تنها تغییر به وجود آمده درتوازن معادله گشتاورهای نیرو این است که اکنون بازوی گشتاور مربوط به نیروی گرانشی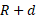 و بزرگی نیروی عمودی در سمت راست دارای بزرگی جدید 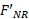است قسمت ت شکل.

بنابراین می توان نوشت

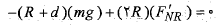
از آنجا که داریم

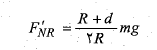
از تقسیم کردن این نتیجه جدید مربوط به نیروی عمودی طرف راست به نتیجه اولی می رسیم و سپس با جانشانی مقدار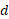 داریم

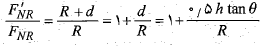
با جانشانی مقادیر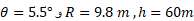 خواهیم داشت

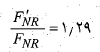
بنابراین مدل ساده ما پیشگویی می کند که لمیدگی اگرچه به نسبت کم است، نیروی عمودی وارد شده به دیوار جنوبی برج در حدود 30 درصد افزایش می یابد. یک خطر برای برج این است که این نیرو ممکن است به دیوار جنوبی فشار وارد کند و آن را به برون سو بترکاند. دلیل لمیدگی برج خاک تراکم پذیر زیر برج است، که با هر بارش باران وضعیت بدتر می شود. در سال های اخیر مهندسان برج را پایدارسازی کرده اند و با برقرار کردن یک سیستم زهکشی لمیدگی برج را تا حدی وارون کرده اند.

گرانیگاه

نیروی گرانشی به طور فردی به هر عنصر یک جسم وارد می شود. اثر خالص تمام اثرهای فردی را با این تصور می توان به دست آورد که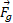،نیروی گرانشی کل هم ارز به نقطه خاصی به نام گرانیگاه وارد شود. اگر شتاب گرانشی 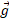برای تمام عنصرهای جسم یکسان باشد، گرانیگاه در مرکز جرم جسم واقع است.

مدول کشسانی

برای توصیف رفتار کشسانی ( تغییر شکل) اشیاء در پاسخ به نیروهای وارد شده از سه مدول کشسانی استفاده می شود. کرنش ( تغییر نسبی طول) از طریق یک مدول مناسب و طبق رابطه کلی زیر ، با تنش ( نیروی وارد شده به یکای سطح) رابطه خطی دارد:

(1-6)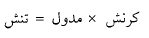

کشش و تراکم

وقتی شیئی تحت اثر کشش یا تراکم قرار می گیرد معادله فوق چنین نوشته می شود

(1-7)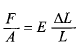

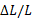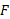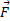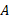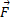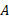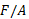که در آن کنش کششی یا تراکمی شیء، بزرگی نیروی وارد شده ، که کرنش را به وجود می آورد، مساحت مقطعی است که ( بطور عمود بر مطابق قسمت الف شکل به آن وراد می شود و مدول یانگ مربوط به شیء است. تنش برابر با   است.

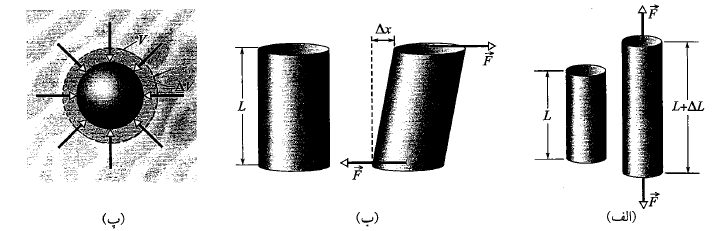
برش

وقتی شیئی تحت اثر تنش برشی قرار می گیرد معادله (6-1) می تواند به صورت زیر نوشته شود

(1-8)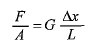

که در آن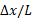 کرنش برشی شیء، 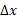جابه جایی یک سر شیء در جهت نیروی وارد شده 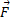( مطابق قسمت ب شکل فوق) و 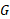مدول برشی است. تنش برابر با 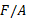 است.

تنش هیدرولیکی

وقتی به یک شیء تحت اثر تنش وارد شده از سوی شاره پیرامون تحت اثر تراکم هیدرولیکی اثر می کند معادله (6-1) می تواند به صورت زیر نوشته شود

(1-9)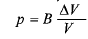

که در آن فشار ( تنش هیدرولیکی) وارد شده به شیء است که از شاره ناشی می شود،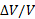 ( کرنش) مقدار مطلق تغییر حجم نسبی شیء ناشی از فشار و 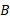مدول کپه ای شیء است.

مسئله نمونه- تنش و کرنش میله کشیده شده

یک سر میله فولادی به شعاع 9.5 میلیمترو طول  81 سانتیمتر را به گیره ای می بندیم. سپس به سر دیگر میله نیرویی به بزرگی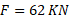 به طور عمود بر سطح مقطع میله ( به طور یکنواخت در سرتا سر سطح مقطع) وارد می کنیم و میله را در راستای دور شدن از گیره می کشیم. تنش وارد شده به این میله و افزایش طول 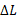و کرنش میله چقدر است؟

محاسبات: برای پیدا کردن تنش داریم

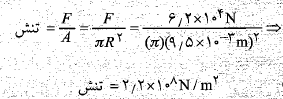
استقامت تسلیم مربوط به فولاد ساختمانی 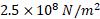 است. در نتیجه این میله به نحو خطرناکی به استقامت تسلیم خود نزدیک شده است. مقدار مدول یانگ مربوط به فولاد از جدول زیر داده شده است.

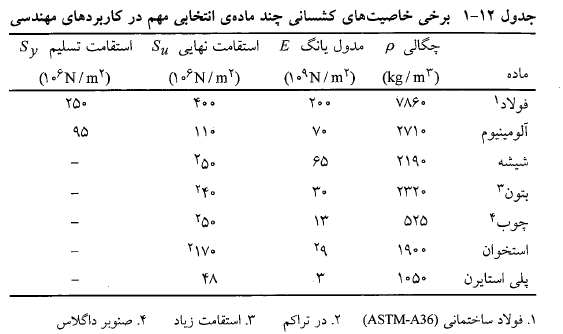
بنابراین افزایش طول از معادله (7-1) به  دست می آید

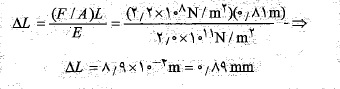
برای کرنش داریم

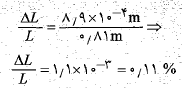
مسئله نمونه- توازن یک میز لق

طول هر یک از سه پایه یک میز 1 متر و طول پایه چهارم به اندازه  بلندتر است. در نتیجه میز اندکی لق می خورد. استوانه ای فولادی به جرم 290 کیلوگرم را به طور قائم روی این میز ( که جرمش خیلی کمتر از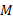 است) قرار می دهیم، به گونه ای که هر چهار پایه فشرده می شوند و میز به حال تراز می ماند و دیگر لق نمی خورد. پایه های میز استوانه هایی چوبی با مساحت مقطع 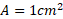هستند و مدول یانگ برابر است با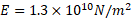. بزرگی نیروهای وارد شده به پایه های میز از سوی کف اتاق چیست؟

مجموع میز و استوانه فولادی را به عنوان دستگاه در نظر می گیریم. در این صورت وضعیتدستگاه مانند شکل زیر است، با این تفاوت که در اینجا استوان ای فولادی روی میز قرار گرفته است.

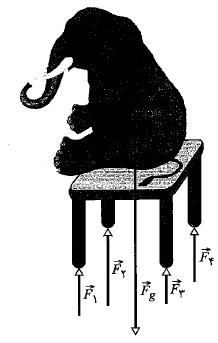
اگر سطح میز به حال تراز بماند پایه ها باید به صورت زیر متراکم شوند: هریک از پایه های کوتاه باید به مقدار مساوی ( در اینجا به اندازه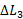) و با نیروی یکسان 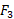متراکم شوند. تنها پایه بلند باید به مقدار بیشتر 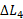و با نیروی بزرگ تر 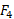متراکم شود. به عبارت دیگر برای یک میز تراز شده باید داشته باشیم

(1-10)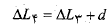

رابطه تغییر طول با نیروی به وجود آورنده این تغییر را می توان به صورت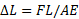 نوشت که در آن 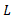طول اولی یک پایه است. با استفاده کردن از این رابطه می توان و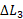  را در معادله (10-1) جانشانی کرد. اما توجه کنید که بطور تقریبی می توان طول اولی 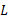هر چهار پایه را مساوی گرفت.

محاسبات: پس از جانشانی و تقریب زنی داریم

(1-11)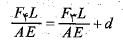

این معادله را نمی توان حل کرد چون دارای دو مجهول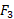 و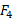 است. برای به دست آوردن معادله دیگری که شامل 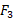و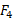 باشد می توان از محور قائم 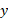استفاده کرد و معادله توازن نیروهای قائم 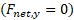را چنین نوشت

(12-1)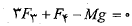

دراین رابطه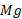 برابر با بزرگی نیروی گرانشی وارد شده به دستگاه است. ( به سه پایه نیروی 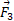وارد می شود). برای حل کردن هم زمان معادله های (11-1) و (12-1) به منظور تعیین مثلا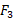، نخست از معادله (12-1) استفاده می کنیم و رابطه  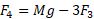را به دست می آوریم. با جانشانی این مقدار در معادله (11-1) و انجام دادن عملیات جبری لازم خواهیم داشت

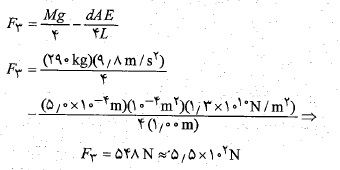
اکنون با استفاده کردن از معادله (12-1) داریم

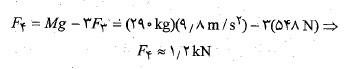
می توان نشان داد برای آنکه این پیکر بندی به حال تعادل برسد پایه های کوتاه به اندازه 0.44 میلیمتر و پایه بلند به اندازه 0.92 میلیمتر متراکم می شوند.

 برای مطالعه مباحث پیشرفته از محصول  دوره آموزشی فیزیک عمومی1 از سایت لینوم استفاده کنید