مشتق گیری
روش اول استفاده از چند جمله‌ای درون‌یاب هست. توی این روش این چندجمله‌ای رو که قبلا هم راجع بهش صحبت کردیم، به دست میاریم و ازش مشتق میگیریم. حاصل برای مشتق اول و دوم و با در نظر گرفتن جملات محدود به صورت زیر میشه. یک نکته‌ای هم که وجود داره اینه که این روش می‌تونه دقت خیلی کم و خطای خیلی زیادی داشته باشه!!!
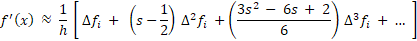
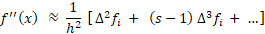
روند رسیدن به این معادله‌ها رو به صورت کامل داخلویدیو نشونتون دادیم.
حالا اگر بخوایم از فرمول‌های بالا برای محاسبه مشتق مرتبه اول و دوم در خود نقاط جدولی استفاده کنیم، 
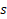رو باید چند بذاریم؟؟؟ اگر بخوایم از این فرمول در نقاط میانی ( نقاط وسط نقاط جدولی ) استفاده کنیم چی؟؟ سعی کنید برای این دو حالت چهار تا معادله‌ای که گفتیم رو بدست بیارید.
یک روش دیگه هم این هست که از بسط تیلور استفاده کنیم. اینجا رابطه‌های نهایی رو مینویسیم؛
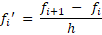
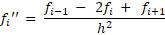
سعی کنید مشتق مرتبه اول رو بر اساس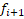
و 
بنویسید!!! اینجوری هر سه تا رابطه یک جورایی متقارن میشن...
حالا نوبتی هم که باشه، نوبت محاسبه خطای روش‌های مشتقگیری عددیه!!! برای محاسبه خطای مشتقگیری عددی مرتبه اول از روش بسط تیلور استفاده میکنیم... نتیجه نهایی یک همچین چیزی میشه:
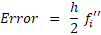
در حالت کلی خطا همیشه متناسب با توانی از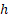
یا همون طول گام هست.
انتگرال‌گیری عددی
داخلویدیو یک سری مقدمه گفتیم راجع به اینکه، نحوه برخورد ما با یک انتگرال عددی به چه صورت هست و ایده اصلی کار چیه. پس اون ها رو رد میکنم و خیلی کوتاه راجع به روش ها صحبت میکنم.
اولین نکته اینه که باید بازه انتگرال مون رو به تعدادی زیر بازه تقسیم کنیم و مساحت زیر نمودار در هر کدوم از زیر بازه ها رو با یکی از روش‌ها تقریب بزنیم. واضحه که در نهایت مقدار عددی انتگرالمون برابر میشه با جمع همه این مساحت هایی که تقریب زدیم.
همون طور که گفتیم روش‌های مختلفی برای تقریب این مساحتها وجود داره... اسم اولیش روش ذوزنقه ای هست!!!
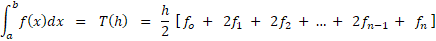
تقریبی از 
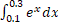را با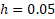
و به روش ذوزنقه‌ای محاسبه کنید.
روش ذوزنقه‌ای تابع تحت انتگرال رو در هر زیربازه به صورت درجه 1 (خط) تقریب میزنه. حالا اگر تابع رو در هر زیر بازه به صورت درجه 2 (سهمی) تقریب بزنیم، به روش دیگه‌ای می‌رسیم که اسمش روش سیمپسون هست. معادله این روش اینجوریه: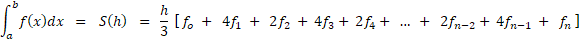 
یک روش خیلی مهم دیگه اسمش نیوتن– کاتس هست. معادلات این روش بر مبنای متساوی الفاصله بودن نقاط و صفر بودن خطا به ازای توابع تک جمله ای از توان هایx
به دست میاد. ما معمولا از ورژن چهار نقطه ای روش نیوتن– کاتس استفاده میکنیم. روش کار به این صورته که بازه انتگرال رو به 3 قسمت مساوی تقسیم میکنیم که از این تقسیم‌بندی چهار تا نقطه به وجود میاد که دوتاش همون کران های بالا و پایین انتگرال هستن. در ادامه باید از فرمول زیر استفاده بکنیم:
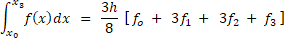
به این روش ضرایب مجهول هم میگن...
تقریبی از 
را به روش چهار نقطه‌ای نیوتن– کاتس محاسبه کنید.
اگر شرط متساوی الفاصله بودن رو قید نکنیم و معادلات بیشتری رو به تبع مجهولات بیشتر حل کنیم، ( این مراحل و محاسبات رو به صورت کامل در ویدیو انجام دادیم) به روشی می‌رسیم که اون رو با نام روش گاوس می‌شناسیم. اما ما این روش رو به دو حالت دو نقطه‌ای گاوس و سه نقطه‌ای گاوس محدود میکنیم. معادلات روش دو نقطه‌ای گاوس به این صورت هست:
و برای روش سه نقطه‌ای گاوس هم داریم:
نکته‌ای که وجود داره اینه که در هر دو این روش‌ها (دو نقطه ای و سه نقطه ای) کران پایین و بالای انتگرال به ترتیب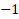
و
هستن!!! ولی خب انتگرال‌هایی که ما میگیریم لزوماً این جوری نیستن... چاره کار اینه که با یک تغییر متغیر خاص جوری تابع تحت انتگرالمون رو تغییر بدیم که کران‌های بالا و پایین بشن همونی که می‌خوایم.
کمی فکر کنید و سعی کنید روش و معادلات این تغییر متغیر رو خودتون به دست بیارید. کار سختی نیست... باور کنید!!!
آخرین روش اننگرال‌گیری عددی اسمش روش نقطه میانی هست. در این روش مساحت زیر نمودار تابع تحت انتگرال در هر زیر بازه به صورت مستطیلی تقریب زده میشه که عرضش همون طول گام هست و طول این مستطیل مقدار تابع، در نقطه وسط زیر بازه تقریب زده میشه. فرمول نهایی این روش اینه:
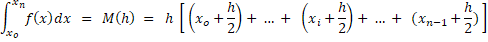
این روش به این دلیل که از نقاط سر و ته بازه انتگرال‌گیری هیچ استفاده‌ای نمیکنه، گزینه خیلی مناسبی برای محاسبه تقریبی و عددی انتگرال های منفرد هست.. فقط در همین حد بدونید که اگر تابع تحت انتگرال حتی در یکی از دو سر بازه انتگرال گیری تعریف نشده باشه، به اون انتگرال می‌گیم یک انتگرال منفرد.
همون طور که احتمالا حدس زدید، باز هم باید بریم سراغ مبحث خطایابی و دقت، که اینبار عنوانش میشه خطای روش‌ها و روابط انتگرال‌گیری تقریبی یا عددی...
قراره در مورد خطای سه تا از روش هایی که گفتیم بحث بکنیم. ولی چون اثبات های روابط به دست اومده طولانی هست و مطرح کردنش هم کمکی به حل سوالات نمیکنه، پس صرفا روابط خطا در این سه روش رو براتون آوردم.
این خطا ها رو باید بر حسب خطای مطلق بیان کنیم، یا خطای مطلق حدی؟؟؟
فرمول خطا در روش و رابطه ذوزنقه‌ای به این صورت هست:
برای روش سیمپسون فرمولمون اینجوریه:
و در آخر برای قاعده نقطه میانی داریم:
در روابط بالا منظور از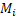
یعنی کران بالای مشتق مرتبه
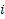ام تابع تحت انتگرال. یک نکته مهم دیگه اینه که نباید سر این مقدار ماکزیمم حساسیت به خرج بدیم... صرفا یک مقداری رو گزارش میکنیم که کاملا مطمئن باشیم مشتق مرتبه
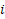ام تابع تحت انتگرال مون هیچوقت از اون بیشتر نمیشه و لازم نیست این مقدار خیلی دقیق باشه...
یک رابطه خیلی کارآمد که در به دست آوردن این مقدار ماکزیمم تقریبی کمکتون می‌کنه، نامساوی مثلثی هست که شکل متداول تر اون به این صورت نوشته میشه:
و ده ها نکته ناگفته دیگه که فقط توی مثال های خاص میشه دید...با مشاهده‌یویدیوهای محاسبات عددیمون کل پرسش‌‌های مطرح شده تو این مقاله‌ها رو می‌تونید پاسخ بدید.