درون‌یابی و برونیابی وقتی به دردمون می‌خوره که یک تابع رو به صورت جدولی داشته باشیم؛ یعنی یک سری نقاط محدودی از نمودار تابع رو به ما داده باشن. (مثلا یک سری نقاطی که به عنوان خروجی یک آزمایش فیزیکی گزارش شدن)
درون‌یابی یعنی بتونیم تابعی بنویسیم که از این نقاط بگذره، و به خاطر تابع بودنش بتونیم به ازای نقاطی که نداریم و بین این نقاط هستن، جواب تابع در اون نقاط رو به عنوان یک مقدار تقریبی گزارش کنیم.
حالا اگر مقدار تقریبی نقطه‌ای رو بیرون از بازه نقاط داده شده بخوایم، بهش میگیم برونیابی!!!
اولین روش اسمش روش چندجمله‌ای‌های لاگرانژ هست، که به وضوح مشخصه که لاگرانژ ارائه کرده این روش رو!!!
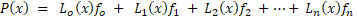
خب حالا این ضرایب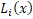
چی هستن؟؟؟
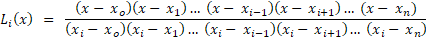
فرمول بالا رو امتحان کنید و ببینید که تمام نقاط جدولی توی این رابطه صدق میکنن!!!
سعی کنید سه تا عیب مهم روش لاگرانژ رو پیدا کنید و بنویسید.
اسم روش بعدی روش تفاضلات تقسیم شده نیوتنه...
فرمولای این روش رو میگیم، ولی یک روش خیلی آسون و سریع، داخلویدیوها گفته شده، که اگر ازش استفاده بکنید خیلی راحت میتونید به جواب برسید.
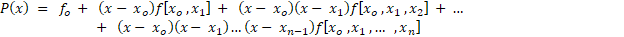
که توی این رابطه:
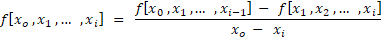
چهار تا نقطه از تابع 
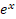به دلخواه انتخاب کنید و چند جمله ای درون‌یاب رو بر حسب دو روش لاگرانژ و نیوتن بنویسید.
تا اینجا دو روشی که گفتیم، حساسیتی روی فاصله بین نقاط تابع جدولی نداشتن، ولی روش بعدی فقط برای نقاط متساوی الفاصله قابل استفاده هست. اسم این روش تفاضلات پیشروئه... فرمول خود تفاضلات پیشرو مثل چند جمله‌ای‌های تقسیم شده نیوتن هست، با این تفاوت که مخرج کسر رو نداره... فقط صورت کسر هست!!!
چند جمله‌ای درون‌یاب بر اساس تفاضلات پیشرو به این صورته:
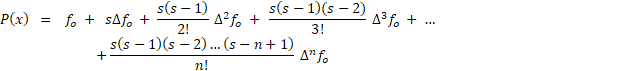
این ضرایب شما رو یاد چیز خاصی نمیندازه؟؟؟ یک مفهوم ترکیبیاتی مثلا...
دقت کنید که در روش بالا
اینه:
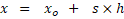
در واقع همه نقاط رو بر حسب نقاط متساوی الفاصله جدولی اینجوری مدل کردیم و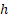
همون فاصله بین نقاط تابع جدولی، که بهش طول گام هم میگن، هست. پس تابع درون‌یاب بالا روآخر کار باید با یک تغییر متغیر به صورت تابعی از
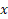نوشت.
چجوری تغییر متغیر بدیم؟؟؟ جای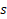 
چی بذاریم که 
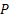تابعی از
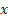بشه؟؟؟
یک تعریف دیگه هم داریم به نام تفاضل پسرو.. توی این روش از آخرین سطر جدول تفاضلات استفاده میشه. فرمولش هم اینجوریه:
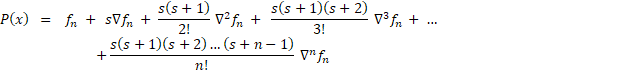
می‌رسیم به بحث شیرین خطا...فرمول خطای چند جمله‌ای‌های درون‌یاب یک همچین چیزیه:
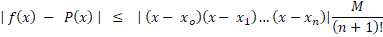
حالا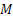
چیه؟؟؟
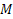کران بالای مشتق مرتبه
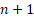ام تابع
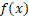در بازه
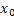تا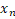 
هست!!!
حالا در مورد برونیابی... برون یابی فرقی با درون‌یابی نداره!!! کافیه از همون تابع درون‌یاب در نقاط خارج بازه استفاده کنیم. فقط حواستون باشه! خطای این کار خیلی زیاده... پس از این روش معمولا وقتی استفاده میشه که نقطه خارجی ما خیلی نزدیک یکی از دو انتهای بازه باشه.
یک روش دیگه اینه که نقطه مقدار خارج بازه رو با استفاده از رد کردن یک خط از دو نقطه انتهایی (یا ابتدایی) تابع جدولی و تقریب مقدار تابع در نقطه خارجی با استفاده از معادله این خط محاسبه کنیم!!! سعی کنید معادلات این نوع برونیابی خاص رو به دست بیارید.
و ده ها نکته ناگفته دیگه که فقط توی مثال‌های خاص میشه دید و شما اون‌ها رو میتونید توی ویدیوهامون ببینید...
برای بررسی بیشتر این درس پیشنهاد میکنیم که کپسول آموزشی محاسبات عددی ما رو از لینک زیر ببینین :