4) معرفی انتگرالهای توابعمختلط و روش حل انتگرالهایتوابع مختلط

در اینآموزش کپسولی لینوم به معرفی انتگرالتابعمختلط و بررسی خواص آن میپردازیم. این کار با استفاده از انتگرال روی منحنی در داخل صفحه انجام میپذیرد. بااستفاده از آن نشانخواهیمداد هر تابعتحلیلی روی منحنی در داخل صفحه انجاممیپذیرد. بااستفاده از آن نشانخواهیمداد هر تابع تحلیلی نه تنها بینهایت بار مشتقپذیر است بلکه دارای بسط تیلور نیز میباشد. با استفاده از این نتایج، محاسبه انتگرالهایمعین پیچیده حقیقی به سادگی و میتوان گفت در حد انجام محاسبات چهار عمل اصلی قابل انجام است. مثلا انتگرالهای زیر به سادگی قابل محاسبه هستند:
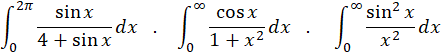
قضیه کوشی-گورسای یا قضیه انتگرال کوشی و نتایج آن مهمترین مطلب مبحث انتگرال خواهدبود. با نتایج حاصل محاسبه انتگرالهای فوق مقدور میگردد. خواهیمدید معرفی سری تیلور و سری مک-لورن محاسبه انتگرالهای مختلط را سادهتر میکنند و نهایتا با معرفی مانده و خواص آن کار محاسبات را در حد محاسبات چهار عمل اصلی تقلیل میدهیم.
1-4 انتگرالمختلط و روشهای حل آن
برای معرفیانتگرال در ابتدا به یادآوری مفاهیمی از منحنی در صفحه میپردازیم. هر تابع پیوسته مانند 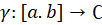 را یک منحنی در صفحه مختلط یا مختصرا یک منحنی گوییم. این منحنی را به صورت پارامتری زیر میتوان نمایشداد.
را یک منحنی در صفحه مختلط یا مختصرا یک منحنی گوییم. این منحنی را به صورت پارامتری زیر میتوان نمایشداد.
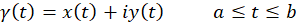
که در آن 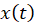 و
و 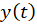 توابع حقیقی از متغییر حقیقی
توابع حقیقی از متغییر حقیقی 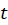 است.
است.
 مثال1)منحنی
مثال1)منحنی 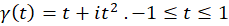 همان منحنی
همان منحنی 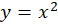 با دامنه
با دامنه 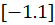 است.
است.
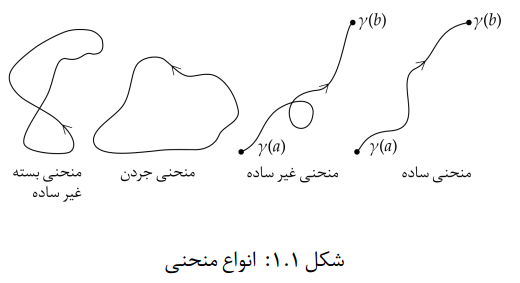
منحنی 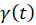 را یک منحنی ساده گوییم اگر خودش را قطع نکند. این منحنی را بسته گوییم اگر نقاط ابتدا و انتهای آن بر هم منطبق باشند. یعنی
را یک منحنی ساده گوییم اگر خودش را قطع نکند. این منحنی را بسته گوییم اگر نقاط ابتدا و انتهای آن بر هم منطبق باشند. یعنی 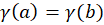 . منحنی بسته و ساده را منحنی جردن گویند. (شکل1.1) اگر طول منحنی متناهی باشد، آن را با طول متناهی گویند. جهت منحنی را جهت افزایش
. منحنی بسته و ساده را منحنی جردن گویند. (شکل1.1) اگر طول منحنی متناهی باشد، آن را با طول متناهی گویند. جهت منحنی را جهت افزایش 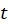 بر روی آن میگیریم. جهت منحنی را جهت مثلثاتی روی دایره و در داخل آن میگیریم. این جهت را جهت مثبت منحنی جردن و خلاف آن را جهت منفی میدانیم.
بر روی آن میگیریم. جهت منحنی را جهت مثلثاتی روی دایره و در داخل آن میگیریم. این جهت را جهت مثبت منحنی جردن و خلاف آن را جهت منفی میدانیم.
تعریف انتگرال مختلط
فرض کنید 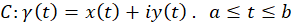 یک منحنی در صفحه و
یک منحنی در صفحه و 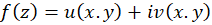 یک تابع پیوسته با دامنه
یک تابع پیوسته با دامنه 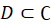 باشد، به طوری که منحنی
باشد، به طوری که منحنی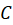 در داخل
در داخل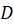 واقع باشد، انتگرال
واقع باشد، انتگرال 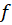 روی
روی 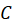 را که با
را که با 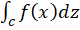 نشان میدهیم به صورت زیر تعریف میکنیم:
نشان میدهیم به صورت زیر تعریف میکنیم:
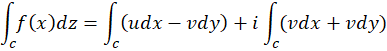
 مثال2) مطلوبست محاسبه
مثال2) مطلوبست محاسبه 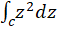 که در آن
که در آن 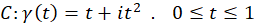 .
.
حل:
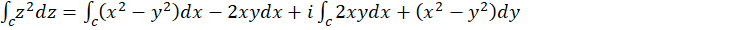
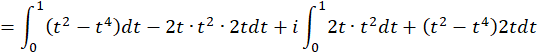
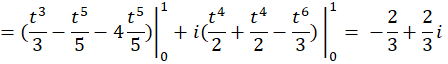
**تذکر
برای بازنویسی تعریف فوق کافیست در 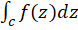 به جای
به جای 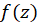 مقدار
مقدار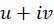 و به جای
و به جای 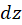 مقدار
مقدار 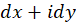 را قراردهیم و ساده کنیم:
را قراردهیم و ساده کنیم:
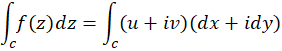
در زیر خواصی از انتگرال را میآوریم که برای انتگرال روی منحنی برقراراست. در این جا فرض بر این است که که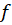 و
و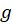 توابع مختلط پیوسته و
توابع مختلط پیوسته و 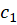 و
و 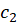 و
و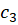 منحنیهای با طول متناهی هستند.
منحنیهای با طول متناهی هستند.
1- از انتگرال روی منحنی داریم:
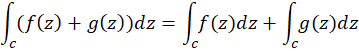
2- برای هر عدد مختلط 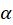 داریم:
داریم:
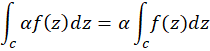
3- اگر 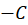 منحنی
منحنی 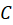 در جهت عکس باشد، آنگاه:
در جهت عکس باشد، آنگاه:
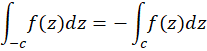
4- اگر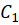 و
و 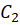 دو منحنی در صفحه و ابتدای
دو منحنی در صفحه و ابتدای 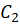 بر انتهای
بر انتهای 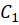 منطبق باشد، آنگاه:
منطبق باشد، آنگاه:
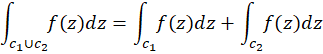
5- اگر منحنی 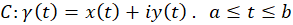 دارای مشتق قطعهبهقطعه پیوسته هموار باشد، آنگاه:
دارای مشتق قطعهبهقطعه پیوسته هموار باشد، آنگاه:
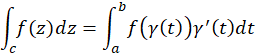
6- اگر منحنی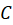 دارای دو نوع نمایش پارامتری متفاوت مانند
دارای دو نوع نمایش پارامتری متفاوت مانند 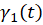 و
و 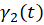 باشد، آنگاه:
باشد، آنگاه:
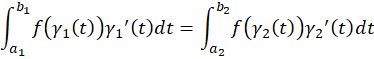
یعنی مقدار انتگرال به نحوه پارامتری کردن منحنی 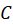 بستگی ندارد.
بستگی ندارد.
7- اگر منحنی 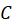 دارای طولی برابر
دارای طولی برابر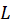 و برای نقاط
و برای نقاط 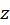 روی منحنی
روی منحنی 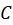 داشتهباشیم
داشتهباشیم 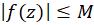 ،
، 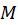 عددی ثابت، آنگاه:
عددی ثابت، آنگاه:
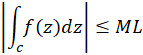
8- فرضکنید 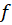 و
و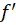 روی
روی 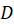 پیوسته و
پیوسته و 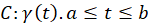 با
با 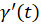 قطعهبهقطعه پیوسته در داخل
قطعهبهقطعه پیوسته در داخل 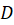 باشد، آنگاه:
باشد، آنگاه:
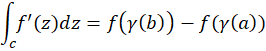
این خاصیت را میتوان تعمیمی از قضیه اساس حسابدیفرانسیل و انتگرال دانست.
 مثال3)مطلوبست محاسبه
مثال3)مطلوبست محاسبه 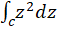 ، وقتی
، وقتی 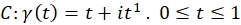 .
.
حل: با توجه بهویژگی5مینویسیم:
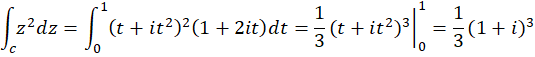
4-2 قضیه کوشی و نتایج آن

اکنون به بیان قضیه انتگرال کوشی که به قضیه کوشی-گورسای نیز شهرت دارد میپردازیم. این قضیه همان قضیه گرین برای توابع مختلط است که اساس نظریه توابع مختلط است.
قضیه کوشی: اگر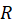 یک حوزه همبند(ساده یا مرکب) با مرز
یک حوزه همبند(ساده یا مرکب) با مرز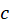 قطعهبهقطعه هموار باشد و
قطعهبهقطعه هموار باشد و 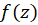 روی و داخل
روی و داخل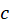 ، تحلیلی باشد، آنگاه:
، تحلیلی باشد، آنگاه:
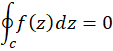
(این خاصیت، معادل دیفرانسیل کامل بودن 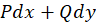 در انتگرالهای حقیقی است.)
در انتگرالهای حقیقی است.)
 مثال4)
مثال4) 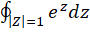 را محاسبه کنید.
را محاسبه کنید.
حل: تابع 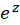 یک تابع تام است، پس درون و روی دایره واحد تحلیلی است. بنابراین مقدار انتگرال صفر است.
یک تابع تام است، پس درون و روی دایره واحد تحلیلی است. بنابراین مقدار انتگرال صفر است.
از قضیه کوشی نتابج زیر حاصل میشود:
1- در هر حوزه همبند ساده که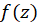 در آن تحلیلی است،
در آن تحلیلی است، 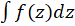 مستقل از مسیرانتگرالگیری است.
مستقل از مسیرانتگرالگیری است.
2- اگر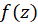 در حوزه
در حوزه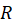 تعریف شده و
تعریف شده و 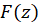 در این ناحیه تحلیلی باشد، همچنین در این حوزه داشتهباشیم
در این ناحیه تحلیلی باشد، همچنین در این حوزه داشتهباشیم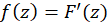 ، آنگاه
، آنگاه 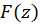 یک تابع اولیه
یک تابع اولیه 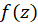 است. حال اگر
است. حال اگر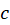 یک خم ساده بین دو نقطه
یک خم ساده بین دو نقطه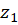 و
و 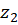 واقع در
واقع در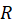 باشد، در اینصورت داریم:
باشد، در اینصورت داریم:
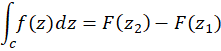
به عبارت دیگر اگر مشتق یک تابع تحلیلی باشد، در این صورت انتگرال آن مستقل از مسیر انتگرالگیری است و میتوان از آن مستقیما انتگرال گرفت. به خصوص اگر ، در این صورت مقدار انتگرال صفر است. (قضیه کوشی)
3- اگر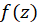 داخل و روی مرز حوزه
داخل و روی مرز حوزه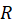 ، ناحیه بین دو منحنی بسته ساده غیرمتقاطع
، ناحیه بین دو منحنی بسته ساده غیرمتقاطع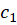 و
و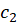 جهتدار در جهت مثبت، تحلیلی باشد آنگاه:
جهتدار در جهت مثبت، تحلیلی باشد آنگاه:
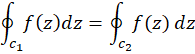
4- اگر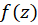 داخل و روی مرز ناحیه
داخل و روی مرز ناحیه 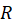 ، ناحیه بین منحنیهای بسته ساده غیرمتقاطع
، ناحیه بین منحنیهای بسته ساده غیرمتقاطع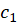 ،
،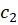 ، .... ،
، .... ، 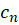 و
و جهت دار در جهت مثبت، (مطابق شکل بالا) تحلیلی باشد، آنگاه:
جهت دار در جهت مثبت، (مطابق شکل بالا) تحلیلی باشد، آنگاه:
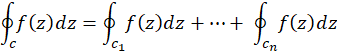
 مثال5) مقدار
مثال5) مقدار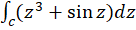 ، که در آن
، که در آن 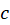 بخشی از سهمی
بخشی از سهمی 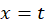 ،
، 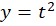 ، برای
، برای 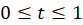 است را محاسبهکنید.
است را محاسبهکنید.
حل: تابع 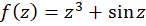 یک تابع تام است، پس در هر ناحیه شامل خم فوق تحلیلی است، پس انتگرال آن مستقل از مسیر است و داریم:
یک تابع تام است، پس در هر ناحیه شامل خم فوق تحلیلی است، پس انتگرال آن مستقل از مسیر است و داریم:
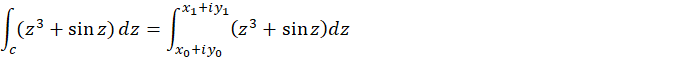
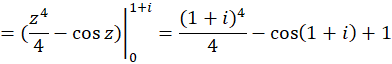
5-2 قضیه انتگرال کوشی و نتایج آن
قضیه انتگرال کوشی روش محاسبه 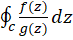 را وقتی
را وقتی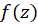 در داخل ناحیه انتگرالگیری تحلیلی است و
در داخل ناحیه انتگرالگیری تحلیلی است و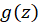 یک چند جملهای است که حداقل یک صفر آن در داخل ناحیه انتگرالگیری واقع است، توضیح میدهد.
یک چند جملهای است که حداقل یک صفر آن در داخل ناحیه انتگرالگیری واقع است، توضیح میدهد.
قضیه انتگرال کوشی- اگر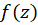 در داخل و روی مرز
در داخل و روی مرز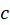 یک ناحیه همبند ساده
یک ناحیه همبند ساده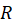 ، تحلیلی بوده و
، تحلیلی بوده و 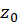 یک نقطه داخلی باشد، آنگاه:
یک نقطه داخلی باشد، آنگاه:
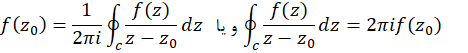
قضیه انتگرال کوشی-اگر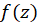 روی حوزه همبند ساده
روی حوزه همبند ساده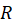 و مرز آن
و مرز آن 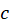 تحلیلی باشد، در اینصورت تمام مشتقات مراتب مختلف
تحلیلی باشد، در اینصورت تمام مشتقات مراتب مختلف 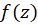 در نقطه داخلی
در نقطه داخلی 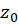 از
از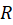 موجود بوده و تحلیلی میباشند و داریم:
موجود بوده و تحلیلی میباشند و داریم:
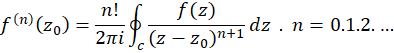
به عبارت دیگر یک تابع تحلیلی نه فقط تمام مشتقات از همه مراتب را داراست، بلکه هر مشتق خود یک تابع تحلیلی است، زیرا دارای مشتق است. این خاصیت برای توابع حقیقی برقرار نیست و آنها میتوانند فقط دارای چند مشتق در یک نقطه بوده و فاقد مشتقات مراتب بالاتر در آن نقطه باشند، به عنوان مثال 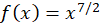 از مشتق چهارم به بعد را در نقطه
از مشتق چهارم به بعد را در نقطه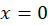 دارا نیست.
دارا نیست.
 مثال6)فرضکنید
مثال6)فرضکنید 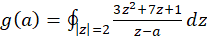 ؛ مقادیر
؛ مقادیر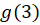 ،
، 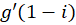 و
و 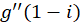 را تعیین کنید.
را تعیین کنید.
حل:
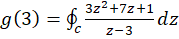
چون نقطه 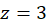 خارج دایره واقع است، بنابراین
خارج دایره واقع است، بنابراین 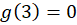 .
.
داریم 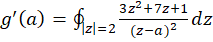 ، پس
، پس 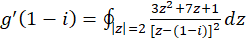 .
.
چون 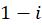 در داخل خم است با استفاده از فرمول انتگرال کوشی نتیجه میگیریم:
در داخل خم است با استفاده از فرمول انتگرال کوشی نتیجه میگیریم:
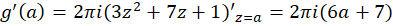
در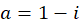 ، داریم
، داریم 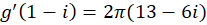 . به همین طریق میتوان نشان داد که چون
. به همین طریق میتوان نشان داد که چون 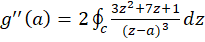 ، پس:
، پس:
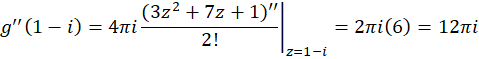
نتایج قضیه انتگرال کوشی
با استفاده از فرمول انتگرال کوشی نتایج مهمی حاصل میشود. ما در زیر به ذکر مهمترین آنها میپردازیم:
1- قضیه مُررا (عکس قضیه کوشی):اگر 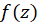 در حوزه ساده
در حوزه ساده 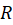 پیوسته بوده و برای هر منحنی
پیوسته بوده و برای هر منحنی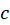 در این ناحیه
در این ناحیه 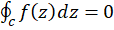 باشد، آنگاه
باشد، آنگاه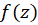 در
در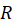 تحلیلی است.
تحلیلی است.
2- نامساوی کوشی:اگر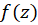 روی و داخل دایره
روی و داخل دایره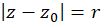 تحلیلی بوده و
تحلیلی بوده و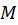 کرانی برای
کرانی برای 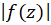 روی
روی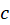 باشد، در این صورت چون:
باشد، در این صورت چون:
برای یادگیری بیشتر مبحث انتگرال، میتوانیدویدیو آموزشی انتگرال را مشاهده کنید.