معادلات دیفرانسیل خاص

1-معادله دیفرانسیل لژاندر

2-معادله دیفرانسیل بسل

معادله دیفرانسیل لژاندر

 

تعریف

فرم کلیمعادله دیفرانسیل لژاندر به شکل زیر است:

1-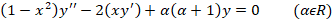      

روش حل معادلات دیفرانسیل لژاندر

در مسائل مختلف غالبا جواب این معادله حول نقطه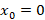 پرسیده میشود پس ما هم به بررسی جوابمعادله لژاندر حول این نقطه می پردازیم.با توجه به این که 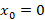یک نقطه عادی برای این معادله است پس جواب این معادله را 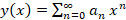فرض می کنیم.با توجه به روش هایی که پیش از این به آن ها اشاره شد به تعیین ضرایب 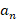می پردازیم و نهایتا فرم نهایی جوای معادله لژاندر به صورت زیر بدست می آید:

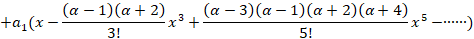
که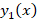 برابر است با:

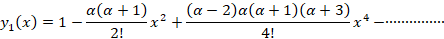
و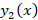 به صورت زیر است:

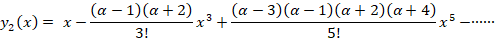
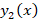دو تابع و را توابع لژاندر می نامند.

در صورتی که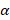 عددی طبیعی نباشد هر دو تابعی که جواب را تشکیل می دهند به فرم سری نا متناهی هستند ولی اگر عددی طبیعی باشد یکی از توابع به صورت چند جمله ای از درجه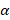 خواهد بود و تابع دیگر همچنان به صورت سری نامتناهی.تابعی از جواب را که به صورت چند جمله ای باشد ، چندجمله ای لژاندر می نامیم.

اگر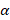 عددی زوج باشد 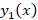به صورت چندجمله ای از درجه 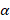خواهد بود و اگر 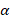عددی فرد باشد 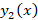به صورت چندجمله ای از درجه 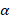خواهد بود.چند جمله ای هایلژاندر به ازای 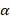های زوج تابعی زوج و به ازای 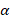های فرد تابعی فرد هستند.

مثال: یک جواب معادله دیفرانسیل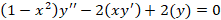 را بدست آورید.

ابتدا را تعیین می کنیم:

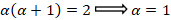
یک جواب این معادله چند جمله ای از درجه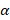 است و با توجه به مقدار پس آن جواب چند جمله ای درجه اول است:

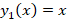
فرمول رودریگز

چند جمله ای های لژاندر را می توان از طریق رابطه زیر که فرمول رودریگز نامیده می شود بدست آورد:

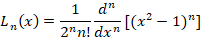
مفید خواهد بود اگر جملات ابتدایی چند جمله ای لژاندر را به خاطر داشته باشید:

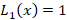
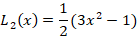
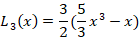
تعامد چند جمله ای های لژاندر

چند جمله ای های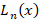 در بازه دو به دو بر هم عمودند:

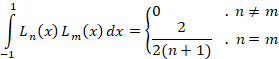
قضیه

بسط لژاندر

اگر تابع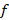 تابعی هموار بر بازه بسته باشد در این صورت این تابع را می توان بر حسب چند جمله ای های لژاندر بسط داد.در واقع میتوان نوشت:

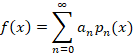
که در آن:

 

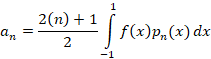
مثال: سه ضریب بسط لژاندر تابع   را بیابید.

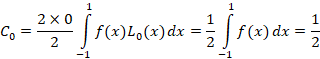
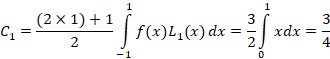
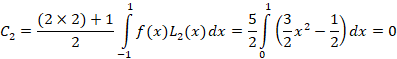
پس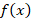 به صورت زیر خواهد بود:

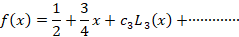
مثال: اگر  و 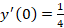  چهار جمله اول معادله 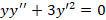را به کمک سری حول نقطه 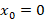بدست آورید.

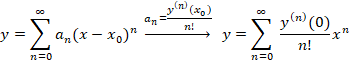
چهار جمله اول معادله به فرم زیر است:

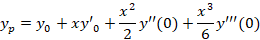
حال باید پارامترهای عبارت فوق را تعیین کنیم.ابتدا با جایگذاری در معادله اصلی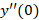 را بدست می آوریم:

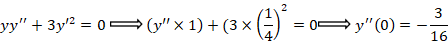
و بامشتق گیری از معادله اصلی و جایگذازی مقادیر بدست آمده در آن مقدار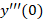 برابر خواهد بود با:

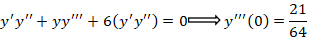
و در نهایت چهارجمله اول جواب معادله مطابق با مقادیر زیر است:

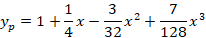
رابطه بازگشتی چند جمله ای های لژاندر

رابطه بازگشتی زیر برای چند جمله ای های لژاندر برقرار است:

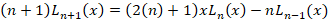
تابع گاما

 

تعریف

تابع گاما به صورت زیر برای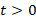 بیان می شود:

روابط تابع گاما

دو رابطه زیر برایتابع گاما برقرار است:

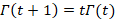
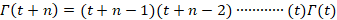
معادله دیفرانسیل بسل

 

تعریف

فرم کلی معادله دیفرانسیل بسل به صورت زیر است:

     

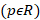
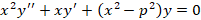
روش حل معادله دیفرانسیل بسل

نقطه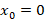 یک نقطهتکین منظم برای معادله دیفرانسیل بسل است و موضوع مورد اهمیت برای ما هم جواب این معادله حول همین نقطه است.با حل این معادله یکی از جواب های آن به صورت زیر بدست خواهد آمد:

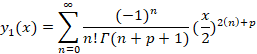
عبارت بدست آمده را تابع بسل نوع اول می نامند و آن را با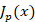 نشان می دهند.جواب دیگر معادله از طریق رابطه آبل به شکل زیر بدست می آید:

و در نهایت جواب عمومی معادله نیز برابر است با:

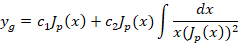
روابط کاربردی در تابع بسل

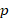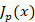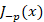1-با توجه به این که به ازای های غیر صحیح و مستقل خطی هستدجواب عمومی معادله بسل مرتبه 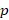به ازای 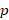های غیر صحیح به شکل زیر است:

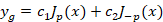
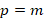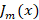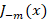2-اگر عددی صحیح باشد در این صورت و  مستقل خطی نیستند و رابطه زیر بین آن ها برقرار است:

 

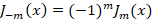
دراین حالت جواب دوم معادله را میتوان از طریق فرموال آبل بدست آورد که به فرم زیر است:

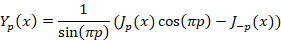
که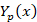 را تابع بسل نوع دوم یا تابع نیومان می نامیم.

3-برخی از معادلات در ابتدا فرم معادلات بسل را ندارند ولی با تغییر متغیر می توان آن ها را به معادلات بسل تبدیل کرد.

خواص تابع بسل نوع اول

تابع بسل نوع اول دارای خواصی می باشد که در حل مسائل بسیار کاربردی می باشند و بهتر است آن ها را در خاطر داتشه باشید:

1-

2-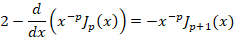

3-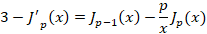

4-

5-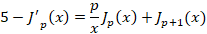

6-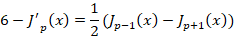

7-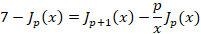

8-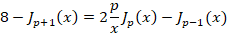

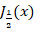مثال: مقدارJ12(x) را محاسبه نمایید.

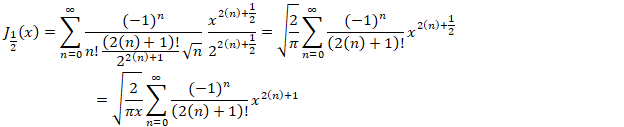
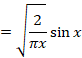
بسط توابع بسل

اگر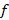 و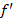 تنها و تنها دارای تعداد متناهی نقطه ناپیوستگی باشند در این صورت برای هر 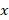که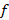 در آن پیوسته است داریم:

که در آن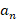 به صورت زیر محاسبه می شود:

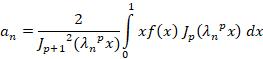
مثال: تابع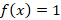 را بر اساس خانواده توابع  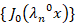 بسط دهید.

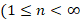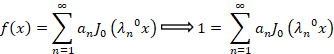
با توجه به رابطه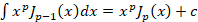 که پیش از این به آن اشاره کرده بودیم داریم:

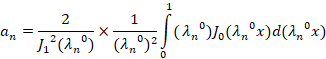
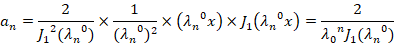
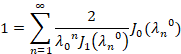
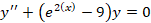مثال: معادله را حل کنید.

برای حلمعادله دیفرانسیل فوق بادی از تغییر متغیر  استفاده کنیم تا به یک معادله بسل برسیم و در نهایت به سادگی حل شود:

---

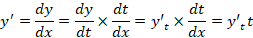
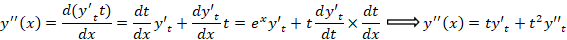
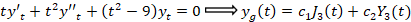
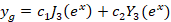
برای تسلط بیشتر بر این مباحث، می‌توانید  کپسول آموزشی معادلات دیفرانسیللینوم را  مشاهده کنید.