سری فروبنیوسی
اگر بخواهیممعادله را حول یک نقطه منفرد منظم حل کنیم میتوانیم از سری فروبنیوسی استفاده کنیم.اگرx0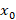
یک نقطه منفرد منظم برای معادله y''+pxy'+qxy=0
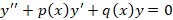باشد آنگاه دو رابطه زیر برقرار است:
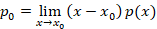
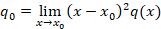
و نتیجتا معادله مشخصهمعادله دیفرانسیل فوق برابر است با:
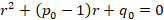
اکنون با توجه به ریشه های معادله مشخصه فوق با یکی از حالات زیر روبرو خواهیم شد:
1-اگرr1>r2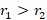
دو ریشه حقیقی برای معادله مشخصه باشند و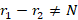
در این صورت معادله دارای دو جواب به فرم زیر است:
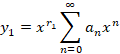
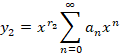
توجه کنید که ضرایب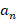
در دو عبارت فوق دارای مقادیر متفاوت هستند.نهایتا هم جواب عمومی به صورت زیر خواهد بود:
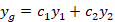
2-اگر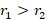
دو ریشه حقیقی برای معادله مشخصه باشند و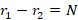
در این حالت یک جواب معادله به صورت زیر خواهد بود:
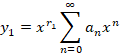
و برای یافتن جواب دیگر ازفرمول آبل استفاده می کنیم.بعد از بدست آمدن جواب دوم جواب عمومی معادله به صورت زیر خواهد بود:
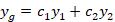
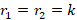ریشه مضاعف معادله مشخصه باشد
اگر معادله مشخصه دارای ریشه مضاعف به صورت فوق باشد یکی از جواب های معادله به فرم زیر است:
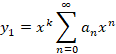
جواب دیگر این معادله نیز مانند حالت دو از فرمول آبل بدست می آوریم.جواب عمومی این معادله برابر است با:
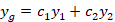
توجه: اگر از سری های فروبنیوسی مشتق بگیریم اندیس پایین همان صفر باقی خوهاد ماند.
مثال: جواب معادله دیفرانسیل
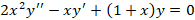را حول
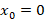بدست آورید.
با توجه به روابطی که پیش از این به آن ها اشاره شده است متوجه می شویم که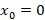
یک نقطه منفرد منظم برایمعادله دیفرانسیل است و در ادامه داریم:
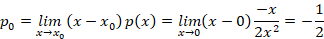
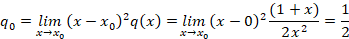
توجه کنید که برای استفاده از این دو رابطه باید ابتدا معادله را به فرم کانونی بازنویسی کنید.با توجه به مقادیر بدست آمده معادله مشخصه به شکل زیر است:
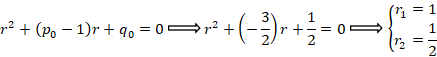
با توجه به این که معادله دو ریشه دارد ، r1>r2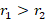
وr1-r2≠N
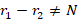پس با حالت اول روبرو هستیم:
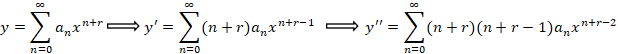
در معادله قرار می دهیم:
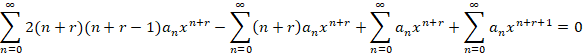
نکته مهمی که باید به آن توجه داشته باشید این است که گاها برای حل معادله نیاز بهتغییر اندیس سیگما ها هستید و در نتیجه این عمل عبارات درون سیگما نیز دچار تغییراتی می شوند به طور مثال برای حل معادله فوق باید اندیس عبارت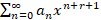
را تغییر دهیم که به شکل زیر صورت می پذیرد:
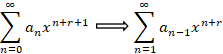
در ادامه معالده فوق به صورت زیر تبدیل می شود:
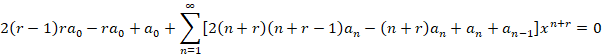
حال باید ضریب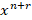
را صفر قرار دهیم:
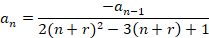
اکنون با توجه به دو مقدار متفاوت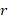
دو سری جواب متفاوت داریم.ایتدا سری جواب مربوط به
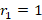را بدست می آوریم:
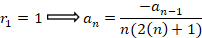
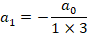
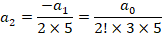
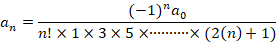
و جواب اول معادله به فرم زیر خواهد بود:
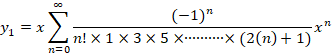
جواب دیگر معادله را نیز به همین ترتیب به ازای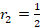
به شکل زیر بدست می آوریم:
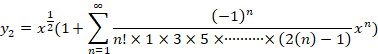
و نهایتا جواب عمومی معادله برابر است با:
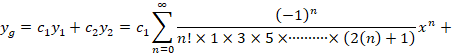
c2x(1+n=1∞-1nn!×1×3×5×∙∙∙∙∙∙∙∙∙∙×2n-1xn)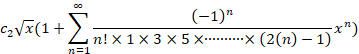
مثال: معادله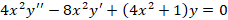
را حول نقطه
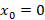حل کنید.
با بررسی هایی که قبلا به توضیح آن ها پرداختیم می توانیم متوجه شویم که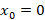
یک نقطه منفرد منظم است پس داریم:
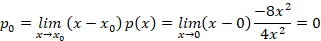
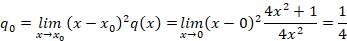
توجه کنید که برای استفاده از این دو رابطه باید ابتدا معادله را به فرم کانونی بازنویسی کنید.با توجه به مقادیر بدست آمده معادله مشخصه به شکل زیر است:
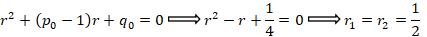
با توجه به این موضوع که r1=r2=k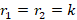
و معادله دارای ریشه مضاعف است پس با حالت سوم روبرو هستیم:
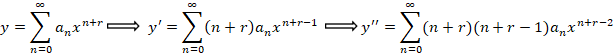
در معادله قرار می دهیم:
بعضی از عبارات باید به ترتیب زیر تغییر اندیس داده شوند:
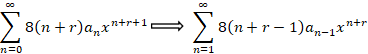
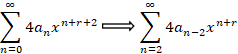
در ادامه معادله فوق به صورت زیر تبدیل می شود:
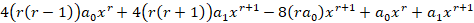
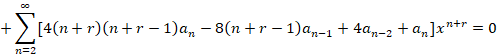
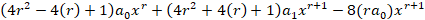
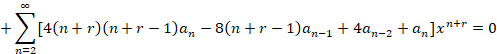
صفر قرار دادن ضریبxr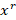
مقدار همانr
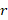را به می دهد که پیش از انی بدست آوردیم و به آن نیازی نداریم اما با صفر قراردادن ضرایب
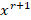و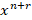
به ترتیب داریم:
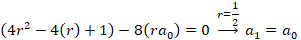
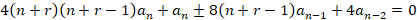
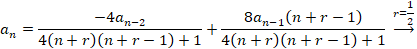
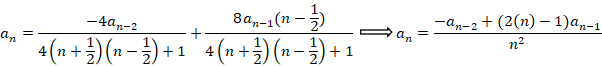
حالا باید سری جواب را بدست آوریم:
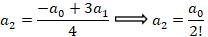
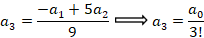
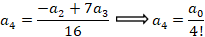
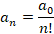
و جواب اول معادله به فرم زیر خواهد بود:
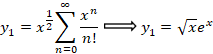
اکنون جواب دوم معادله را با استفاده ازفرمول آبل بدست می آوریم:
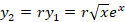
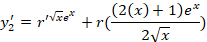
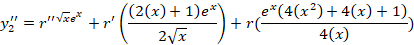
با جایگذاری در معادله جواب دوم به فرم زیر بدست خواهد آمد:
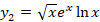
و نهایتا جواب عمومی معادله برابر است با:
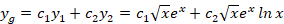
برای تسلط بیشتر بر این مباحث، می‌توانید کپسول آموزشی معادلات دیفرانسیل لینوم را مشاهده کنید.