استقلال و وابستگی خطی
در این آموزش معادلات دیفرانسیل لینوم، به سراغ یادگیریاستقلال و وابستگی خطی و روش حل معادلات دیفرانسیل مرتبه دوم می‌رویم.
توابع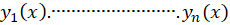
را در بازه
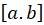مستقل خطی می‌گوییم هر گاه به ازای هر
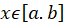، رابطة زیر نتیجه دهد
:
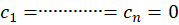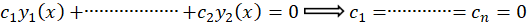
اگر بخواهیم تعریف فوق را در حالت خاص دو تابع بررسی کنیم باید بگوییم توابع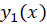
و
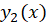را در بازه
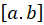مستقل خطی می‌گوییم هر گاه به ازای هر 
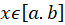، رابطة زیر در صورتی برقرار باشد که
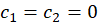، در غیر این صورت 
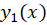و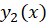
وابسته خطی هستند.
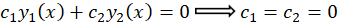
اگر دو تابع را بر هم تقسیم کنیم و خارج قسمت آن‌ها عدد ثابتی شود آن دو تابع وابسته خطی هستند و در غیر این صورتمستقل خطی هستند.
رونسکین
اگر دو تابع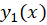
و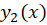
در نقطه 
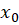مشتق‌پذیر باشندرونسکین این دو تابع را به صورت زیر تعریف می‌کنیم:
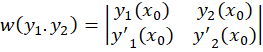
اگر رونسکین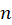
تابع در نقطه 
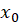را نیز بخواهیم حساب کنیم کافیست دترمینان ماتریس با مرتبه
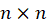را مشابه بالا را حساب کنیم.
قضیه: دو تابع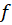
و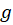
مستقل خطی هستند اگر و تنها اگر
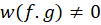باشد.
مثال) استقلال خطی دو تابع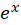
و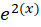
را با توجه بهرونسکین آن‌ها بررسی نمایید.
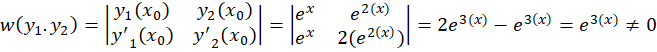
پس این دو تابع مستقل خطی هستند.
قضیه: اگر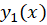
و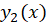
دو جواب از معادله دیفرانسیل
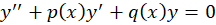باشند آنگاهرونسکین این آن‌ها یا همواره صفر است یا همواره نا صفر و به شکل زیر به‌دست می‌آید:
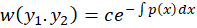
روش حل معادلات دیفرانسیل مرتبه دوم
توجه کنید که این دسته از معادلات در حالات خاصی قابل حل است و ما در ادامه به انواع آن‌ها و روش حل آن‌ها خواهیم پرداخت:
روش کاهش مرتبه
اگر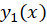
جوابی برایمعادله دیفرانسیل
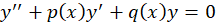باشد ، جواب دوم معادله مذکور که مستقل خطی با
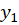باشد را می توان به صورت
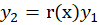در نظر گرفت که با جایگذاری در معادله داریم:
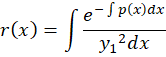
رابطه فوق رافرمول آبل می‌نامند و با استفاده از آن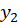
به‌دست می‌آید و با توجه به قضیه‌ای که پیش از این توضیح داده شد جواب عمومی معادله برابر با ترکیب خطی
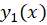و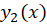
می‌باشد.
نکته حائز اهمیت در روش کاهش مرتبه این است که حتما باید یک جواب از معادله را داشته‌باشیم.
مثال) اگر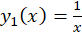
یکی از جواب‌های معادله
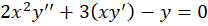باشد، جواب عمومی معادله را به‌دست آورید.
ابتدا معادله را باید به شکل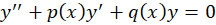
در آوریم پس با تقسیم طرفین بر
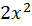داریم:
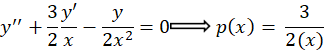
اکنون از فرمول آبل استفاده می‌کنیم:
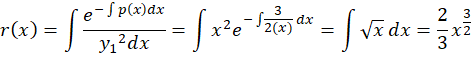
با توجه به این که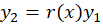
داریم:
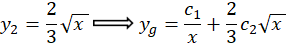
معادلات مرتبه دوم خطی همگن با ضرایب ثابت
فرم کلی این معادلات به صورت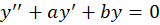
است و یک جواب این معادله قطعا به فرم
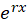می‌باشد.
روش حل معادلات مرتبه دوم خطی همگن با ضرایب ثابت
برای حل این معادلات ابتدا باید مقدار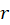
را با حل معادلهr2+ar+b=0
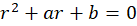بدست آوریم.این معادله رامعادله مفسر یا مشخصه می‌نامند.
برای حل این معادله با توجه به مقدار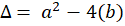
ممکن است با سه شرایط مختلف روبرو شویم:
1-اگر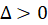
باشد ، دو ریشهr1
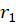وr2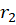
داریم و دو جواب مستقل خطی معادله دیفرانسیل ما به صورت
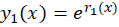و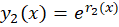
است و جواب عمومی معادله برابر است با:
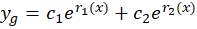
2-اگر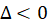 
باشد ، معادله مشخصه دارای دو ریشه مختلط است که به صورت
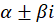هستند.با توجه به این موضوع می‌توانیم دو جواب مستقل خطی از معادله دیفرانسیل را هم داشته باشیم که به صورت
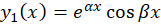و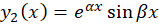
هستند.جواب عمومی معادله نیز برابر است با:
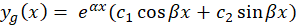
3-اگر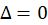
باشد، معادله مفسردارای ریشه مضاعف است و مقدار آن برابر است با 
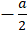. یکی از جواب‌هایمعادله دیفرانسیل برابر است با
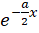. برای به‌دست آوردن یک جواب دیگر از معادله از روش کاهش مرتبه استفاده می‌کنیم و به این ترتیب یه جواب دیگر از معادله به‌دست می‌آید و مقدار آن
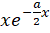است.جواب عمومی معادله دیفرانسیل نیز برابر است با ترکیب خطی این دو:
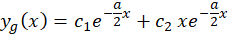
مثال) معادله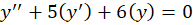 
را حل کنید.
ابتدا معادله مفسر را مشخص و حل می‌کنیم:
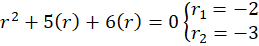
با حالت اول روبرو هستیم پس جواب عمومی برابر است با:
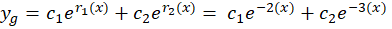
مثال) معادله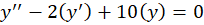
را حل کنید.
ابتدا معادله مفسر را مشخص و حل می‌کنیم:
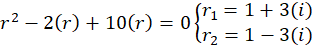
با حالت دوم روبرو هستیم پس جواب عمومی برابر است با:
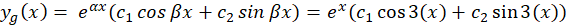
برای تسلط بیشتر بر این مباحث، می‌توانید کپسول آموزشی معادلات دیفرانسیل لینوم را مشاهده کنید.