معادلات خطی ناهمگن مرتبه دوم و بالاتر دارای ضرایب ثابت

در آموزش گذشته، بامعادلات همگن و ناهمگن آشنا شدیم. در این آموزش کپسولی لینوم، قصد داریم به سراغ یادگیریمعادلات خطی ناهمگن مرتبه دوم و بالاتر برویم.

صورت کلی این معادلات به شکل زیر است:

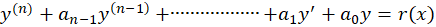
همان طور که مشاهده می‌کنید در این دسته از معادلات ضرایب ثابت هستند.

روش حل معادلات خطی ناهمگن مرتبه دوم و بالاتر دارای ضرایب ثابت

روش حل این معادلات مشابهمعادلات خطی ناهمگن مرتبه دوم و بالاتر دارای ضرایب غیر ثابت است و تنها تفاوت آن در محاسبه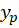 است. اگر ضرایب معادله ثابت باشد و سمت راست معادله یعنی 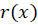برابر با بعضی از توابع خاص باشد می‌توان 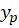را از روش‌هایی که در ادامه به آن‌ها خواهیم پرداخت محاسبه کرد.

روش تعیین ضرایب ثابت

1-اگر 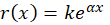 در این حالت جواب خصوصی معادله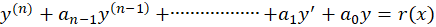

برابر است با:

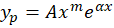
مقدار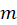 برابر است با تعداد دفعاتی که 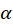ریشهمعادله مفسر بوده‌است. برای به‌دست‌آوردن مقدارA 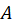هم باید  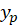را در معادله جایگذاری کنیم.

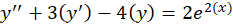مثال) معادله را حل کنید.

ابتدا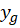 که جواب عمومی معادله همگن شده است را به‌دست می‌آوریم:

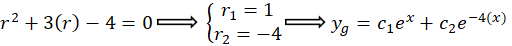
مقدار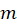 برابر است با تعداد دفعاتی که 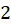ریشه معادله مشخصه است پس 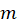برابر با صفر است و فرم کلی 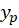به شکل 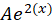است. برای به‌دست‌آوردن مقدار 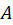هم باید 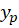را در معادله جایگذاری کنیم:

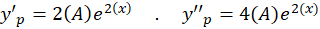
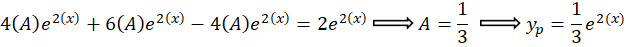
و جواب عمومی معادله برابر است با:

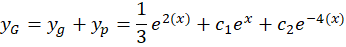
2-اگر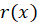 یک چند جمله‌ای از درجه 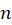به صورت 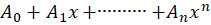باشد، آنگاهجواب خصوصی معادله برابر است با:

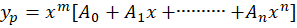
که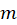 تعداد دفعاتی است که صفر ریشه معادله مشخصه است.

مثال) جواب عمومی معادله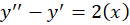 را به‌دست آورید.

ابتدا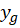 که جواب عمومی معادله همگن شده است، را به‌دست می‌آوریم:

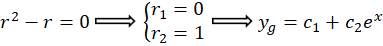
مقدار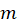 برابر است با تعداد دفعاتی که صفر ریشهمعادله مشخصه است پس برابر با یک است و برای به‌دست آوردن سایر پارامترهای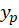 باید آن را در معادله جایگذاری کنیم:

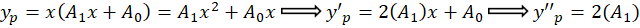
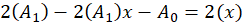
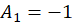
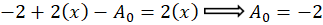
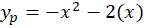
و جواب عمومی این معادله عبارت زیر می‌باشد:

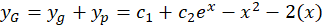
3- اگر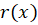 به صورت 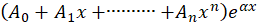باشد، آنگاهجواب خصوصی معادله برابر است با:

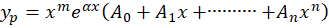
که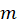 تعداد دفعاتی است که 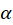ریشه معادله مشخصه است.

مثال) معادله دیفرانسیلy''-7y'+6y=(x-2)ex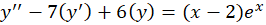 را حل کنید.

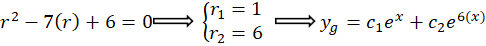
مقدار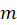 برابر است با تعداد دفعاتی که یک ریشه معادله مشخصه است پس 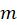برابر با یک است و برای به‌دست‌آوردن سایر پارامترهای 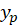باید آن را در معادله جایگذاری کنیم:

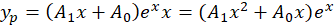
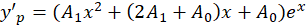
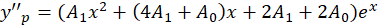
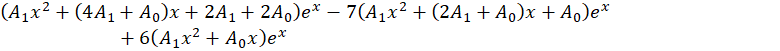
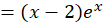
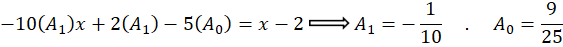
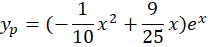
و جواب عمومی این معادله عبارت زیر می‌باشد:

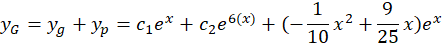
4- اگر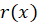 به صورت  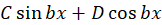باشد، آنگاهجواب خصوصی برابر است با:

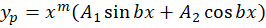
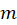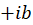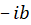مقدار برابر است با تعداد دفعاتی که یا ریشه معادله مشخصه است.

5- اگر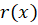 به صورت 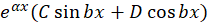باشد، آنگاهجواب خصوصی برابر است با:

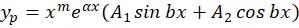
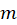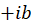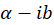مقدار برابر با تعداد دفعاتی است که یا  ریشه معادله مشخصه است.

6-اگر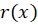 به صورت 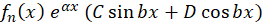باشد که 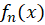یک چند جمله‌ای از درجه 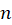است آنگاهجواب خصوصی برابر است با:

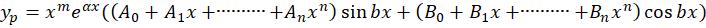
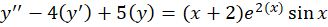مثال) معادله را حل کنید.

ابتدا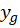 که جواب عمومی معادله همگن شده است را به‌دست می‌آوریم:

و جواب خصوصی نیز به شکل زیر است:

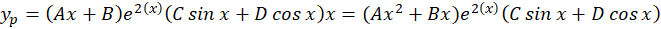
و در نهایت جواب عمومی معادله برابر است با:

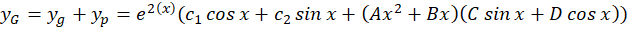
قضیه

اصل برهم نهی جواب های خصوصی

اگر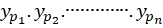 به ترتیبجواب‌های خصوصی معادلات زیر باشند:

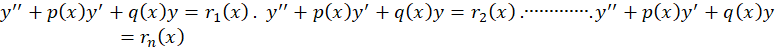
آنگاه جواب خصوصی معادله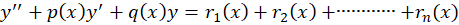 برابر است با:

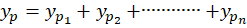
مثال) جواب خصوصی معادله 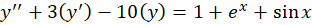 را به‌دست‌آورید.

با توجه به اصل برهم نهی جواب‌های خصوصی ،جواب خصوصی معادله فوق برابر است با جمع جواب‌های خصوصی معادلات زیر:

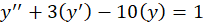
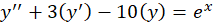
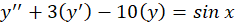
پس به ترتیب جواب خصوصی هر یک از معادلات فوق را تعیین می‌کنیم:

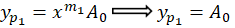
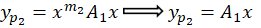
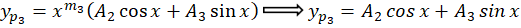
بنابر مطالبی که پیش از این توضیح داده‌بودیم مقدار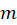در هر سه عبارت صفر به‌دست می‌آید.جواب خصوصی معادله اولیه ما برابر است با:

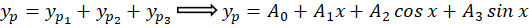
اپراتور معکوس

همان طور که پیش از این در اینآموزش معادلات دیفرانسیل اشاره کرده بویم معادلات خطی ناهمگن مرتبه دوم و بالاتر دارای ضرایب ثابت به دو روش مختلف قابل حل هستند که یکی از آن‌ها حل این معادلات با استفاده ازاپراتور معکوس است.

برای استفاده از روش تعیین ضرایب ثابت حتما می‌بایست سمت راست معادله توابع به خصوصی باشد و در غیر این صورت معادله قابل حل نیست ولی در روش اپراتور معکوس تنها شرطی که به آن نیاز داریم ثابت بودن ضرایب معادله است.

قضایای مرتبط با روش اپراتور معکوس

قبل از بیان قضایا باید بدانیم هر کجا صحبت از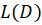 به میان آمد، منظور از آن عبارت زیر است:

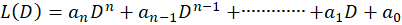
1-با فرض این که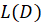 یک عملگر دیفرانسیلی به صورت بالا است داریم:

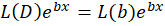
که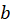 یک عدد ثابت است.

2-فرض کنید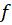 تابعی باشد که حداقل 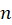بار مشتق پذیر است، آنگاه رابطه زیر برقرار است:

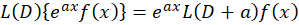
3-اگر منظور از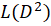 یک عملگر دیفرانسیلی باشد که دارای توان زوج 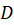است آنگاه داریم:

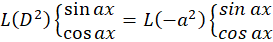
گاهی در نگاه اول توان زوجی وجود ندارد و باید عبارت را به صورت حاصل ضرب عبارت های با توان زوج و توان فرد بنویسید.

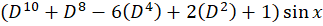مثال) حاصل عبارت را به‌دست‌آورید.

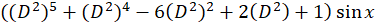
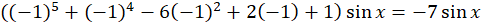
4- فرض کنید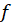 تابعی باشد که حداقل 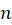بارمشتق‌پذیر است رد این صورت داریم:

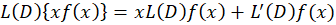
و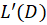 از مشتق گیری 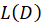 نسبت به 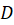به‌دست‌آمده‌است.

5-جواب خصوصی عبارت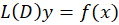 به فرم زیر است:

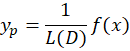
که منظور از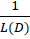 عملانتگرال‌گیری است.با توجه به این که 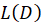را میتوان بر حسب 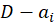 نوشت پس برای محاسبه 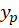، می‌توان رابطه 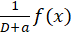 را به کار برد. برای محاسبه حاصل این عبارت می‌توان از دو روش متفاوت استفاده کرد که رد نهایت هر دو خرجی یکسانی را ارائه می‌دهند:

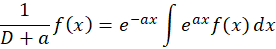
6-در صورتی که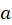 و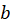 اعداد ثابتی باشند، خاصیت جابجایی برقرار است:

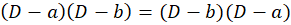
توجه کنید در صورتی که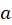 و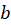 اعداد ثابتی نباشند خاصیت جابجایی به هیچ وجه برقرار نیست.

مثال) جواب معادله دیفرانسیل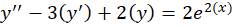  را به‌دست‌آورید.

ابتدا جواب عمومی معادله فوق در حالت همگن شده را به‌دست می‌آوریم:

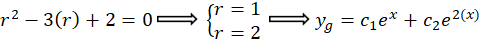
برای به‌دست‌آوردنجواب خصوصی معادله به صورت زیر عمل می‌کنیم:

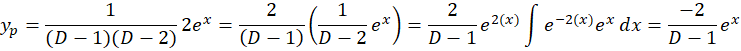
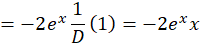
7-با توجه به این که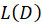 یک عملگر دیفرانسیلی داریم:

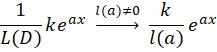
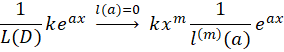
مثال) معادله دیفرانسیل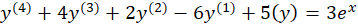 را حل کنید.

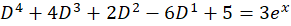
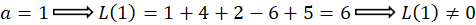
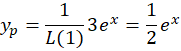
8-با توجه به این که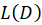 یکعملگر دیفرانسیلی است، داریم:

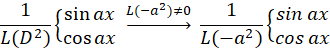
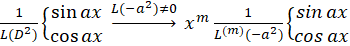
مثال) معادله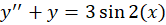 را حل کنید.

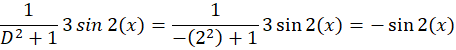
9-اگر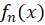 یک چند جمله ای از درجه 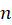باشد، در این صورت:

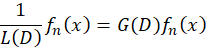
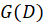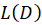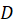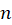که از تقسیم مستقیم یک بر به‌دست می‌آید که تابعی بر حسب خواهد بود.چون یک چند جمله‌ای از درجه است پس کافیست 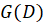را حداکثر تا توان 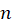به‌دست‌آوریم.

مثال) جواب خصوصی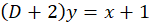 را به‌دست‌آورید.

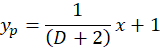
یک را بر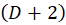 تقسیم کنید. با توجه به این موضوع که یک عبارت درجه اول می‌باشد این کار را تا جایی ادامه دهید که خارج قسمت یک عبارت درجه اول تبدیل شود. با انجام این عمل به خارج قسمت 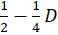خواهید رسید و داریم:

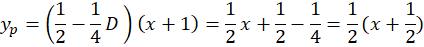
برای تسلط بیشتر بر این مباحث، می‌توانید  کپسول آموزشی معادلات دیفرانسیل لینوم را  مشاهده کنید.